 |
Главная |
Уравнение конвективной диффузии
|
из
5.00
|
Пусть имеется раствор с плотностью растворителя 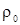 и плотностью растворенного вещества –
и плотностью растворенного вещества – 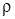 , тогда плотность раствора запишется в виде
, тогда плотность раствора запишется в виде
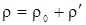
| (2.18) |
Запишем уравнение неразрывности для растворителя:
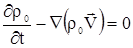
| (2.19) |
Диффузию не учитываем, потому что в жидкостях коэффициент диффузии мал.
Будем считать, что растворитель является несжимаемым, т.е. 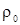 не зависит от пространственных координат и
не зависит от пространственных координат и
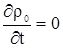
| (2.20) |
Тогда из выражения (2.19), получим
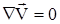
| (2.21) |
Запишем уравнение неразрывности для раствора:
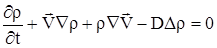
| (2.22) |
В (2.22) подставим (2.18), получим
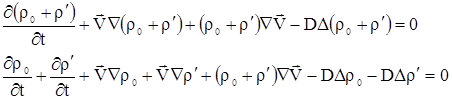
|
Учитывая (2.20), (2.21) и независимость 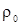 от пространственных координат, получим
от пространственных координат, получим
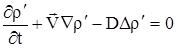
| (2.23) |
Опустим штрих, предполагая в дальнейшем 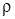 – плотность примеси.
– плотность примеси.
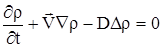
| (2.24) |
Поясним в (2.24) значение каждого слагаемое:
Первое слагаемое 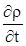 описывает изменение массового содержания в рассматриваемой точке;
описывает изменение массового содержания в рассматриваемой точке;
Второе слагаемое 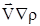 отвечает за конвекцию;
отвечает за конвекцию;
Третье слагаемое 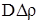 отвечает за диффузию.
отвечает за диффузию.
Физический смысл уравнения (2.24) заключается в следующем: изменение концентрации, со временем, в рассматриваемой точке происходит за счет конвекции и диффузии.
На практике в (2.24) слагаемым 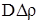 можно пренебречь, в силу его малости.
можно пренебречь, в силу его малости.
Метод характеристик
Пусть движение несущей жидкости происходит вдоль оси 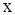 , тогда уравнение без диффузионной конвекции запишется
, тогда уравнение без диффузионной конвекции запишется
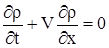 . .
| (1) |
Одномерное уравнение без диффузионной конвекции (или конвекционное уравнение).
Задача Коши для уравнения (1).
Требуется найти функцию 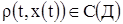 , где
, где 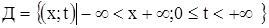 и удовлетворяющую условиям:
и удовлетворяющую условиям:
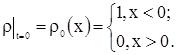
| (2) |
Получим решение задачи методом характеристик.
Метод характеристик заключается в переходе от эйлеровых переменных 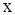 и
и 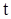 к лагранжевым. Связь производных в эйлеровых и лагранжевых координатах записывается в виде:
к лагранжевым. Связь производных в эйлеровых и лагранжевых координатах записывается в виде:
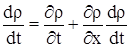 . .
| (3) |
Уравнение (1) таким образом можно записать как систему двух уравнений:
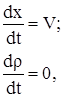
| (4) (5) |
где уравнение (4) – уравнение для характеристик.
Из (5) следует, что 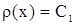 , где
, где 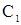 некоторая постоянная. Но т.к.
некоторая постоянная. Но т.к. 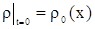 , то
, то 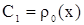 .
.
Из (4) получаем
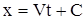 . .
| (6) |
Равенство (6) – решение уравнений характеристик.
Интегральные линии уравнения (4) на мировой плоскости 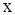 ,
, 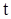 , т.е. графики движения частиц при заданной скорости
, т.е. графики движения частиц при заданной скорости 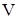 , называются характеристиками уравнения (1).
, называются характеристиками уравнения (1).
Пусть при 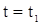 ,
, 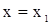 , т.е.
, т.е.
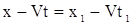 ; ;
| |
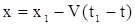 . .
| (7) |
Подставляя (7) в (2), получим
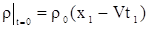 . .
| (8) |
Для того, чтобы получить решение задачи Коши нужно решить систему двух уравнений:
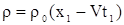 , ,
| (9) |
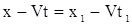 . .
| (10) |
Подставим уравнение (10) в (9), получим
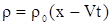 . .
| (11) |
Выражение (11) является решением задачи Коши для уравнения (1).
Решение (11) представляет собой волну бегущую вправо со скоростью 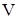 .
.
Начально-краевая задача для уравнения (1) (смешанная задача)
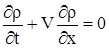 , , 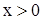 , , 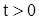 , ,
| (1) |
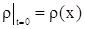 . .
| (2) |
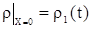 . .
| (3) |
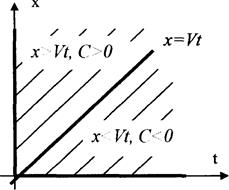
Рис.4.
На рисунке 4 изображены характеристики уравнения (1), где при 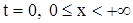 начальное условие, а при
начальное условие, а при 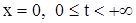 граничное условие,
граничное условие, 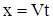 граничная характеристика.
граничная характеристика.
Для задачи Коши решенной ранее,
 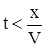  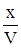
 О О 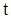 а)
а)
 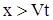
   О О 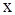 б)
б) 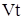 Рис. 5
Рис. 5
| 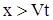 (или (или 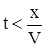 ) (см. рис. 5) и влиять будет только начальное условие ) (см. рис. 5) и влиять будет только начальное условие 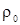 .
Если .
Если 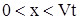 ( ( 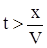 ), то будет влиять только граничное условие ), то будет влиять только граничное условие 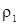 . .
|
Получим решение для граничного решения.
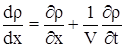
| (5) |
Запишем уравнения (1) в виде
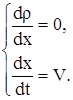
| (6) (7) |
Из (6) следует, что 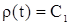 , где
, где 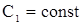 .
.
Учитывая (3) получим 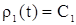 .
.
Интегрируя (7) получаем
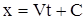 . .
| (8) |
Пусть при 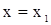 ,
, 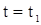 тогда
тогда
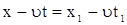
| (9) |
Разделим обе части (9) на 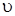 получим
получим
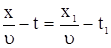 . .
| (10) |
При 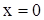 ,
,
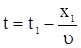 . .
| (11) |
Подставляя (11) в (3) получаем
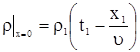 . .
|
Тогда решая систему
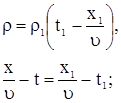
|
получаем решение граничной задачи в виде
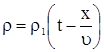 . .
| (12) |
В (12) 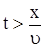 .
.
Решение начально-краевой задачи будет иметь вид
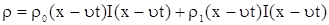 , ,
|
где 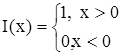 , единичная функция Хевисайда.
, единичная функция Хевисайда.
Решение задачи Коши для неоднородного конвекционного уравнения
Построим формулу Даламбера для уравнения
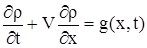 , , 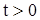 , , 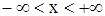
| (1) |
Уравнение (1) – уравнение эволюции локального параметра.
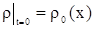 . .
| (2) |
Тогда уравнение (1) запишем в виде системы двух уравнений:
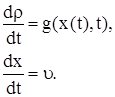
| (3) (4) |
Интегрируя (4), получим
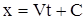
| (5) |
Пусть при 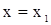 ,
, 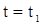 , тогда
, тогда
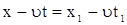 . .
|
Подставим (5) в (3), получим
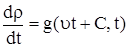 . .
| |
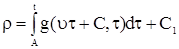 , ,
| (6) |
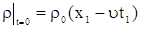 , ,
| (7) |
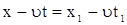 . .
| (8) |
Исключим в (6) 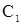 для этого учтем начальное условие (7).
для этого учтем начальное условие (7).
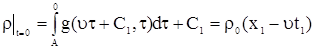 , ,
| |
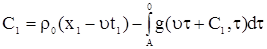 . .
| (9) |
Подставим (9) в (6), получим
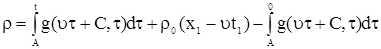 , ,
| |
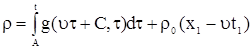 . .
| (10) |
Исключим в (10) 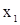 и
и 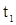 , потом
, потом 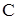 :
:
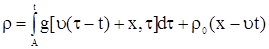 . .
| (11) |
Выражение (11) – формула Даламбера (решение задачи Коши для неоднородного конвекционного уравнения).
Покажем что (11) является решением (1).
Продифференцируем формулу (11) по 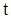 , получим
, получим
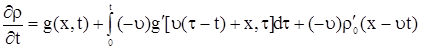 . .
| (12) |
Продифференцируем формулу (11) по 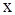 , получим
, получим
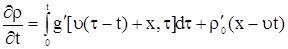 . .
| (13) |
Подставляя (13) и (12) в (1), получаем
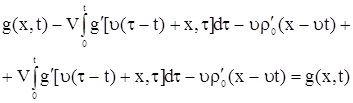 . .
|
Откуда получаем тождество: 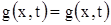 . Следовательно, выражение (11) является решением уравнения (1).
. Следовательно, выражение (11) является решением уравнения (1).
|
из
5.00
|
Обсуждение в статье: Уравнение конвективной диффузии |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

