 |
Главная |
Начально-краевая задача для неоднородного конвективного уравнения
|
из
5.00
|
 , , 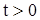 , , 
| (1) |
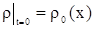 . .
| (2) |
 . .
| (3) |
Найдем решение граничной задачи для неоднородного конвекционного уравнения (1).
Решение будем искать в виде  дифференцируя которое по
дифференцируя которое по  ,получим
,получим
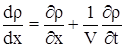 . .
|
Умножая правую и левую части на 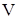 , приходим к выражению
, приходим к выражению
 . .
| (4) |
Перепишем уравнение (1) в виде двух уравнений:

| (5) (6) |
Из (6) следует, что 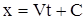 . Пусть при
. Пусть при 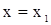 ,
, 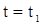 , тогда
, тогда  .
.
Откуда получим
 . .
| (7) |
Подставим уравнение (7) в уравнение (5), получим
 . .
| |
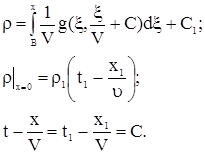
| (8) (9) (10) |
Исключим в (8) 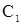 , для этого учтем граничное условие (9).
, для этого учтем граничное условие (9).

| |
 . .
|
Подставим (11) в (8), получим

| (12) |
Исключим в (12) 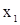 ,
,  и
и  получим
получим
 . .
| |
 , ,
| (13) |
Выражение (13) – формула Даламбера (решение граничной задачи для неоднородного конвекционного уравнения (1)).
Покажем, что (13) является решением (1). Для этого продифференцируем формулу (13) по  , получим
, получим
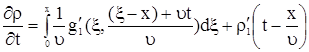 . .
| (14) |
Продифференцируем формулу (13) по  , получим
, получим
 . .
| (15) |
Умножая (15) на  и складывая с (14), получим, после сокращений, что
и складывая с (14), получим, после сокращений, что
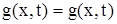
|
то есть, (13) является решением граничной задачи для неоднородного конвекционного уравнения (1).
Решение смешанной задачи запишем, в виде
 . .
|
Слабые растворы
Рассмотрим термодинамические свойства слабых растворов, т. е. таких растворов, в которых число молекул растворенных веществ значительно меньше числа молекул растворителя. Рассмотрим сначала случай раствора с одним растворенным веществом; обобщение для раствора нескольких веществ можно будет произвести непосредственно [1].
Пусть  – число молекул растворителя в растворе, а
– число молекул растворителя в растворе, а  – число молекул растворяемого вещества. Концентрацией раствора назовем отношение
– число молекул растворяемого вещества. Концентрацией раствора назовем отношение  ; согласно сделанному предложению
; согласно сделанному предложению  .
.
Найдем выражение для термодинамического потенциала раствора. Пусть  есть термодинамический потенциал чистого растворителя (в котором ничего не растворено). Согласно формуле
есть термодинамический потенциал чистого растворителя (в котором ничего не растворено). Согласно формуле  (справедливой для чистых веществ) его можно написать в виде,
(справедливой для чистых веществ) его можно написать в виде,
 . .
| (1) |
где  – химический потенциал чистого растворителя. Обозначим посредством
– химический потенциал чистого растворителя. Обозначим посредством  малое изменение, которое испытал бы термодинамический потенциал при введении в растворитель одной молекулы растворяемого вещества. В силу предполагаемой слабости раствора молекулы растворенного вещества в нем находятся на сравнительно больших расстояниях друг от друга, и поэтому их взаимодействие слабо. Пренебрегая этим взаимодействием, можно утверждать, что изменение термодинамического потенциала при введении в растворитель
малое изменение, которое испытал бы термодинамический потенциал при введении в растворитель одной молекулы растворяемого вещества. В силу предполагаемой слабости раствора молекулы растворенного вещества в нем находятся на сравнительно больших расстояниях друг от друга, и поэтому их взаимодействие слабо. Пренебрегая этим взаимодействием, можно утверждать, что изменение термодинамического потенциала при введении в растворитель  молекул растворяемого вещества равно
молекул растворяемого вещества равно  . Однако в получаемом таким путем выражении
. Однако в получаемом таким путем выражении  еще не учтена должным образом одинаковость всех молекул растворенного вещества. Это есть выражение, которое получилось бы по формуле (2), если бы при вычислении статического интеграла все частицы растворенного вещества считались отличными друг от друга. Вычисленный таким образом статический интеграл должен в действительности еще быть поделен на
еще не учтена должным образом одинаковость всех молекул растворенного вещества. Это есть выражение, которое получилось бы по формуле (2), если бы при вычислении статического интеграла все частицы растворенного вещества считались отличными друг от друга. Вычисленный таким образом статический интеграл должен в действительности еще быть поделен на  .
.
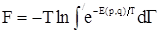 . .
| (2) |
где  – элемент объема фазового пространства, деленный на
– элемент объема фазового пространства, деленный на  :
:
 . .
| (3) |
Это приводит к появлению в свободной энергии, а потому и в потенциале  дополнительного члена
дополнительного члена  . Таким образом,
. Таким образом,
 . .
| (3) |
Далее, поскольку 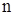 – само по себе очень большое число, хотя и малое по сравнению с
– само по себе очень большое число, хотя и малое по сравнению с  , в последнем члене можно заменить
, в последнем члене можно заменить  . Тогда
. Тогда
 . .
| (3) |
Учтем теперь, что  должно быть однородной функцией первого порядка по отношению к
должно быть однородной функцией первого порядка по отношению к  и
и  . Для этого, очевидно, стоящая под знаком логарифма функция
. Для этого, очевидно, стоящая под знаком логарифма функция  должна иметь вид
должна иметь вид  . Таким образом,
. Таким образом,
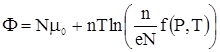 . .
| (3) |
Вводя новую функцию от  и
и  :
:
 , ,
| (3) |
находим окончательно для термодинамического потенциала раствора выражение
 . .
| (8) |
Сделанное в начале этого параграфа предположение относительно прибавления члена вида  к потенциалу чистого растворителя есть в сущности не что иное, как разложение в ряд по степеням
к потенциалу чистого растворителя есть в сущности не что иное, как разложение в ряд по степеням  с оставлением только первых членов. Член следующего порядка по
с оставлением только первых членов. Член следующего порядка по 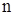 пропорционален
пропорционален  , а с учетом однородности по переменным
, а с учетом однородности по переменным  и
и  должен иметь вид
должен иметь вид  , где
, где  – функция только от
– функция только от  и
и  . Таким образом, с точностью до членов второго порядка термодинамический потенциал слабого раствора имеет вид
. Таким образом, с точностью до членов второго порядка термодинамический потенциал слабого раствора имеет вид
 . .
| (3) |
Обобщение этого выражения на случай раствора нескольких веществ очевидно:
 . .
| (3) |
где  – число молекул различных растворенных веществ.
– число молекул различных растворенных веществ.
Из (8) легко найти химические потенциалы для растворителя (  ) и растворенного вещества (
) и растворенного вещества (  ) в растворе:
) в растворе:
 , ,
| (3) |
 . .
| (12) |
|
из
5.00
|
Обсуждение в статье: Начально-краевая задача для неоднородного конвективного уравнения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

