 |
Главная |
Линейное дифференциальное уравнение первого порядка .
|
из
5.00
|
Определение. Линейным дифференциальным уравнением первого порядка называется уравнение вида y/+g(x)y=h(x).
Такое название ему дано в связи с тем, что относительно переменных y и y/ его можно рассматривать как линейное.
Если  , то уравнение принимает простой вид y/=h(x), и сводится к нахождению неопределенного интеграла
, то уравнение принимает простой вид y/=h(x), и сводится к нахождению неопределенного интеграла  . Его общее решение тогда имеет вид
. Его общее решение тогда имеет вид 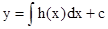 .
.
Если  , то уравнение называется однородным линейным. Оно приобретает вид
, то уравнение называется однородным линейным. Оно приобретает вид  , и, как нетрудно видеть, сводится к решению уравнения с разделяющимися переменными
, и, как нетрудно видеть, сводится к решению уравнения с разделяющимися переменными 
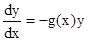 и далее
и далее  .
.
Его общее решение имеет вид 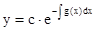 , где
, где  - некоторая первообразная для функции g(x).
- некоторая первообразная для функции g(x).
Предположим теперь, что  , функции g(x) и h(x) являются непрерывными. Пусть y=f(x,c) – искомое общее решение линейного дифференциального уравнения.
, функции g(x) и h(x) являются непрерывными. Пусть y=f(x,c) – искомое общее решение линейного дифференциального уравнения.
Представим исходное уравнение в виде
 ,
,
и подставим в выражение, стоящее в квадратных скобках,  , т.е. как бы полагая в общем решении
, т.е. как бы полагая в общем решении 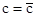 . Тогда вышеприведенное уравнение примет вид
. Тогда вышеприведенное уравнение примет вид
 ,
,
являясь линейным однородным дифференциальным уравнением (в нем вместо y взята для удобства переменная z, чтобы не возникло путаницы решений этого уравнения с исходным).
Общее решение этого уравнения, как уже отмечалось ранее, может быть представлено в виде
 ,
,
где A – произвольная постоянная. Очевидно,  является его частным решением, и, следовательно, может быть получено при некотором значении
является его частным решением, и, следовательно, может быть получено при некотором значении 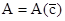 , т.е.
, т.е.
 .
.
Если теперь освободиться от условия фиксирования постоянной 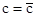 , то получаем, что общее решение исходного уравнения имеет вид
, то получаем, что общее решение исходного уравнения имеет вид
 .
.
В нем второй множитель функция 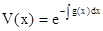 является, как нетрудно видеть, частным решением при c=1 однородного линейного уравнения
является, как нетрудно видеть, частным решением при c=1 однородного линейного уравнения  . Первый множитель функция
. Первый множитель функция  представляет общее решение дифференциального уравнения u/v(x)=h(x).
представляет общее решение дифференциального уравнения u/v(x)=h(x).
Действительно, подставляя в это уравнение u/x(x,c), получаем тождество

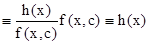 .
.
Таким образом, показано, что общее решение линейного дифференциального уравнения 
Представляется в виде y=u(x,c)v(x), где v(x) – частное решение однородного уравнения  , решаемое при c=1, u(x,c) – общее решение уравнения u/v(x)=h(x).
, решаемое при c=1, u(x,c) – общее решение уравнения u/v(x)=h(x).
Нетрудно видеть, что в обоих случаях приходится решать уравнение с разделяющимися переменными.
Заметим, что хотя при решении однородного уравнения  бралось частное решение V(x) однородного уравнения v/+g(x)v=0,
бралось частное решение V(x) однородного уравнения v/+g(x)v=0,
Являющегося уравнением с разделяющимися переменными.
На втором этапе определяется решение u(x,c) дифференциального уравнения u/v(x)=h(x),
Также являющегося уравнением с разделяющимися переменными. После их решений общее решение исходного линейного уравнения представляется в виде
Y=u(x,c)v(x).
Пример 1. Решить уравнение
Y/+2y=sinx.
Сначала решаем однородное уравнение v/+2v=0.
Из него получаем
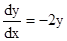 или
или  .
.
Интегрируя его левую и правую части, получаем его общий интеграл (решение) вида
 .
.
Полагая в нем c=0 и потенциируя его, получаем следующее его нетривиальное частное решение  .
.
Далее решаем уравнение вида
 или
или  .
.
Разнося переменные в разные части уравнения и интегрируя их, получаем общее решение этого уравнения
 .
.
Вычислим интеграл:
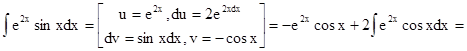
 .
.
Рассматривая данное уравнение, как уравнение относительно интеграла, находим его вид
 .
.
Следовательно, 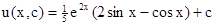 .
.
Тогда общее решение исходного уравнения будет
 .
.
Предположим теперь, что требуется выделить частное решение, проходящее через точку M(0,0), т.е. решение, удовлетворяющее начальному условию y(0)=0. Для этого подставим значения x=0, y=0 в общее решение и найдем соответствующее значение постоянной c:
 , отсюда
, отсюда  .
.
Искомым частным решением является
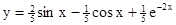 .
.
Пример 2. Решить уравнение
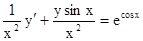 ,
,
являющееся линейным дифференциальным уравнением.
На первом этапе найдем решение соответствующего линейного однородного уравнения
 , или
, или  .
.
Разделяя переменные по разные стороны уравнения, имеем
 .
.
Интегрируя обе части данного уравнения, получаем следующее его частное решение
 .
.
На втором этапе решаем уравнение вида
 .
.
Делая замену  , сокращая обе части уравнения на
, сокращая обе части уравнения на  и разделяя переменные, имеем du=x2dx.
и разделяя переменные, имеем du=x2dx.
Интегрируя правую и левую части уравнения, получаем его общее решение
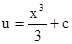 .
.
Общее решение исходного дифференциального уравнения имеет вид
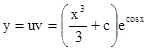 .
.
|
из
5.00
|
Обсуждение в статье: Линейное дифференциальное уравнение первого порядка . |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

