Аффинная система подстановок Цезаря

Аффинная система шифрования относится к классу шифров, основанных на аналитических преобразованиях шифруемых данных. В системе шифрования Цезаря использовались только аддитивные свойства множества целых Z_m, то есть оно рассматривалось как группа с операцией сложения.

Рассматривая множество целых чисел Z_m с двумя операциями сложения и умножения по модулю m, являющееся кольцом, можно получить систему подстановок, которую называют аффинной системой шифрования Цезаря.

Определим в такой системе преобразование Е_a,b: Z_m → Z_m:

 

Е _a,b(x)= ax+b mod m,

 

где в качестве ключа k = (a , b) используется пара целых чисел, удовлетворяющих условиям 0 a,b < m, и НОД(а,m)=1.

В данном преобразовании буква, соответствующая числу x в открытом тексте, заменяется на букву шифртекста, соответствующую числовому значению y =(ax +b) mod m (например m=26 в латинском алфавите).

Следует заметить, что преобразование Е_a,b(x) является взаимно однозначным отображением на множестве Z_m только в том случае, если НОД(а,m)=1, т.е. а и m должны быть взаимно простыми числами.

Это условие взаимной простоты необходимо для обеспечения инъективности отображения Е_a,b(x) = ax+b mod m. Если оно не выполняется, возможна ситуация, когда две разные буквы отображаются в одну (возникает неоднозначность расшифрования), а некоторые буквы отсутствуют в шифртексте, так как никакие буквы в них не отображаются.

Достоинством аффинной системы является удобное управление ключами - ключи шифрования и расшифрования представляются в компактной форме в виде пары чисел (а, b). По сравнению с простой системой шифрования Цезаря, количество возможных ключей значительно больше и алфавитный порядок слов при шифровании не сохраняется.

Аффинная система использовалась на практике несколько веков назад, а сегодня ее применение ограничивается большей частью иллюстрациями основных криптологических положений.

Криптосистема Хилла и её частный случай шифр Плэйфеpа

Эти криптосистемы также относятся к классу шифров, основанных на аналитических преобразованиях шифруемых данных как и аффинная система шифрования. Они основаны на подстановке не отдельных символов, а n - гpамм (шифр Хилла) или 2-гpамм (шифр Плэйфеpа). При более высокой криптостойкости они значительно сложнее для реализации и требуют достаточно большого количества ключевой информации.

Алгебраический метод, обобщающий аффинную подстановку Цезаря для шифрования n-грамм, был сформулирован Лестером С.Хиллом.

Шифрование ведется путем выполнения умножения вектора на матрицу. Матрица является ключом шифрования. Открытый текст разбивается на n-граммы - блоки длиной n, равной размерности матрицы и каждая n-грамма х = (х_0, х_1, х_{2, … ,} х_n-1) рассматривается как вектор.

Ключевая матрица Т размером п×п вида Т={t _i,j}, i,j = 0,1, … ,n-1 задает отображение, являющееся линейным преобразованием:

 

Т: Z_m,n → Z_m,n,    Т: х → у; у=Тх,

 

где .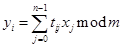

Для расшифрования шифртекста необходимо выполнить обратное преобразование:

 

х = Т^-1 у.

 

Для того, чтобы линейное преобразование Т, заданное своей матрицей, могло быть криптографическим преобразованием необходимо чтобы оно было обратимым (или невырожденным), то есть должна существовать обратная матрица Т^-1: такая, что:

 

Т Т^-1 = Т^-1 Т = I, где I - единичная матрица.

 

Доказано, что для этого необходимо, чтобы определитель матрицы det Т, не делился на любое простое р, которое делит m.

Шифры гаммирования

Суть этого метода состоит в том, что символы шифруемого текста последовательно складываются с символами некоторой специальной последовательности, которая называется гаммой. Такой метод представляют как наложение гаммы на исходный текст, поэтому он получил название «гаммирование».

Гамма шифра - это псевдослучайная последовательность, выработанная по заданному алгоритму для шифрования открытых данных и дешифрования зашифрованных данных. Под гаммированием понимают процесс наложения по определенному закону гаммы шифра на открытые данные, он может выполняться как в режиме блочного, так и потокового шифрования. Он является типичным и наиболее простым примером реализации абсолютно стойкого шифра (при использовании бесконечного ключа п = ).

Процесс шифрования заключается в генерации гаммы шифра и наложении полученной гаммы на исходный открытый текст обратимым образом, например с использованием операции сложения по модулю 2.

Следует отметить, что при блочном шифровании открытые данные разбивают на блоки Т₀⁽ⁱ⁾ одинаковой длины, обычно по 64 бита. Гамма шифра вырабатывается в виде последовательности блоков γ_i аналогичной длины.

Уравнение зашифрования можно записать в виде

 

c_i = γ_i  m_i ,    i=1,…,M,

 

где c _i - i-ый блок шифртекста; γ_i - i-ый блок гаммы шифра; m _i - i-ый блок открытого текста; М - количество блоков открытого текста.

Процесс дешифрования сводится к повторной генерации гаммы шифра и наложению этой гаммы на зашифрованные данные. Уравнение расшифрования имеет вид

 

m_i = γ_i  c_i, i=1,…,M.

 

Полученный зашифрованный текст является достаточно трудным для раскрытия в том случае, если гамма шифра не содержит повторяющихся битовых последовательностей. Криптостойкость определяется размером ключа и методом генерации гаммы.

Чтобы получить линейные последовательности элементов гаммы, длина которых превышает размер шифруемых данных, используются датчики псевдослучайных чисел (ПСЧ). Одним из хороших конгруэнтных генераторов является линейный конгруэнтный датчик ПСЧ. Он вырабатывает последовательности псевдослучайных чисел γ_i, описываемые соотношением

 

γ_{i +1} = (аγ_i + b)mod m,

 

где а и b – константы; γ₀ - исходная величина, выбранная в качестве порождающего числа. Очевидно, что эти три величины и образуют ключ.

Такой датчик генерирует псевдослучайные числа с определенным периодом повторения, зависящим от выбранных значений а и b. Необходимо выбирать числа a и b такие, чтобы период был максимальным. Как показано Д. Кнутом, это возможно тогда и только тогда, когда b - нечетное и взаимно простое с m, и величина а mod 4 = 1. По другим рекомендациям b - взаимно простое с m, и а нечетное.

Процедуру наложения гаммы на исходный текст можно осуществить двумя способами. При первом способе символы исходного текста и гаммы заменяются цифровыми эквивалентами, которые затем складываются по модулю k, где k - число символов в алфавите, т.е.

 

R_i = ( S_i + G ) mod (k –1),

 

 где R_i, S_i, G — символы соответственно зашифрованного, исходного текста и гаммы.

При втором методе символы исходного текста и гаммы представляются в виде двоичного кода, затем соответствующие разряды складываются по модулю 2. Вместо сложения по модулю 2 при гаммировании можно использовать и другие логические операции, например преобразование по правилу логической эквивалентности и неэквивалентности .

Такая замена равносильна введению еще одного ключа, который является выбором правила формирования символов зашифрованного сообщения из символов исходного текста и гаммы (таблица 8).

Таблица 8 - Пример шифрования гаммированием

Шифруемый текст	Б	У	Д	Ь …
	010010	100000	110010	100000
Знаки гаммы	7	1	8	2 …
	000111	000001	001000	000010
Шифрованный текст	010101	1000001	111010	100010

 

Стойкость шифрования методом гаммирования определяется главным образом свойством гаммы - длительностью периода и равномерностью статистических характеристик. Последнее свойство обеспечивает отсутствие закономерностей в появлении различных символов в пределах периода.

Обычно разделяют две разновидности гаммирования - с конечной и бесконечной гаммами. При хороших статистических свойствах гаммы стойкость шифрования определяется только длинной периода гаммы. При этом, если длина периода гаммы превышает длину шифруемого текста, то такой шифр теоретически является абсолютно стойким, т.е. его нельзя вскрыть при помощи статистической обработки зашифрованного текста. Это, однако, не означает, что дешифрование такого текста вообще невозможно: при наличии некоторой дополнительной информации исходный текст может быть частично или полностью восстановлен даже при использовании бесконечной гаммы.

В качестве гаммы может быть использована любая последовательность случайных символов, например, последовательность цифр числа p и т.п. При шифровании с помощью, например, аппаратного шифратора последовательность гаммы может формироваться с помощью датчика псевдослучайных чисел (ПСЧ). В настоящее время разработано несколько алгоритмов работы таких датчиков, которые обеспечивают удовлетворительные характеристики гаммы.

Метод гаммирования становится бессильным, если злоумышленнику становится известен фрагмент исходного текста и соответствующая ему шифрограмма. Простым вычитанием по модулю получается отрезок псевдослучайной последовательности (ПСП) и по нему восстанавливается вся последовательность. Злоумышленники может сделать это на основе догадок о содержании исходного текста. Так, если большинство посылаемых сообщений начинается со слов “СОВ.СЕКРЕТНО”, то криптоанализ всего текста значительно облегчается. Это следует учитывать при создании реальных систем информационной безопасности.

Шифр Вернама

Этот метод является частным случаем шифрования гаммированием для двоичного алфавита (при значении модуля m=2).

Конкретная версия этого шифра, предложенная в 1926 году сотрудником фирмы AT&T Вернамом, использует двоичное представление символов исходного текста. Каждая буква исходного текста в алфавите, расширенном некоторыми дополнительными знаками, сначала переводилась с использованием телеграфного кода Бодо в пятибитовый символ. То есть алфавит криптосистемы представляет собой множество Z₃₂ всех пятибитовых последовательностей.

Ключ k = (k₀ ,k₁ ,...,k _n-1), где "k_i Î Z₃₂ записывался на бумажной ленте. При шифровании ключ добавлялся к исходному тексту суммированием по модулю 2.

В общем случае система шифрования Вернама осуществляет побитовое сложение п -битового открытого текста и п-битового ключа:

 

y_i = x_i  k_i , i =1,…, n

 

Здесь х₁ х₂ ... x_п - открытый текст, k₁ k₂ ... k_п - ключ, y₁ y₂ ... y_п - шифрованный текст.

Расшифрование состоит в сложении по модулю 2 символов у шифртекста с той же последовательностью ключей k:

 

y  k = x.

Метод Вернама использует длинную случайную ключевую последовательность и при его реализации возникают проблемы, связанные с необходимостью передачи ключа.

Полибианский квадрат

Относится к шифрам простой замены, в которых буквы исходного текста заменяются по определенному правилу другими буквами того же алфавита. Одним из первых шифров простой замены считается так называемый полибианский квадрат. За два века до нашей эры греческий полководец и историк Полибий изобрел для целей шифрования квадратную таблицу размером 5х5, заполненную буквами алфавита в случайном порядке.

При шифровании в этом полибианском квадрате находили очередную букву открытого текста и записывали в шифртекст букву, расположенную ниже ее в том же столбце. Если буква текста оказывалась в нижней строке таблицы, то для шифртекста брали самую верхнюю букву из того же столбца. Концепция полибианского квадрата оказалась плодотворной и нашла применение в криптосистемах последующего времени.