Гиперболические уравнения как подкласс дифференциальных уравнений в частных производных. Классификация уравнений в частных производных

Содержание

 

Введение

1. Гиперболические уравнения как подкласс дифференциальных уравнений в частных производных. Классификация уравнений в частных производных

2. Классификация уравнений гиперболического типа в контексте классификации уравнений математической физики

2.1 Волновое уравнение

2.2 Уравнение теплопроводности

2.3 Интегро-дифференциальные уравнения

Применение различных методов решения в зависимости от видов гиперболических уравнений

Явная разностная схема

3.2 Неявная разностная схема

Заключение

Список литературы

 

Введение

 

Настоящая курсовая работа посвящена классификации гиперболических дифференциальных уравнений в частных производных.

Актуальность тематики исследования обусловлена широким кругом практических приложений гиперболических уравнений.

Целью настоящей курсовой работы является приведение классификации гиперболических дифференциальных уравнений в частных производных.

Задачами работы являются:

1. Рассмотреть классификацию гиперболических уравнений в рамках общей классификации уравнений математической физики.

2. Привести собственно классификацию гиперболических дифференциальных уравнений в частных производных.

3. В связи с приведенной классификацией гиперболических дифференциальных уравнений в частных производных описать применение методов решения уравнений.

Изучением дифференциальных уравнений в частных производных занимается математическая физика. Основы теории этих уравнений впервые были изложены в знаменитом «Интегральном исчислении» Л. Эйлера.

Классические уравнения математической физики являются линейными. Особенность линейных уравнений состоит в том, что если U и V – два решения, то функция aU + bV при любых постоянных a и b снова является решением. Это обстоятельство позволяет построить общее решение линейного дифференциального уравнения из фиксированного набора его элементарных решений и упрощает теорию этих уравнений.

Современная общая теория дифференциальных уравнений занимается главным образом линейными уравнениями и специальными классами нелинейных уравнений. Основным методом решения нелинейных дифференциальных уравнений в частных производных выступает численное интегрирование.

Круг вопросов математической физики тесно связан с изучением различных физических процессов. Сюда относятся явления, изучаемые в гидродинамике, теории упругости, электродинамике и т.д. Возникающие при этом математические задачи содержат много общих элементов и составляют предмет математической физики.

Постановка задач математической физики, будучи тесно связанной с изучением физических проблем, имеет свои специфические черты. Так, например, начальная и конечная стадии процесса носят качественно различный характер и требуют применения различных математических методов.

Гиперболические уравнения как подкласс дифференциальных уравнений в частных производных. Классификация уравнений в частных производных

 

Дифференциальные уравнения в частных производных представляют собой одну из наиболее сложных и одновременно интересных задач вычислительной математики. Эти уравнения характеризуются тем, что для их решения не существует единого универсального алгоритма, и большинство задач требует своего собственного особого подхода. Уравнениями в частных производных описывается множество разнообразных физических явлений, и с их помощью можно с успехом моделировать самые сложные явления и процессы (диффузия, гидродинамика, квантовая механика, экология и т. д.).

Дифференциальные уравнения в частных производных требуют нахождения функции не одной, как для ОДУ, а нескольких переменных, например, f (х,у) или f(x,t). Постановка задач включает в себя само уравнение (или систему уравнений), содержащее производные неизвестной функции по различным переменным (частные производные), а также определенное количество краевых условий на границах расчетной области.

Несмотря на то, что Mathcad обладает довольно ограниченными возможностями по отношению к уравнениям в частных производных, в нем имеется несколько встроенных функций. Решать уравнения в частных производных можно и путем непосредственного программирования пользовательских алгоритмов.

Постановка задач для уравнений в частных производных включает определение самого уравнения (или системы нескольких уравнений), а также необходимого количества краевых условий (число и характер задания которых определяются спецификой уравнения). По своему названию уравнения должны содержать частные производные неизвестной функции и (или нескольких функций, если уравнений несколько) по различным аргументам, например, пространственной переменной х и времени t. Соответственно, для решения задачи требуется вычислить функцию нескольких переменных, например, u(x,t) в некоторой области определения аргументов 0<x<L и 0<t<T. Граничные условия определяются как заданные временные зависимости функции и, или производных этой функции, на границах расчетной области 0 и L, а начальные — как заданная и (х, 0).

Сами уравнения в частных производных (несколько условно) можно разделить на три основных типа:

· параболические — содержащие первую производную по одной переменной и вторую — по другой, причем все эти производные входят в уравнение с одинаковым знаком;

· гиперболические— содержащие первую производную по одной переменной и вторую — по другой, входящие в уравнение с разными знаками;

· эллиптические — содержащие только вторые производные, причем одного знака.

Некоторые более сложные уравнения нельзя однозначно подогнать под приведенную классификацию, тогда говорят о гибридных типах уравнений.

Будем использовать в качестве примера очень наглядное и имеющее различные, от очевидных до самых неожиданных, решения уравнение теплопроводности.

Двумерное динамическое уравнение

Рассмотрим следующее параболическое уравнение в частных производных, зависящее от трех переменных — двух пространственных х и у, а также от времени t:

 

 , (1)

Выражение в скобках в правой части уравнения (сумму вторых пространственных производных функции и часто, ради краткости, обозначают при помощи оператора Лапласа: Δu).

Это уравнение называется двумерным уравнением теплопроводности или, по-другому, уравнением диффузии тепла. Оно описывает динамику распределения температуры u(x,y,t) на плоской поверхности (например, на металлической пластине) в зависимости от времени (рис. 1). Физический смысл коэффициента о, который, вообще говоря, может быть функцией как координат, так и самой температуры заключается в задания скорости перетекания тепла от более нагретых областей в менее нагретые. Функция φ(x,y,t,u) описывает приток тепла извне, т. е. источники тепла, которые также могут зависеть как от пространственных координат (что задает локализацию источников), так и от времени и от температуры и.

 

Рис. 1. Физическая модель, описываемая двумерным уравнением теплопроводности

 

Для того чтобы правильно поставить краевую задачу для двумерного уравнения теплопроводности, следует определить следующие дополнительные условия:

· граничные условия, т. е. динамику функции u(x,y,t) и (или) ее производных на границах расчетной области;

· начальное условие, т. е. функцию u(х, у, t).

Если рассматривается не одно уравнение в частных производных, а система уравнений, то соответствующие начальные и граничные условия должны быть поставлены для каждой из неизвестных функций.

Стационарное двумерное уравнение

Частный случай уравнения теплопроводности определяет стационарную, т. е. не зависящую от времени, задачу. Стационарное уравнение описывает физическую картину распределения температуры по пластине, не изменяющуюся с течением времени. Такая картина может возникнуть при условии, что стационарный источник тепла действует довольно продолжительное время, и переходные процессы, вызванные его включением, прекратились. Пример численного решения такого уравнения показан на рис. 2 в виде поверхности u(х,у).

 

Рис. 2. Решение стационарного двумерного уравнения теплопроводности

 

Как несложно увидеть, если искомая функция не зависит от времени, то частная производная по времени в левой части уравнения равна нулю, и само уравнение можно переписать (переобозначив ради упрощения φ<-φ/D) следующим образом:

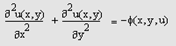(2)

 

Полученное уравнение, согласно классификации предыдущего раздела, является эллиптическим. Его называют уравнением Пуассона, а для его решения в Matcad предусмотрены две встроенные функции. Если, к тому же, источники равны нулю, то уравнение (2), принимающее вид Δu=0, называют уравнением Лапласа.

Одномерное динамическое уравнение

Предположим, что мы рассматриваем задачу распределения тепла не по плоской поверхности, а по удлиненному телу типа металлического стержня (рис. 3). В этом случае зависимость от координаты у в общем уравнении теплопроводности пропадает, и получается одномерное уравнение:

 

(3)

 

Одномерное уравнение намного проще двумерного, поскольку объем вычислений для реализации алгоритма его численного решения не так велик. Типичное решение одномерного уравнения диффузии тепла с коэффициентом диффузии о=2, нулевым источником ф=о и начальным распределением температуры в форме нагретой центральной области стержня показано (в виде графика поверхности) на рис. 3 и 4.

Рис. 3. Физическая модель одномерного уравнения теплопроводности

 

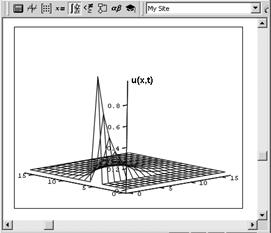
Рис. 4. Решение одномерного уравнения теплопроводности

 

Линейное и нелинейное уравнения

Если присмотреться к уравнению диффузии тепла внимательнее, то можно условно разделить практические случаи его использования на два типа.

· Линейная задача — если коэффициент диффузии о не зависит от температуры и и, кроме того, если источник тепла ф либо также не зависит от и, либо зависит от и линейно. В этом случае неизвестная функция u (x, t) и все ее производные входят в уравнение только в первой степени (линейно).

· Нелинейная задача — если уравнение имеет нелинейную зависимость от u(x,t), т. е. или коэффициент диффузии зависит от и, и (или) источник тепла нелинейно зависит от и.

Решения линейных уравнений в частных производных, как правило, получаются вполне предсказуемыми, и их часто можно получить аналитически (этим проблемам посвящены соответствующие разделы науки, называемой математической физикой). В случае уравнения теплопроводности линейная задача описывает физически ожидаемое решение, выражающее остывание пластины или стержня в форме перетекания тепла от нагретого центра к холодной периферии.

Нелинейные уравнения, напротив, могут демонстрировать самые неожиданные решения, причем в подавляющем большинстве практических задач их можно получить только численно, а никак не аналитически.

Различные линейные и нелинейные варианты рассматриваемого уравнения теплопроводности описывают различные модели физических сред, которые характеризуются определенными зависимостями D(u) и ф(и). В частности, для металлов в большинстве случаев можно считать, что D=const, в то время как для плазмы имеется специфическая зависимость коэффициента диффузии от температуры.

Обратное уравнение теплопроводности

Замечательными свойствами обладает так называемое обратное уравнение диффузии тепла, которое получается путем замены в исходном (прямом) уравнении переменной t на -t. Согласно постановке задачи, обратное уравнение теплопроводности описывает реконструкцию динамики профиля температуры остывающего стержня, если известно начальное условие в виде профиля температуры в некоторый момент времени после начала остывания. Таким образом, требуется определить, как происходило остывание стержня. Мы ограничимся самым простым линейным уравнением с D=const без источников тепла:

 

(4)

Это уравнение гиперболического типа и оно, несмотря на кажущуюся близость к рассмотренным вариантам уравнения теплопроводности, обладает замечательными свойствами.

Если попробовать осуществить расчет обратного уравнения диффузии тепла по тем же самым алгоритмам, что и для обычных, то мы получим заведомо нефизичное решение. Оно показано на рис. 5 в виде профилей распределения температуры для нескольких последовательных моментов времени.

 

Рис. 5. Численное решение обратного уравнения теплопроводности дает совершенно нефизичную картину динамики температуры

 

Как видно, решение выражается в появлении все более быстрых пространственных осцилляции профиля температуры для каждого нового момента времени. Очень существенно, что такое решение является не проявлением неустойчивости численного алгоритма, а определяется спецификой самой задачи.

Оказывается, что обратное уравнение теплопроводности принадлежит к довольно широкому классу задач, называемых некорректными. Некорректные задачи нельзя решать стандартными методами, а для того, чтобы с ними справиться (т. е., чтобы получить осмысленное физическое решение), приходится несколько менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения.