СТАНДАРТИЗАЦИЯ ТЕСТОВЫХ ШКАЛ

Теоретическая справка

Стандартизация тестовых шкал – это создание таких критериев (таблиц), по которым можно будет преобразовывать первичные результаты выполнения теста в относительные оценки.

Например, испытуемый выполнил 16 заданий теста математических достижений из 32 и получил за это 16 баллов из 32 максимально возможных. Таким образом, получается, что он выполнил половину всех заданий, - 50% . Значит ли это, что его достижения можно оценить как СРЕДНИЙ УРОВЕНЬ? Ответ на этот вопрос будет зависеть от того, с чем именно мы будем сравнивать полученный испытуемым результат, с чем будем его соотносить. Если соотносить с максимально возможным баллом, то действительно можно будет сказать, что у испытуемого средний уровень математических достижений. Ну, а сели сравнить с результатами других испытуемых? Например, одинаковых с ним по возрасту, полу, социальному положению и т.п.? Вполне может оказаться, что в этом случае наш испытуемый имеет низкий или высокий уровень достижений. Все будет зависеть от того, сколько еще людей из сравниваемой выборки набрали такие же результаты, сколько - набрали ниже, сколько - набрали выше. Таким образом, во-первых, необходимо иметь данные о результативности выполнения теста определенной выборкой испытуемых, с которой мы будем соотносить наши результаты. А во-вторых, эти данные о результативности мы должны как-то разделить на равные уровни по степени результативности. При этом количество уровней может быть разным – 5 уровней результативности, 9, 10 или 100. И затем, сравнив полученные конкретным испытуемым баллы, мы можем определить его место в той выборке, с которой его соотносим. В данной работе предлагается познакомиться с методами разделения распределения результативности выполнения теста на отдельные уровни.

1.Наиболее простым способом нормирования (разделения распределения на уровни) является шкала процентилей. Процентиль – это точка на числовой шкале, состоящей из 100 уровней. Ранг показателя в процентилях определяется процентным отношением в нормативной группе тех испытуемых, которые получили более низкий показатель. Например, 15 процентиль (Р15)означает, что 15% из нормативной выборки получили показатели ниже данного. Вычисление процентиля немногим сложнее, чем его определение. Оно выражается следующей формулой:

Pp = L + ,

где Pp - искомая величина на шкале процентилей, L - фактическая нижняя граница интервала оценок, содержащего частоту rn, pn - произведение общего количества данных n на относительную частоту (т.е.p/100), f cum - накопленная к L частота, f - частота оценок в интервале, содержащем оценку rn.

Расчет рекомендуется проводить по следующему алгоритму:

а) Упорядочить полученные результаты по возрастанию.

б) Каждому первичному результату приравнять его частоту, т.е.количество испытуемых получивших такой же результат;

в) Произвести накопление частот

г) Подставить значения в формулу.

ПРИМЕР

Преподаватель предложил 125 учащимся контрольное задание, состоящее из 40 вопросов. В качестве оценки теста выбиралось количество вопросов, на которые были получены правильные ответы. Распределение частот различных результатов приводится в таблице № 4. Необходимо определить каков 25-й процентиль в группе 125 оценок, т.е. чему равен Р25. Р25 – это точка, ниже которой лежат 25% 125 оценок.

Таблица № 4.

Оценки по тесту и их частоты.

Вычисление любого процентиля упростится, если построить распределение накопленных частот. Накопленные частоты к любой заданной оценке представляют собой суммарное количество частот на этой оценке и ниже ее. В третьем столбце таблицы указаны накопленные частоты для 125 оценок контрольного задания. Так, например тестовую оценку 33 и меньше получило 106 учащихся.

Вычисление Р25 можно выполнить за 5 шагов:

Шаг 1. r= 0,25, rn = 0,25n =0,25X125 = 31,25

Шаг 2. Найти фактическую нижнюю границу разряда оценок, содержащую испытуемого с оценкой 31,25 снизу: так как 16 человек имеют оценки 28 или меньше, а 34 – оценки 29 или меньше, то частота 31,25 лежит в интервале разряда оценок 28,5- 29,5.

L = 28,5

Шаг 3. Вычесть накопленную к L частоту из 31,25

31,25 – 16 = 15,25

Шаг 4. Разделить результат 3-го шага на частоту f в интервале, содержащем оценку 31,25

= 0,85

Шаг 5. Прибавить результат 4-го шага к L

Р25 = 28,5 + 0,85 = 29,35

Шкала процентилей позволяет оценить отдельный индивидуальный результат относительно других индивидуальных результатов в исследуемой выборке. Самым большим недостатком шкалы процентилей является то, что она не отражает формы первичного распределения результатов. Распределение процентилей всегда равномерно (прямоугольно), тогда как распределение для многих тестов приближается к нормальному и небольшие отклонения от среднего значения сильно увеличиваются процентилями, а относительно большие отклонения, наоборот, сжимаются. Процентили могут таким образом исказить результаты и поэтому их использование не рекомендуется.

2. Наиболее распространенными преобразованиями первичных оценок являются центрирование и нормирование посредством среднеквадратических отклонений (z-преобразование). Под центрированием понимается линейная трансформация величин признака, при которой средняя величина распределения становится равной нулю. Так, если при обследовании группы испытуемых с помощью вновь разрабатываемого теста, средний результат по группе равен 17 «сырых» баллов, то эта величина может быть выбрана в качестве центра отсчета шкалы, в обе стороны от которой симметрично располагаются значения больше и меньше среднего. Для z-преобразования применяется следующая формула:

где 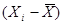- разность между первичным результатом тестового измерения и средней арифметической величиной, - стандартное отклонение для данной выборки.

Неудобство дальнейшей работы со стандартной шкалой состоит в том, что приходится оперировать отрицательными и положительными величинами, а также нулем.

От стандартной z-шкалы легко осуществить переход к любой другой, более удобной шкале. Для этого используется линейное преобразование типа

,

где a>0,0, константы a и b – произвольные действительные числа, выбор которых определяется исключительно удобством дальнейшей работы со шкалой.

В практике психологического тестирования используют ряд так называемых нормализованных шкал: T-шкала, шкала Векслера, шкала Амтхауэра, шкала стенов, шкала станайнов и др.