ОТКРЫТЫЕ СЕТИ С МНОГОРЕЖИМНЫМИ СТРАТЕГИЯМИ ОБСЛУЖИВАНИЯ И ОТРИЦАТЕЛЬНЫМИ ЗАЯВКАМИ

 

Рассматривается открытая сеть массового обслуживания с экспоненциальным обслуживанием в узлах и марковской маршрутизацией, в которую поступают два независимых между собой пуассоновских стационарных потока: обычных (положительных) заявок, требующих обслуживания в узлах, и так называемых отрицательных заявок, которые не обслуживаются и могут удалять из узлов заявки ( 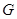-сеть). Положительная заявка после обслуживания может с некоторой вероятностью трансформироваться в отрицательную. Однолинейные узлы могут работать в нескольких режимах, время переключения с одного режима на другой имеет показательное распределение с параметром, зависящим от состояния узла. Переключение происходит только на соседние режимы. Устанавливается условие эргодичности и находится стационарное распределение состояний сети в мультипликативной форме.

Постановка задачи .

В главе 2 рассматривалась открытая сеть с многорежимными стратегиями обслуживания, в которой приборы могут частично выходить из строя, работая при этом в "щадящем" режиме. В 4.1 рассматривается аналогичная сеть при упрощающем предположении, состоящем в том, что интенсивности обслуживания в узле не зависят от его состояния. Однако добавляется возможность поступления в сеть так называемых отрицательных заявок и возможность трансформирования обычных (положительных) заявок в отрицательные, что существенно усложняет задачу, превращая, в частности, линейные уравнения трафика в нелинейные.

В сеть, состоящую из 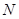 однолинейных узлов, поступают два независимых стационарных пуассоновских потока: положительных заявок с параметром  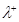и отрицательных заявок с параметром 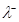. Отрицательные заявки в отличие от обычных (положительных) заявок не требуют обслуживания, а поступление отрицательной заявки в узел уменьшает число заявок в нем на единицу, если число заявок в узле больше нуля, и не производит никаких изменений, если в узле нет заявок. После указанных операций отрицательные заявки исчезают и в дальнейшем не оказывают влияния на сеть. Каждая заявка входного потока положительных заявок независимо от других заявок с вероятностью  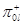направляется в 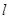-й узел, а каждая заявка входного потока отрицательных заявок независимо от других заявок с вероятностью  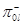направляется в 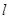-й узел 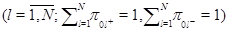. Положительная заявка, обслуженная в 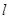-м узле, мгновенно направляется в 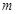-й узел, с вероятностью  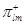оставаясь положительной и с вероятностью  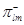превращаясь в отрицательную, или покидает сеть с вероятностью  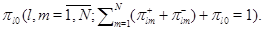В 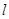-м узле находится единственный прибор, который может работать в  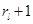режимах. Состояние 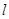-го узла характеризуется парой чисел 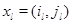, где 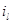 - число положительных заявок в 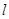-м узле,  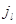- номер режима, в котором работает прибор в 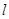-м узле 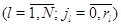. Длительность обслуживания прибором 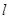-го узла положительных заявок имеет показательное распределение с параметром 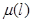. Назовем 0 основным режимом работы. Время пребывания в основном режиме работы имеет показательное распределение с параметром 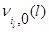, после чего прибор переходит в режим 1. Для состояний 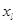, у которых 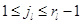, время пребывания в режиме  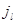также имеет показательное распределение, при этом с интенсивностью  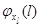прибор 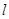-го узла переходит в режим 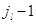, а с интенсивностью  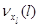- в режим 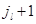. Время пребывания в последнем 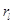-м режиме имеет показательное распределение с параметром 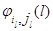, после чего прибор переходит в 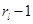-й режим. Во время переключения прибора с одного режима работы на другой число заявок в узле не меняется.

Состояние сети в момент времени 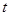 будем характеризовать вектором 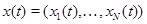, где 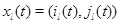 - состояние 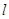-го узла в момент времени 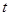. В соответствии с вышесказанным здесь  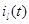- число положительных заявок в 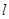-м узле в момент 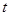,  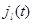- номер режима работы 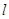-го узла в момент 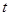. Основная цель данной работы - нахождение стационарного распределения марковского процесса .

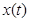Предположим, что все величины 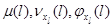 строго положительны. Обозначим через  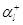среднюю интенсивность поступления положительных заявок в 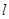-й узел, а через  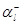среднюю интенсивность поступления отрицательных заявок в 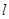-й узел. Эти интенсивности удовлетворяют следующей системе нелинейных уравнений трафика:

 

 

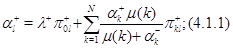
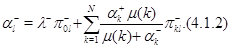
Лемма 1.1 [54, C.91]. Система уравнений (4.1.1), (4.1.2) имеет решение

 

.

 

Доказательство. Так как 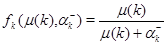 - непрерывная функция от  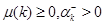и 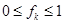, то доказательство следует из результата [90], полученного в этой работе с помощью теоремы Брауэра о неподвижной точке.

В дальнейшем будем предполагать, что существует решение (4.1.1),(4.1.2), для которого все 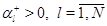. Для того, чтобы это выполнялось, надо наложить некоторые условия на маршрутизацию заявок в сети. Например, такое решение будет заведомо существовать, если при каждом  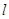выполняется условие 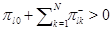. На самом деле можно наложить гораздо менее жесткие условия. Всюду в дальнейшем под словами решение (4.1.1),(4.1.2) будет пониматься именно такое решение. Это предположение гарантирует неприводимость марковского процесса  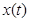на фазовом пространств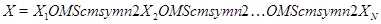е , где .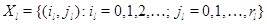

 Изолированный узел в фиктивной окружающей среде .

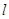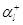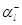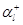Рассмотрим изолированный -й узел в фиктивной окружающей среде, считая, что в него поступают два независимых пуассоновских потока: положительных заявок с параметром  и отрицательных заявок с параметром , где  и 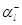 найдены из системы уравнений трафика (4.1.1),(4.1.2). Окружающая среда является фиктивной потому, что в самой сети потоки заявок на ее узлы не являются простейшими. Необходимым и достаточным условием обратимости, а, значит, и квазиобратимости изолированного узла является условие

 

 

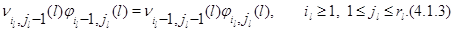
Действительно, модифицируя доказательство леммы 2.2, получаем, что при его выполнении произведение интенсивностей, ведущих из любого состояния в это же самое состояние по ребрам элементарного квадрата по и против часовой стрелки совпадают для марковского процесса, описывающего такой изолированный узел. Условия (4.1.3) выполняются, в частности, если интенсивности переходов из одного режима в другой не зависят от состояния узла. Обозначая через 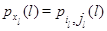 финальные стационарные вероятности его состояний, запишем уравнения обратимости для изолированного узла:

 

 

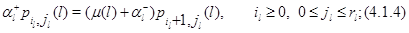
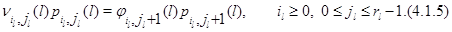
Из этих уравнений легко определяются стационарные вероятности состояний изолированного узла в фиктивной окружающей среде:

 

 

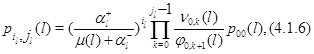
где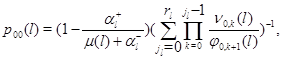

и, как всегда, предполагается, что произведение, в котором нижний индекс больше верхнего, равно 1.

Согласно эргодической теореме Фостера [82] для эргодичности марковского процесса, описывающего изолированный узел в фиктивной окружающей среде, достаточно существования нетривиального неотрицательного решения системы уравнений равновесия такого, что

 

 

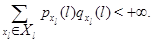
Если

 

 

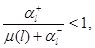
то в силу (4.1.6) ряд 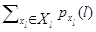 сходится как сумма геометрической прогрессии со знаменателем, меньшим единицы. При выполнении условия

 

 

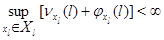
интенсивность выхода из состояния 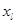 ограничена:

 

 

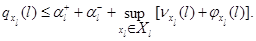
Поэтому при выполнении условий

 

 

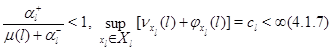
сходится ряд 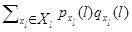 и по эргодической теореме Фостера марковский процесс, описывающий изолированный узел в фиктивной окружающей среде эргодичен.

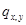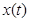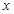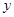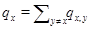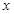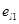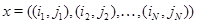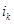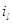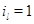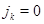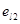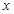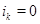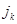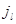 Основной результат . Пусть  - интенсивность перехода процесса  из состояния  в состояние ,  - интенсивность его выхода из состояния ,  - вектор , у которого все  кроме  равны 0, а , и все ,  - вектор , у которого все  и все  кроме  равны 0, а 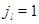. Очевидно, интенсивности перехода процесса  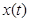имеют следующий вид:

 

 

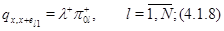
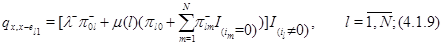
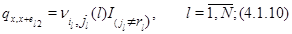
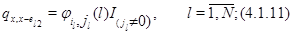
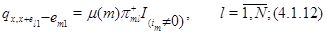
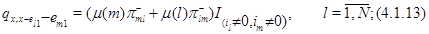
для всех иных состояний  выполняется .

Интенсивность выхода получается сложением этих интенсивностей:

 

 

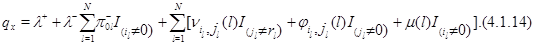
Основной результат 4.1 состоит в следующем.

Теорема 1.1. [54, C.92], [55, C.180] Если для всех 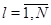 выполняются условия (4.1.3) и неравенства (4.1.7), то марковский процесс  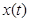эргодичен, а его финальное стационарное распределение имеет форму произведения

 

 

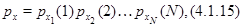
где 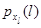 - стационарное распределение изолированного 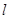-го узла в фиктивной окружающей среде, определяемое с помощью соотношений (4.1.6).

Доказательство. Для доказательства того, что 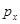, определенные в (4.1.15), образуют стационарное распределение марковского процесса 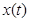, достаточно [94,97,103] подобрать функцию

 

 

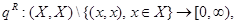
которая удовлетворяла бы соотношениям

 

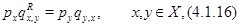
и

 

 

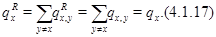
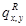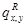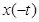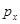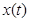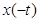Если такие  удастся найти (см. [94,97,103]), то окажется, что  будут являться инфинитезимальными интенсивностями перехода для обращенной во времени цепи Маркова , а  - стационарными вероятностями для  и . Положим

 

 

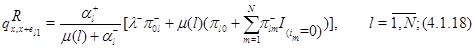
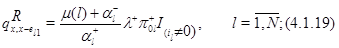
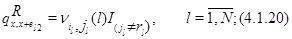
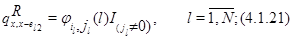
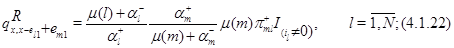
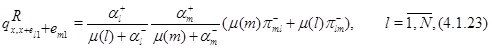
для всех остальных состояний  положим . Для функции 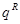 соотношение (4.1.16) действительно выполняется, что легко проверяется подстановкой в него равенств (4.1.8)-(4.1.13), (4.1.18)-(4.1.23) и использования (4.1.4),(4.1.5). Остается доказать (4.1.17). Складывая (4.1.18)-(4.1.23), получим, что

 

 

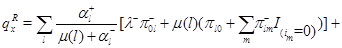
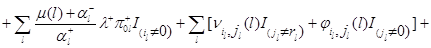
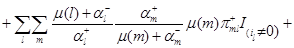
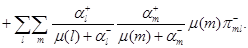
Используя (4.1.1)-(4.1.2), имеем

 

 

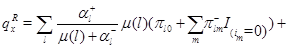
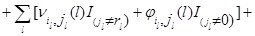
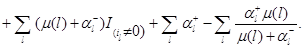
Применяя снова (4.1.1)-(4.1.2), а также свойства индикаторов, получим

 

 

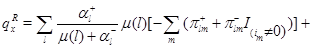
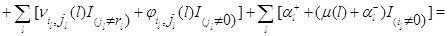
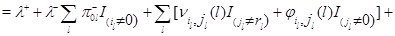
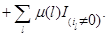
Сравнивая полученный результат с (4.1.14), делаем вывод, что 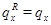 для любого состояния 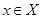. Докажем, что при выполнении условий (4.1.7) марковский процесс  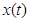эргодичен. Согласно эргодической теореме Фостера [82], для этого достаточно доказать, что существует нетривиальное неотрицательное решение уравнений глобального равновесия

 

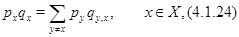
такое, что ряд 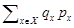 сходится. Складывая (4.1.16) по всем 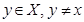, убеждаемся, что  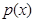является решением (4.1.24). Из (4.1.14) следует, что

 

 

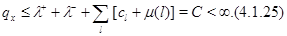
Поскольку ряд

 

 

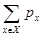
распадается в произведение 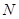 рядов, каждый из которых сходится в силу условия (4.1.7) как сумма бесконечной геометрической прогрессии со знаменателем, меньшим единицы, то и сам он сходится. В силу (4.1.25) будет сходиться ряд

 

 

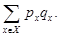
По эргодической теореме Фостера это означает, что марковский процесс 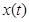 эргодичен. Таким образом, теорема доказана полностью.

Замечание 4.1. Если условия (4.1.3) и (4.1.7) выполнены во всех узлах, то получается простой алгоритм для нахождения стационарных вероятностей:

1. Проверяется выполнение условий (4.1.3).

2. Решается система нелинейных уравнений (4.1.1)-(4.1.2).

3. Проверяется выполнение (4.1.7).

4. Определяются 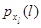 с помощью соотношений (4.1.6).

5. Находится стационарное распределение состояний сети 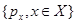 с помощью формулы (4.1.15).

Этот алгоритм может быть дополнен алгоритмом расчета совместного стационарного распределения чисел заявок в узлах и совместного стационарного распределения номеров режимов работы узлов, а также расчета моментов этих распределений. Если 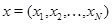 - состояние сети, где 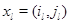, то через  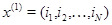обозначим вектор, характеризующий числа положитнльных заявок в узлах, а через  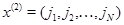- вектор, характеризующий режимы работы в узлах. Стационарные распределения этих двух векторов обозначим соответственно  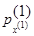и .

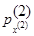Нетрудно убедиться, складывая (4.1.15) по всем возможным значениям 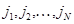, что совместное стационарное распределение чисел положительных заявок в узлах имеет следующую форму:

 

 

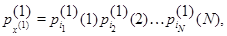
где каждый множитель имеет геометрическое распределение

 

 

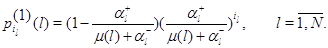
Производящая функция стационарного распределения числа заявок в 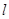-м узле имеет вид

 

 

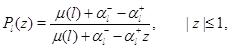
а 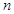-й факториальный момент есть

 

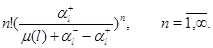
Как и следовало ожидать, в стационарном режиме среднее число положительных заявок и дисперсия числа положительных заявок в каждом узле,

 

 

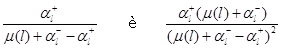
стремятся к нулю, когда загрузка этого узла

 

 

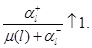
Точно так же, складывая (4.1.15) по всем возможным значениям 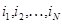, определим совместное стационарное распределение режимов в узлах сети:

 

 

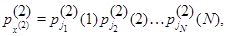
где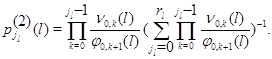

 

Средний номер режима работы 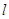-го узла в стационарной сети находится как

 

 

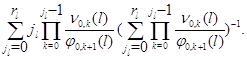
Анализ характера выходящих потоков из сети провести крайне трудно, так как эти потоки являются сложными благодаря воздействию отрицательных заявок и из-за нелинейности уравнений трафика.