Докажите, что предел суммы двух функций равен сумме их пределов, если последние существуют.

(несовсем с функциями связано, но то же свойство, вроде, может подойдет, что-то другого ничего нету)

Пусть a и b – соответственно пределы {Xn} и {Yn}. Тогда Xn = a + αn, Yn = b + βn, где {αn} и {βn} – бм послед-и. Следовательно, (Xn±Yn) – (a±b) = αn ± βn.

Послед-ь {αn ± βn} – бм. Таким образом, послед-ь {(Xn±Yn) – (a±b)} также бм и поэтому послед-ь (Xn±Yn) сходится и имеет своим пределом число a±b.

16. Докажите, что функция f(x) = sin 1/x не имеет предела в точке x = 0.

lim (x→0) sin 1/x по Гейне lim (n→∞) Xn = X0, lim(x→0+0) 1/x = +∞, lim(x→0-0) 1/x = - ∞

lim (x→0+0) sin 1/x – не сущ. sin (x→0-0) 1/x – не сущ.

17. Может ли функция f(x) +g(x) быть непрерывной в точке х0, если функция f(x) непрерывна, а функция g(x) имеет разрыв в этой точке, а функция g(x)имеет разрыв в этой точке. ответ обоснуйте.

Нет. Так как есть теорема, в которой говорится. Если f(x) и g(x)- непрерывные функции в точке x0, то непрерывными являются .

.f(x)=c-является непрерывной и f(x)=x.

18 Найдите значение а, при котором функция f(x) = x arctg (1/x), x≠0, является непрерывной в точке x=0.

lim (x→ x0) f(x) = f(x0)

является непрерывной в точке x = 0

 следовательно

 следовательно а=0

22. Функция y = f (x), определенная в некоторой окрестности точки х₀ , называется непрерывной в этой точке, если предел функции в точке х₀ существует и равен значению в этой точке: lim _{х → х0} f(x) = f(x₀).

Функция y = f ( x ) называется непрерывной в точке х = х₀ , если эта функция определена в какой-либо окрестности точки х₀ и в самой точке х₀ , и если бесконечно малому изменению аргумента соответствует бесконечно малое изменение функции.

23.Теорема о непрерывности сложной ф-ции. 

Сложная функция, составленная из конечного числа суперпозиций непрерывных функций, тоже непрерывная функция.

24. Теорема о непрерывности обратной ф-ции. Функция обратная для монотонной и непрерывной функции также непрерывна.

25. Теорема о непрерывности элементарных ф-ций. Любая элементарная функция непрерывна в своей области определения. (Промежутки непрерывности элементарных функций точно совпадают с их областью определения).

26. Точка х₀ называется точкой разрыва функции f(x), если или не существует.

Разрыв 1 рода (скачок) если в этой точке функция имеет конечные, но не равные друг другу левый и правый пределы.

Разрыв 2 рода (бесконечный), если в этой точке функция f(x) не имеет по крайней мере одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.

Разрыв 3 рода (устранимый), если функция не существует в точке х₀  или если значение функции в точке х₀ не совпадает со значением односторонних пределов.

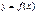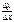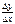27.определение производной в точке Пусть функция  определена в некоторой окрестности точки x₀(∆x=x-x₀). Производной функции  в точке x₀ называется lim , когда  (при условии, что lim существует). Обозначение .

28. Если функция y = f(x) имеет производную в точке х₀ , то мы говорим, что функция дифференцируема в этой точке.

29. Дифференциалом функции в точке х₀ называется линейная относительно приращения аргумента часть приращения функции в этой точке, эквивалентная всему приращению.

df(х₀)= f ′ (х₀) ∆х;       ∆х=dх; df(х₀)= f ′ (х₀) dх