Прямоугольная система координат

Прежде чем приступить к созданию первой управляющей программы вы должны вспомнить, что такое прямоугольная система координат. Ведь именно прямоугольная система координат служит математической базой программирования обработки. Более 300 лет назад французский математик Декарт придумал систему, которая позволяет человеку описать положение любой точки в пространстве. В простейшем случае прямоугольная система координат представляет собой две пересекающиеся под прямым углом линии. Эти линии называются осями, а точка их пересечения является началом координат.

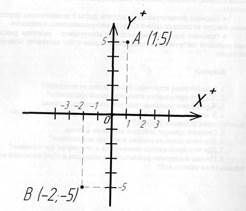
Рис. 1. Прямоугольная система координат на плоскости.

Оси обозначаются буквами X и Y. Координатная система с двумя осями X и Y позволяет описать положение точки на плоскости. Расстояние от начала координат до точки А вдоль оси X, является (х) координатой этой точки. Расстояние от начала координат до точки А вдоль оси Y, является (y) координатой этой точки. Координаты точки принято указывать в скобках. Сначала пишется координата по оси X, а затем по оси Y. Таким образом на рисунке 1 находится точка А(1;5).

У каждой оси есть положительное и отрицательное направление. Когда координата имеет отрицательное значение, то это означает, что точка лежит либо левее начала координат, либо ниже. Например, точка В имеет следующие координаты: х= -2, у= -5. Если точка лежит на какой-либо оси, то одна из ее координат обязательно равна нулю.

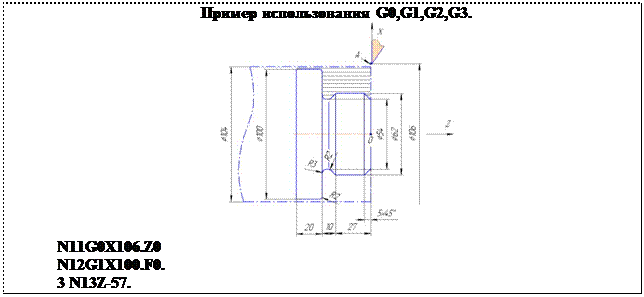
Применительно к токарной обработке прямоугольная система координат будет выглядеть следующим образом.

Рис. 2. Помещаем обрабатываемую деталь в прямоугольную систему координат.

Помещаем обрабатываемую деталь в прямоугольную систему координат таким образом, чтобы ось детали совпала с осью Z, как показано на рисунке, а ось Х расположилась на правой плоскости детали.

Считаем, что резец будет перемещаться в плоскости чертежа: по оси Х – поперечное точение, по оси Z – продольное точение. До обработки заготовка имеет цилиндрическую форму больше максимального диаметра. Если бы можно было изготовить эту деталь за один проход, то траекторию движения инструмента (резца) мы описали бы следующим образом:

Вначале, чтобы подрезать торец, мы установили бы резец его вершиной Е в точку с координатами X=84.0 Z=0^*)

 

*)При программировании в абсолютных координатах (т.е. от выбранных на рисунке осей X и Z) Х – значение диаметра, на котором расположена точка, Z – действительная координата по оси Z.

Затем на ускоренном ходу переводим его в точку “1”, однако при этом поцарапается только что обработанная плоскость. Чтобы этого не произошло, отведем чуть-чуть(например на 0.5мм) резец от обработанной плоскости, а уже затем в положение Х=40. Таким образом, вершина резца окажется в точке Х=40. Z=0.5 Далее, чтобы получить заданный чертежом контур, перемещаем резец со скоростью рабочей подачи в точку ”1”, затем последовательно в точки ”2”, ”3”, ”4”. Дальнейшая обработка данным резцом невозможна. Поэтому выводим его из обработки (со скоростью рабочей подачи) в точку Х=86. Z=-50. После чего возвращаем в референтную позицию (где можно менять инструмент).

Для продолжения обработки вызываем следующий инструмент – отрезной резец. Помещаем его на ускоренной подаче в исходную точку (для него это точка X=86. Z=-50.) Затем включаем скорость рабочей подачи (отрезного резца) и перемещаем резец в точку “5”. Произойдет отрезка готовой детали.

Команды интерполяции.

Для перемещения режущего инструмента вдоль обрабатываемого контура в системе программирования ISO-7 bit используются команды интерполяции. Это линейная интерполяция G01 (G1) и круговая интерполяция G02 (G2) или G03 (G3) соответственно по часовой или против часовой стрелки. Формат следующий. Для линейной интерполяции:

G1 X(диаметр)Z(координата)F(значение подачи) – в абсолютных координатах

G1 U(приращение)W(приращение)F(значение подачи) – в относительных координатах (иначе: в инкрементных значениях или в приращениях)

Команда G0, хотя и очень похожа на G1 интерполяцией не является, т.к. под интерполяцией понимается точный расчет всех точек траектории движения, а для G0 такой расчет система управления не производит. Главное – конечная точка, координаты которой и указываются в команде ускоренного перемещения, а путь следования в эту точку обычно не оговаривается. Если необходимо, можно оговорить последовательность перемещения, например: сначала по Z, а потом по Х. Для этого координаты по Z и по Х надо записать в разных кадрах (в разных строках).

N11 G0 Z25. N12       X15.

При программировании линейной интерполяции имеется в виду перемещение из последней описанной точки (она должна быть описана до вступления в работу данной команды) в точку, координаты которой даются в текущей команде. Т.е. инструмент находился в точке X15.Z25., далее следует команда:

N13 G1 X20.Z30.F500

Следовательно, далее инструмент проследует по прямой, соединяющей точки X15.Z25. и X20.Z30. Если в следующем кадре написать Х10., то инструмент, достигнув точки X20.Z30., проследует далее в точку Х10.Z30., и т.д. мы можем описывать траекторию движения инструмента, если она состоит из отрезков прямой линии.

Можно описать те же самые перемещения в инкрементном выражении (иначе: в относительной системе координат):

N11G0Z25. N12X15.

N13U5.W5.F500 N14U-10.

Если нам нужно описать перемещение инструмента по радиусу, мы прибегаем к использованию команд круговой интерполяции. Направление радиуса по или против часовой стрелки определяем, поместив мысленно инструмент в текущую точку на чертеже обрабатываемой детали с той стороны, откуда будет обработка на станке. Программирование сводится после указания нужного G-кода (по или против ч.стр.) к указанию координат конечной точки радиуса (X…, Z…) и указанию величины самого радиуса, которое можно осуществить двумя путями: 1) указать R… 2) указать координаты центра радиуса в инкрементном выражении (в приращениях) относительно точки начала радиуса I…, K….

Ограничения при круговой интерполяции.

1. Если дуга задается первым способом (с помощью радиуса R), нельзя задать дугу 180° и более в одном кадре (либо за несколько кадров, либо через инкрементные I, K).

2. Если одновременно задать I, K, R, то будет использоваться дуга, заданная радиусом R, а остальные данные будут проигнорированы.

3. Если задается ось, не содержащаяся в данной плоскости, высвечивается сигнал тревоги.

4. Если в результате ваших неправильных расчетов вы указали, как конечную точку радиуса, точку, не лежащую на радиусе, система высвечивает сигнал тревоги.