Линейные и квадратные уравнения , содержащие параметр

Знакомство с параметром.

С параметрами учащиеся встречаются при введении некоторых понятий. Не приводя подробных определений, рассмотрим в качестве примеров следующие объекты:

    - функция прямая пропорциональность: y = kx (x и y – переменные; k – параметр, k 0);

    - линейная функция: y = kx + b (x и y – переменные, k и b – параметры);

    - линейное уравнение: ax + b=0 (x – переменная; a и b – параметры);

    - уравнение первой степени: ax + b=0 (x – переменная; a и b – параметры, а 0);

    - квадратное уравнение: ax²+b х+с=0 (х – переменная; а, b и с – параметры, а 0).

    Основное, что нужно усвоить при первом знакомстве с параметром, – это необходимость осторожного, даже, если хотите, деликатного обращения с фиксированным, но неизвестным числом.

    Необходимость аккуратного обращения с параметром хорошо видна на тех примерах, где замена параметра числом делает задачу банальной. К таким задачам, например, относятся: сравнить два числа, решить линейное или квадратное уравнение, неравенство и т.д.

    В ЕГЭ выделяется класс задач, где за счет параметра на переменную накладываются какие-либо искусственные ограничения. Для таких задач характерны следующие формулировки: при каком значении параметра уравнение (неравенство, система) имеет одно решение, два, бесконечно много, ни одного; решением уравнения (неравенства, системы) является какое-то подмножество множества действительных чисел и др.

Основные виды уравнений, содержащих параметр

Линейные и квадратные уравнения , содержащие параметр

Линейные и квадратные уравнения, содержащие параметр, можно объединить в одну группу – группу уравнений с параметром не выше второй степени.

Уравнения с параметром не выше второй степени являются самыми распространенными в практике итоговых и конкурсных заданий. Их общий вид определяется многочленом . Для таких уравнений всякое частное уравнение не выше второй степени принадлежит одному из следующих типов:

1. 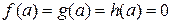, тогда ,

2.  и , тогда решений нет,

3.  и , тогда ,

4. , , тогда ,

5. , , тогда решений нет,

6. , , тогда .

Контрольные значения параметра определяются уравнением . На выделенных контрольными значениями промежутках допустимых значений параметра дискриминант имеет определенный знак, соответствующие частные уравнения принадлежат одному из двух последних типов.

Тогда решением всякого уравнения с параметром не выше второй степени осуществляется по следующим этапам:

1. На числовой прямой отмечаются все контрольные значения параметра, для которых соответствующие частные уравнения не определены.

2. На области допустимых значений параметра исходного уравнения при помощи равносильных преобразований приводится к виду .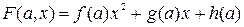

3. Выделяют множество контрольных значений параметра, для которых .

   Если уравнение  имеет конечное множество решений, то для каждого найденного контрольного значения параметра соответствующее частное уравнение решается отдельно. Проводится классификация частных уравнений по первым трем типам.

    На бесконечном множестве решений уравнения  проводится решение уравнения , выделяются типы бесконечных и пустых особых частных уравнений. Множеству значений параметра, для которых  и , соответствует третий тип не особых частных уравнений.

4. Выделяются контрольные значения параметра, для которых дискриминант обращается в нуль. Соответствующие не особые частные уравнения имеют двукратный корень .

5. Найденные контрольные значения параметра разбивают область допустимых значений параметра на промежутки. На каждом из промежутков определяется знак дискриминанта.

    Множеству значений параметра, для которых  и , соответствует тип не особых частных уравнений, не имеющих решений, для значений параметра из множества, где  и , частные уравнения имеют два различных действительных корня.

    Пример. Решить уравнение

.                                   (1)

Решение . Здесь контрольными будут те значения параметра, при которых коэффициент при х обращается в 0. Такими значениями являются, а=0и а=2. При этих значениях параметра а, невозможно деление обеих частей уравнения на коэффициент при х. В то же время при значениях параметра а≠0 и а≠2 деление возможно. Таким образом, целесообразно множество всех действительных значений параметра разбить на подмножества

A₁={0}, А₂={2} и А₃= {а≠0, а≠2}

и решить уравнение (1) на каждом из этих подмножеств, т. е. решить уравнение (1) как семейство уравнений, получающихся из него при следующих значениях параметра: 1) а=0; 2) а=2; 3) а≠0, а≠2.

    Рассмотрим эти случаи.

1) При а=0уравнение (1) принимает вид 0∙х=2. Это уравнение не имеет корней.

2) При а=2уравнение (1) принимает вид 0∙х=0. Корнем этого уравнения является любое действительное число.

3) При а≠0, а≠2 уравнение соответствует третьему типу откуда
х = = .

0твет : 1) если а=0, то корней нет;

2) если а=2, то х — любое действительное число;

3) если а≠0, а≠2 , то х = .

    Пример. Решить уравнение

.             (2)

Решение . В данном случае контрольным значением параметра a является единица. Дело в том, что при a=1 уравнение (2) является линейным, а при а≠1 оно квадратное (в этом и состоит качественное изменение уравнения). Значит, целесообразно рассмотреть уравнение (2) как семейство уравнений, получающихся из него при следующих значениях параметра: 1) a=1; 2) а≠1.

Рассмотрим эти случаи.

1) При a=1 уравнение (2) примет вид 6х+7=0. Из этого уравнения находим х = – .

2) Из множества значений параметра а≠1 выделим те значения, при которых дискриминант уравнения (2) обращается в 0.

Дело в том, что если дискриминант D=0при а=а_о,то при переходе значения D через точку а_одискриминант может изменить знак (например, при а<а_о D < 0, а при а>а_о D > 0). Вместе с этим при переходе через точку а_о меняется и число действительных корней квадратного уравнения (в нашем примере при а<а_окорней нет, так как D < 0, а при а>а_о D > 0 уравнение имеет два корня). Значит, можно говорить о качественном изменении уравнения. Поэтому значения параметра, при которых обращается в 0 дискриминант квадратного уравнения, также относят к контрольным значениям.

Составим дискриминант уравнения (2):

. После упрощений получаем .

Из уравнения =0 находим 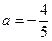 — второе контрольное значение параметра а. При этом если , то D < 0; если , то D ≥ 0; и .

Таким образом, осталось решить уравнение (2) в случае, когда  и в случае, когда  и .

Если , то уравнение (2) не имеет действительных корней;

если же  и , то находим ;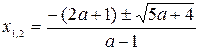

если , то  и тогда .

Ответ : 1) если , то корней нет;

2) если а = 1, то х = ;

3) если , то ;

4) если , то .