 |
Главная |
Основные методы решения уравнений , содержащих параметр
|
из
5.00
|
Аналитический метод
В самом начале знакомства с параметром у учеников возникает некий психологический барьер, который обусловлен противоречивыми характеристиками параметра. С одной стороны, параметр в уравнении следует считать величиной известной, а с другой – он может принимать различные значения. Получается, что параметр в уравнении – это неизвестная известная, переменная постоянная величина. Этот «каламбур» очень точно отражает существо тех сложностей, которые нужно преодолевать ученикам.
Именно этот факт и позволяет нам решать уравнения с параметром таким методом («ветвления»)
Пример. Решить уравнение 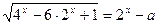 .
.
Решение. Пусть  . Тогда
. Тогда 
Переходим к равносильной системе

Очевидно, при  уравнение системы не имеет решения.
уравнение системы не имеет решения.
Если  , то тогда
, то тогда

Следовательно, нужно проверить условия  и
и 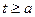 . То есть
. То есть

решая из системы первое неравенство, получаем что  .
.
Решением второго есть  . Решением системы будет пересечение интервалов, а, именно,
. Решением системы будет пересечение интервалов, а, именно,  .
.
Ответ . Если  , то
, то  ;
;
при остальных значениях параметра a уравнение решений не имеет.
Выделим класс задач, где за счет параметра на переменную накладывается какие-либо ограничения. Именно такие задачи встречаются в составе ЕГЭ (задания С5). Для таких задач характерны следующие формулировки:
· «При каком значении параметра уравнение имеет одно решение, два решения, бесконечно много, ни одного»;
· Решением уравнения (неравенства, системы) является какое-то подмножество множества действительных чисел и другие.
Пример.В зависимости от значения параметра  найти число корней уравнения
найти число корней уравнения

Решение. Наличие сложного корня наводит на мысль выделения квадрата двучлена под внешним корнем.

Итак, мы вплотную подошли к задаче рассмотрения различных случаев параметра  .
.
Если  , то уравнение не имеет решения.
, то уравнение не имеет решения.
Если  , то рассмотрим
, то рассмотрим  . Если
. Если  , то
, то  . При условии
. При условии  , и очевидно это уравнение имеет только один корень.
, и очевидно это уравнение имеет только один корень.
Ответ . При  – одно решение,
– одно решение,
при  – решений нет.
– решений нет.
Пример . При каких значениях параметра  уравнение
уравнение
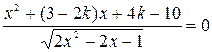
имеет единственное решение?
Решение . Уравнение переписываем в равносильную систему

Решением неравенства является объединение промежутков  . Уравнение системы имеет один корень когда
. Уравнение системы имеет один корень когда  .
.  , то есть при
, то есть при 
 .
.
Теперь проверим, принадлежит ли корень нашим интервалам:  .Тогда
.Тогда
Ответ . При  уравнение имеет единственное решение.
уравнение имеет единственное решение.
Пример. При каких значениях параметра  уравнение
уравнение
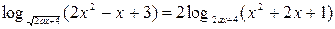 .
.
имеет единственное решение?
Решение . Запишем равносильное уравнение.
 .
.
Теперь перейдем к следствию  . Откуда
. Откуда  ,
,  . Возникла ситуация, которая дает нам возможность воспользоваться механизмом отсеивания корней.
. Возникла ситуация, которая дает нам возможность воспользоваться механизмом отсеивания корней.
Область определения исходного уравнения найдем из условий

Очевидно, 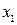 и
и  удовлетворяют первым двум условиям. Тогда для единственности решения достаточно потребовать
удовлетворяют первым двум условиям. Тогда для единственности решения достаточно потребовать

Найдем решение первой системы, преобразуем ее.

Имеем, что решением первой системы является объединение интервалов  .
.
Вторая система решения не имеет.
Ответ .  .
.
Параметр и свойства решений уравнений, содержащих параметр
В этом пункте мы рассмотрим задачи, в которых условие требует, чтобы ответ был каким-либо наперед заданным подмножеством или идут ограничения на множество значений переменной  .
.
Пример. При каких значениях параметра  оба корня уравнения
оба корня уравнения  больше 3?
больше 3?
Решение . Корнями данного уравнения будут

Для условия необходимо выполнение системы

Первое неравенство системы и второе будут иметь общие точки только в том случае если выражение под корнем равно нулю.
Решим уравнение  .
.
Ответ. Ни при каких значениях параметра  оба корня данного уравнения не могут быть больше 3.
оба корня данного уравнения не могут быть больше 3.
Параметр как равноправная переменная
Во всех разобранных задач параметр рассматривался как фиксированное, но неизвестное число. Между тем с формальной точки зрения параметр – это переменная, причем равноправная с другими. Подобная интерпретация, естественно, формирует еще один тип (а точнее метод решения) задач с параметрами.
Пример. Указать все значения параметра  , для которых уравнение
, для которых уравнение 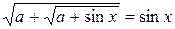 имеет решение?
имеет решение?
Решение . Обозначим  . Исходное уравнение
. Исходное уравнение 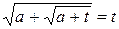 , с учетом
, с учетом  , равносильно системе
, равносильно системе

Рассмотрим квадратное уравнение, относительно параметра 
 . Найдем дискриминант рассматриваемого уравнения
. Найдем дискриминант рассматриваемого уравнения  .
.
 , так как
, так как  и
и  , то
, то  . Поэтому последняя система равносильна
. Поэтому последняя система равносильна 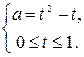
Рассмотрим функцию 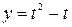 . Вершина параболы – есть точка с координатами
. Вершина параболы – есть точка с координатами  . Минимум функции есть значение ординаты вершины параболы. Поэтому можем утверждать, что параметр
. Минимум функции есть значение ординаты вершины параболы. Поэтому можем утверждать, что параметр  принимает значения в отрезке
принимает значения в отрезке  на отрезке
на отрезке  .
.
Ответ . 
Пример . Решить уравнение  .
.
Важно показать при изучении параметров связь параметра с конкретными значениями и эта задача показывает эту связь. Цель этой задачи в том, чтобы показать что задачи, не содержащие параметр, можно решать и способами решения уравнений, содержащих параметр. Решение этого уравнения показывает, что исследования различных решений с параметрами позволяет решать задачи более простыми методами.
Решение. Это уравнение равносильно системе

Представим уравнение системы в виде квадратного уравнения относительно числа 5.

Откуда, учитывая  , получаем
, получаем
Ответ .  .
.
«Каркас» квадратичной функции. Дискриминант, старший коэффициент.
Фактически все важные свойства квадратичной функции определяются таблицей. Где  – конструируют «каркас», на котором строится теория квадратичной функции
– конструируют «каркас», на котором строится теория квадратичной функции

| 
| 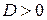
| |||||||

|

| 
|
 
| ||||||

|
 
| 
|

|
Пример. При каких значениях параметра  все пары чисел
все пары чисел  , удовлетворяющие неравенству
, удовлетворяющие неравенству  , одновременно удовлетворяют и
, одновременно удовлетворяют и  ?
?
Решение. Часто бывает удобно начать решение задачи с рассмотрения упрощенной модели. Так, в конкретном случае уместно поставить задачу: при каком соотношении  и
и  все решения неравенства
все решения неравенства 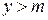 одновременно являются решениями неравенства
одновременно являются решениями неравенства  . Ответом на этот вопрос очевиден:
. Ответом на этот вопрос очевиден:  .
.
Тогда в этом примере нужно, чтобы  при всех
при всех  .
.
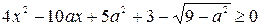 .
.
Найдем дискриминант,  . Дискриминант меньший либо равный нулю определит искомый параметр.
. Дискриминант меньший либо равный нулю определит искомый параметр.
 , что равносильно системе
, что равносильно системе



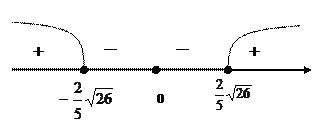

Ответ. 
«Каркас» квадратичной функции. Вершина параболы
Пример. При каких значениях  наибольшее значение трехчлена
наибольшее значение трехчлена 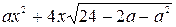 меньше 4.
меньше 4.
Решение.
a. Так как графиком трехчлена является парабола, то необходимость наибольшего значения меньшего 4 обязывает параметр  .
.
b. Наибольшее значение будет в вершине параболы.
 . Ограничение
. Ограничение 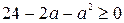 тоже обязательно. Решением этого неравенства есть
тоже обязательно. Решением этого неравенства есть  . Учитывая необходимость
. Учитывая необходимость  , то
, то 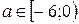 .
.

так как  , то решением будет объединение
, то решением будет объединение  .
.
Тогда Ответ.  .
.
Корни квадратичной функции. Теорема Виета
Рассмотрим квадратное уравнение  . Найдем корни этого уравнения
. Найдем корни этого уравнения  . По теореме Виета выполняется следующая система уравнений
. По теореме Виета выполняется следующая система уравнений  , где
, где  и
и  . Рассмотрим задачу, решение которой при использовании теоремы Виета намного упрощается.
. Рассмотрим задачу, решение которой при использовании теоремы Виета намного упрощается.
Пример. При каком значении параметра  сумма квадратов корней уравнения
сумма квадратов корней уравнения  принимает наименьшее значение?
принимает наименьшее значение?
Решение. Найдем дискриминант,  . Уравнение имеет два корня при любом
. Уравнение имеет два корня при любом  . Используя теорему Виета, найдем
. Используя теорему Виета, найдем 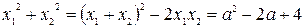 . Таким образом, найдем наименьшее значение функции
. Таким образом, найдем наименьшее значение функции  на множестве
на множестве  . Поскольку при
. Поскольку при 
 , а при
, а при 
 , то наименьшее значение при
, то наименьшее значение при  .
.
Ответ.  .
.
Пример. Найти критические точки функции  .
.
Решение . Напомним определение критической точки. Внутренняя точка области определения функции, в которой производная равна 0 или не существует, называется критической.
Имеем 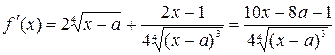 . Поскольку найденная производная существует во всех внутренних точках области определения функции
. Поскольку найденная производная существует во всех внутренних точках области определения функции 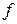 , то критические точки следует искать среди корней уравнения
, то критические точки следует искать среди корней уравнения  , откуда
, откуда  . Осталось потребовать, чтобы
. Осталось потребовать, чтобы  .
.
Ответ . Если  , то
, то  - критическая точка;
- критическая точка;
если  - критических точек нет.
- критических точек нет.
Функциональный подход
Учащиеся не всегда умеют сознательно использовать информацию о свойствах функций, например, о ее множестве значений, непрерывности, экстремумах и так далее.
Многие школьники лишь формально усваивают понятие производной, не понимают ее геометрического смысла. Есть проблемы и при изучении понятий первообразной и интеграла. Задачи, которые приведены ниже, призваны пояснить школьнику смысл всех этих понятий и показать возможности их применения.
Предложенные задачи классифицированы в зависимости от того, какое свойство функции является основным в решении.
Область значения функции
Иногда задачи не содержат прямой подсказки использовать область значения функции. Такая необходимость возникает в ходе решения.
Пример . Решить уравнение  .
.
Решение. Так как  , то пусть
, то пусть 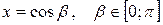 . Получаем
. Получаем 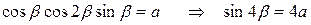 . Очевидно, при
. Очевидно, при  решение имеется. Найдем корни
решение имеется. Найдем корни  , так как
, так как  , то рассмотрим три случая:
, то рассмотрим три случая:
1.  , тогда
, тогда 
2.  ,
, 
3.  ,
, 
Ответ . Если  , то
, то  ;
;
если  , то
, то  ;
;
если  , то
, то  .
.
Пример.Решить уравнение  .
.
Решение . Рассмотрим область допустимых значений  . Отсюда
. Отсюда  ,
,  . Тогда получаем равносильное уравнение
. Тогда получаем равносильное уравнение
 .
.
Откуда  . Учтем два случая, так как
. Учтем два случая, так как  , то
, то  .
.
1.  . Тогда
. Тогда  .
.
2.  . При
. При 
 , а
, а  . Этот случай мы рассмотрели. Тогда рассмотрим случай
. Этот случай мы рассмотрели. Тогда рассмотрим случай  . Откуда
. Откуда  . Итак,
. Итак,
Ответ . Если  решений нет;
решений нет;
если  ,
,  ;
;
если  ,
,  .
.
Наибольшее и наименьшее значени я
При решении задач весьма полезным оказывается следующее обстоятельство. Если в уравнении  , где
, где  ,
,  , а
, а  для всех
для всех  , то можно перейти к равносильной системе уравнений
, то можно перейти к равносильной системе уравнений 
Пример. Решить уравнение
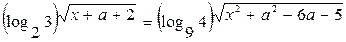 .
.
Решение . Произведем преобразование правой части.  . Тогда наше уравнение будет иметь вид
. Тогда наше уравнение будет иметь вид  .
.
Оценим левую и правую части уравнения  . Тогда заключаем, что обе части уравнения должны быть равны единице и это нас приводит к системе
. Тогда заключаем, что обе части уравнения должны быть равны единице и это нас приводит к системе 
Запишем равносильную систему 
Выразим х из первого уравнения системы и подставим во второе уравнение.

Решением последней системы будут  и
и  .
.
Тогда Ответ. Если  , то
, то 
Если  , то
, то  .
.
Пример. Найти все значения параметра  , при каждом из которых уравнение
, при каждом из которых уравнение  имеет ровно 8 решений.
имеет ровно 8 решений.
 Решение . Имеем
Решение . Имеем  . Рассмотрим функцию
. Рассмотрим функцию  . Первая из них задает семейство полуокружностей с центром в точке с координатами
. Первая из них задает семейство полуокружностей с центром в точке с координатами  , второе семейство прямых параллельных оси абсцисс.
, второе семейство прямых параллельных оси абсцисс.
Число корней будет соответствовать числу 8 тогда, когда радиус полуокружности будет больше  и меньше
и меньше  , то есть
, то есть  . Заметим, что
. Заметим, что  есть
есть  .
.
Ответ . 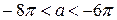 или
или  .
.
Графический метод. Координатная плоскость ( x ; a )
Вообще, уравнения, содержащие параметр, не обеспечены какой-либо четкой, методически оформленной системой решения. Те или иные значения параметра приходится искать на ощупь, перебором, решая большое количество промежуточных уравнений. Такой подход далеко не всегда обеспечивает успех в отыскании всех значений параметра, при которых уравнение не имеет решений, имеет одно, два и более решений. Зачастую часть значений параметра теряются или появляются лишние значения. Для того чтобы эти последние, приходится проводить специальное исследование которое может оказаться довольно трудным.
Рассмотрим метод, упрощающий работу по решению уравнений с параметром. Метод состоит в следующем
· Из уравнения с переменной x и параметра a выразим параметр как функцию от x:  .
.
· В координатной плоскости xOa строим график функции  .
.
· Рассмотрим прямые  и выделим те промежутки оси Oa, на которых эти прямые удовлетворяют следующим условиям: a) не пересекает график функции
и выделим те промежутки оси Oa, на которых эти прямые удовлетворяют следующим условиям: a) не пересекает график функции  , б) пересекает график функции
, б) пересекает график функции  в одной точке, в) в двух точках, г) в трех точках и так далее.
в одной точке, в) в двух точках, г) в трех точках и так далее.
· Если поставлена задача найти значения x, то выражаем x через a для каждого из найденных промежутков значения a в отдельности.
Взгляд на параметр как на равноправную переменную находит свое отражение в графических методах. Таким образом, возникает координатная плоскость  . Казалось бы, такая незначительная деталь, как отказ от традиционного обозначения координатной плоскости буквами x и y определяет один из эффективнейших методов решения задач с параметрами.
. Казалось бы, такая незначительная деталь, как отказ от традиционного обозначения координатной плоскости буквами x и y определяет один из эффективнейших методов решения задач с параметрами.
Описанный метод очень нагляден. Кроме того, в нем находят применение почти все основные понятия курса алгебры и начал анализа. Задействуется весь набор знаний, связанных с исследованием функции: применение производной к определению точек экстремума, нахождение предела функции, асимптот и т. д.
 Пример . При каких значениях параметра
Пример . При каких значениях параметра  уравнение
уравнение 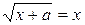 имеет два корня?
имеет два корня?
Решение . Переходим к равносильной системе 
 .
.
Из графика видно, что при 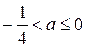 уравнение имеет 2 корня.
уравнение имеет 2 корня.
 Ответ . При
Ответ . При 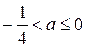 уравнение имеет два корня.
уравнение имеет два корня.
Пример . Найдите множество всех чисел  , для каждого из которых уравнение
, для каждого из которых уравнение 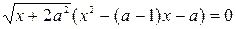 имеет только два различных корня.
имеет только два различных корня.
Решение . Перепишем данное уравнение в следующем виде:

Теперь важно не упустить, что  ,
,  и
и  – корни исходного уравнения лишь при условии
– корни исходного уравнения лишь при условии  . Обратим внимание на то, что график удобнее строить на координатной плоскости
. Обратим внимание на то, что график удобнее строить на координатной плоскости  . На рисунке 3 искомый график – объединение сплошных линий. Здесь ответ «считывается» вертикальными прямыми.
. На рисунке 3 искомый график – объединение сплошных линий. Здесь ответ «считывается» вертикальными прямыми.
Ответ . При  , или
, или  , или
, или  .
.
|
из
5.00
|
Обсуждение в статье: Основные методы решения уравнений , содержащих параметр |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

