 |
Главная |
Геометрическая интерпретация комплексных чисел. Длина отрезка
|
из
5.00
|
Введение
Большое значение комплексных чисел в математике и ее приложениях широко известно. Особенно часто применяются функции комплексного переменного. Их изучение имеет самостоятельный интерес.Вместе с тем алгебру комплексных чисел можно успешно использовать в элементарной геометрии, тригонометрии, теории геометрических преобразований, а также в электротехнике и различных задачах с механическим и физическим содержанием.
Метод комплексных чисел позволяет решать планиметрические задачи по готовым формулам прямым вычислением, элементарными выкладками. Выбор этих формул с очевидностью диктуется условиями задачии ее требованием. В этом состоит необычайная простота этого метода по сравнению с координатным,векторным и другими методами, требующими от решающего порой немалой сообразительности, длительных поисков, хотя готовое решение может быть очень коротким.
В данной работе излагаются основы метода комплексных чисел в применении к задачам элементарной геометриина плоскости и доказательству некоторых основных планиметрических теорем.
Конечно, одна работа не может вместить все существующие теоремы и задачи. Здесь будут рассмотрены лишь некоторые темы, по каждой из которых будет решен ряд задач, наиболее наглядно показывающих простоту этого метода.
Геометрическая интерпретация комплексных чисел. Длина отрезка
При заданной прямоугольной декартовой системе координат на плоскости комплексному числу z = x+iy (i2= -1) можно взаимно однозначно поставить в соответствие точку М плоскости с координатами х, у (рис.1):
 .
.
| |
Число z тогда называют комплексной координатой точки М.
Поскольку множество точек евклидовой плоскости находитсяво взаимно однозначном соответствии с множеством комплексных чисел, то эту плоскость называют также плоскостью комплексных чисел. Начало О декартовой системы координат называют при этом начальнойили нулевой точкой плоскости комплексных чисел.
При у=0 число z действительное. Действительные числа изображаются точками оси х, поэтому она называется действительной осью. При х=0 число z чисто мнимое: z = iy . Мнимые числа изображаются точками оси у, поэтому она называется мнимой осью. Нуль - одновременно действительное и чисто мнимое число.
Paccтoяниe от начала О плоскости до точки М(z) называется модулем комплексного числа z и обозначается | z | или r:
|z| = r = |OM| =  .
.
Если  — ориентированный угол, образованный вектором
— ориентированный угол, образованный вектором  с осью х, то по определению функции синуса и косинуса
с осью х, то по определению функции синуса и косинуса

откуда  и поэтому
и поэтому  .
.
Такое представление комплексного числа z называется его тригонометрической формой. Исходное представление z = x + iy называют алгебраической формой этого числа. При тригонометрическом представлении угол  называют аргументом комплексного числа и обозначают еще через arg z :
называют аргументом комплексного числа и обозначают еще через arg z :
 .
.
Если дано комплексное число z = x + iy , то число  называется комплексно-сопряженным (или просто сопряженным) этому числу z. Тогда, очевидно, и число z сопряжено числу
называется комплексно-сопряженным (или просто сопряженным) этому числу z. Тогда, очевидно, и число z сопряжено числу  . Точки М(z) и
. Точки М(z) и  симметричны относительно оси х (рис.2).
симметричны относительно оси х (рис.2).
Из равенства  следует y=0 и обратно. Это значит, что число, равное своему сопряженному, является действительным и обратно.
следует y=0 и обратно. Это значит, что число, равное своему сопряженному, является действительным и обратно.

Точки с комплексными координатами z и -z симметричны относительно начальной точки О. Точки с комплексными координатами z и  симметричны относительно оси у. Из равенства z =
симметричны относительно оси у. Из равенства z =  вытекает x =0 и обратно. Поэтому условие z =
вытекает x =0 и обратно. Поэтому условие z =  является критерием чисто мнимого числа.
является критерием чисто мнимого числа.
Для любого числа z, очевидно, |z | = |  | = |- z | = |
| = |- z | = |  |.
|.
Сумма и произведение двух сопряженных комплексных чисел являются действительными числами:  .
.
Число, сопряженное с суммой, произведением или же частным комплексных чисел, есть соответственно сумма, произведение или же частное чисел, сопряженных данным комплексным числам:
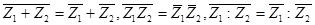
Эти равенства можно легко проверить, пользуясь формулами для операций над комплексными числами.
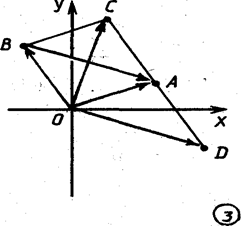
Каждой точке М( z ) плоскости - взаимно однозначно соответствует вектор  . Поэтому комплексные числа можно интерпретировать векторами, приложенными к точке O. Сложению и вычитанию комплексных чисел отвечает сложение и вычитание соответствующих им векторов. Именно если а и b - комплексные координаты точек A и В соответственно, то число с=а+ b является координатой точки С, такой, что
. Поэтому комплексные числа можно интерпретировать векторами, приложенными к точке O. Сложению и вычитанию комплексных чисел отвечает сложение и вычитание соответствующих им векторов. Именно если а и b - комплексные координаты точек A и В соответственно, то число с=а+ b является координатой точки С, такой, что  (рис.3). Комплексному числу d = a - b соответствует такая точка D , что
(рис.3). Комплексному числу d = a - b соответствует такая точка D , что 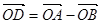 .
.
Расстояние между точками А и В равно  :
:
|АВ| = |а- b |. (1)
Так как | z |2= z 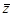 , то
, то
| AB | 2 =(a-b)(  ). (2)
). (2)
Уравнение z 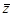 = r 2 определяет окружность с центром О радиуса r. Отношение
= r 2 определяет окружность с центром О радиуса r. Отношение  , в котором точка С делит данный отрезок АВ, выражается через комплексные координаты этих точек так:
, в котором точка С делит данный отрезок АВ, выражается через комплексные координаты этих точек так:

откуда 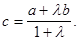 (3)
(3)
Если положить 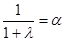 и
и 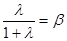 , то
, то
 (4)
(4)
Условия (4) необходимы и достаточны для того, чтобы точки А, В, С были коллинеарны.
При  точка С является серединой отрезка AB, и обратно.
точка С является серединой отрезка AB, и обратно.
Тогда:
c =  . (4a)
. (4a)
Пусть имеем параллелограмм ABCD . Его центр имеет комплексную координату  =
= 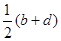 при условии, что точки А, В, С, D имеют соответственно комплексные координаты а, b , с, d . Если не исключать случай вырождения параллелограмма, когда все его вершины оказываются на одной прямой, то равенство
при условии, что точки А, В, С, D имеют соответственно комплексные координаты а, b , с, d . Если не исключать случай вырождения параллелограмма, когда все его вершины оказываются на одной прямой, то равенство
a+c = b+d (5)
является необходимым и достаточным условием того, чтобы четырехугольник ABCD был параллелограммом.
Задача 1. Точки М и N — середины диагоналей АС и BD четырехугольника ABCD. (Рис.1)
Доказать, что |AB|2+|BC|2+|CD|2+|DA|2 = |AC|2+|BD|2+4| MN |2.
Решение. Пусть точкам A, В, С, D, М, N соответствуют комплексные числа а, b , с, d, т, п.
Так как m =  и n =
и n = 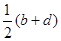 , то
, то
|AB|2+|BC|2+|CD|2+|DA|2 

|AC|2+|BD|2+4|MN|2 

 .
.
Равенство доказано.
Задача 2. Доказать, что если в плоскости параллелограмма ABCD существует такая точка М, что |MA|2+|MC|2=|MB|2+|MD|2, тo ABCD - прямоугольник. (Рис.2)
Решение. Если за начальную точку принять центр параллелограмма ABCD, то при принятых ранее обозначениях с= - a , d = - b , и поэтому данное в условии равенство будет эквивалентно равенству  , которое означает, что диагонали параллелограмма равны, т. е. он прямоугольник.
, которое означает, что диагонали параллелограмма равны, т. е. он прямоугольник.
Задача 3. Доказать, что сумма квадратов диагоналей AC, BD четырехугольника ABCD равна удвоенной сумме квадратов отрезков MN , PQ , соединяющих середины противоположных сторон . (Рис.3)



C
B B C
 | |||
 | |||

 N M MЬ
N M MЬ

 A D A D
A D A D
Рис. 1 Рис. 2
 | |||
 | |||
Решение. Требуется доказать: 
Запишем левую часть равенства в комплексной форме:  . Воспользовавшись (4a), находим комплексное равенство правой части и непосредственным подсчетом убеждаемся, что она равна левой.
. Воспользовавшись (4a), находим комплексное равенство правой части и непосредственным подсчетом убеждаемся, что она равна левой.

B


 P
P


 C
C
M 

N
 A
A
Q D
Рис. 3
Задача 4. Доказать, что сумма квадратов медиан BM , AN , CP треугольника ABC равна  суммы квадратов его сторон. (Рис.4)
суммы квадратов его сторон. (Рис.4)
Решение. Требуется доказать:  Запишем левую часть, воспользовавшись формулами (2) и (4а), и убедимся в том, что она равна правой.
Запишем левую часть, воспользовавшись формулами (2) и (4а), и убедимся в том, что она равна правой.
Задача 5. Доказать, что расстояние от вершины С треугольника АВС до точки D, симметричной центру описанной окружности относительно прямой АВ, вычисляется по формуле |CD|2=R2+|AC|2+|BC|2-|AB|2, где R -радиус описанной окружности. (Рис.5)
Решение. Точка M является серединой АВ, так как центр описанной окружности лежит на пересечении серединных перпендикуляров.
Точка М - середина О D (по условию).
Тогда,  . Воспользуемся этим равенством, формулами (2) и (4а) и убедимся в справедливости |CD|2=R2+|AC|2+|BC|2-|AB|2.
. Воспользуемся этим равенством, формулами (2) и (4а) и убедимся в справедливости |CD|2=R2+|AC|2+|BC|2-|AB|2.




|
 | |||
 | |||

 N
N

 P
P
 A
A
 |
C
A M C
Рис. 4 Рис. 5
Параллельность и перпендикулярность. Коллинеарность трех точек
ОПР: Пусть на плоскости комплексных чисел даны точки А(а) и B(b). Векторы  и
и  сонаправлены тогда и только тогда, когда arg a = arg b, т. е. при arg а - arg b = arg
сонаправлены тогда и только тогда, когда arg a = arg b, т. е. при arg а - arg b = arg 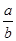 =0 (при вычитании комплексных чисел, из аргумента делимого вычитается аргумент делителя!).
=0 (при вычитании комплексных чисел, из аргумента делимого вычитается аргумент делителя!).
Очевидно также, что эти векторы направлены противоположно в том и только в том случае, если arg a - arg b=arg  .
.
Комплексные числа с аргументами 0, 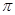 ,
,  являются действительными. ТЕОРЕМА (Критерий коллинеарности точек О, А, В): Для того чтобы точки А(а) и В( b ) были коллинеарны с начальной точкой О, необходимо и достаточно, чтобы частное
являются действительными. ТЕОРЕМА (Критерий коллинеарности точек О, А, В): Для того чтобы точки А(а) и В( b ) были коллинеарны с начальной точкой О, необходимо и достаточно, чтобы частное 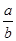 было действительным числом, т. е.
было действительным числом, т. е.
 или
или  (6)
(6)
Действительно, так как в этом случае число 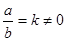 действительное ( k =
действительное ( k =  ), то критерий (6) эквивалентен такому:
), то критерий (6) эквивалентен такому:
 . (7)
. (7)
Возьмем теперь точки A(а), B(b), C(c), D(d).
ОПР: Векторы  и
и  коллинеарны тогда и только тогда, когда точки, определяемые комплексными числами а—b и с—d, коллинеарны с началом О.
коллинеарны тогда и только тогда, когда точки, определяемые комплексными числами а—b и с—d, коллинеарны с началом О.
Замечание:
1. На основании (6) имеем:
 ; (8)
; (8)
2. Если точки А, В, С, D принадлежат единичной окружности  =l,то
=l,то
 , и поэтому условие (8) принимает вид:
, и поэтому условие (8) принимает вид:
 ; (9)
; (9)
3. Коллинеарность точек A , В, С характеризуется коллинеарностью векторов  и
и  . Используя (8), получаем:
. Используя (8), получаем:
 . (10)
. (10)
Это критерий принадлежности точек A , B , С одной прямой. Его можно представить в симметричном виде
 (11)
(11)
Если точки A и B принадлежат единичной окружности  =l, то
=l, то  , и поэтому каждое из соотношений (10) и (11) преобразуется (после сокращения на (а- b ) в такое:
, и поэтому каждое из соотношений (10) и (11) преобразуется (после сокращения на (а- b ) в такое:
 (12)
(12)
Точки А и В фиксируем, а точку С будем считать переменной, переобозначив ее координату через z. Тогда каждое из полученных соотношений (10), (11), (12) будет уравнением прямой АВ:
 , (10а)
, (10а)
 . (12a)
. (12a)
В частности, прямая ОА имеет уравнение 
Переходим к выводу критериев перпендикулярности отрезков. Ясно, что

Комплексные числа с аргументами  и
и  - являются чисто мнимыми.
- являются чисто мнимыми.
Поэтому,

или
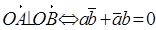 (13)
(13)
Отрезки АВ и CD перпендикулярны тогда и только тогда, когда векторы точек с комплексными координатами а— b и с— d перпендикулярны. В силу (13) имеем:
 (14)
(14)
В частности, когда точки А, В, С, D принадлежат единичной окружности  =l, то зависимость (14) упрощается:
=l, то зависимость (14) упрощается:
 (15)
(15)
Выведем уравнение касательной к единичной окружности  =l в ее точке
=l в ее точке
P (р). Если М (z) — произвольная точка этой касательной, то  и обратно. На основании (14) имеем:
и обратно. На основании (14) имеем:

или
 .
.
Поскольку  , то уравнение касательной становится таким:
, то уравнение касательной становится таким:
 . (16)
. (16)
Это частный случай уравнения (12a) при а= b =р. Решим еще две вспомогательные задачи, необходимые для решения содержательных геометрических задач.
Задача 1. Найти координату точки пересечения секущих АВ и CD единичной окружности  =l, если точки А, В, С, D лежат на этой окружности и имеют соответственно комплексные координаты а, b , с, d .
=l, если точки А, В, С, D лежат на этой окружности и имеют соответственно комплексные координаты а, b , с, d .
Пользуясь уравнением (12а), получаем систему

из которой почленным вычитанием находим:
 (17)
(17)
В том частном случае, когда хорды АВ и CD перпендикулярны, в силу (15) ab =- cd , и поэтому результат (17) приводится к виду

откуда
 (18)
(18)
В этом случае точка пересечения определяется только тремя точками A, В, С, так как  , и, значит,
, и, значит,
 (19)
(19)
3адача 2. Найти комплексную координату точки пересечения касательных в точках A (а) и B(b) единичной окружности  =l. Для искомой координаты z имеем систему
=l. Для искомой координаты z имеем систему

из которой находим:

Поскольку 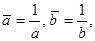 то получаем окончательно:
то получаем окончательно:
 или
или  (20)
(20)
Покажем теперь метод комплексных чисел в действии, применяя его к доказательству классических теорем элементарной геометрии.
Теорема Ньютона . В описанном около окружности четырехугольнике середины диагоналей коллинеарны, с центром окружности.

Доказательство. Примем центр окружности за начало, полагая ее радиус равным единице. Обозначим точки касания сторон данного четырехугольника AoBoCoDo через А, В, С, D (в круговом порядке) (рис.4). Пусть М и N — середины диагоналей АoСo и BoDo соответственно. Тогда согласно (20) точки Аo, Вo, Сo, Do будут иметь соответственно комплексные координаты:

где a, b, c, d – комплексные координаты точек A, B, C, D.
Поэтому

Вычисляем  Поскольку
Поскольку 
 то непосредственно видно, что
то непосредственно видно, что  На основании (6) точки О, М, N коллинеарны.
На основании (6) точки О, М, N коллинеарны.
Теорема Гаусса. Если прямая пересекает прямые, содержащие стороны ВС, СА, АВ треугольника АВС соответственно в точках А1, B1, C1, то середины отрезков АА1, ВВ1, СС1 коллинеарны (рис.5).
Доказательство. Используя (11), запишем условия коллинеарности троек точек АВ1С, СА1В, ВС1А, A1B1C1:
 (21)
(21)
Если М, N , P — середины отрезков AA 1 , BB 1 , CC 1 , то предстоит показать, что
 (22)
(22)
Так как  то доказываемое равенство (22) эквивалентно такому:
то доказываемое равенство (22) эквивалентно такому:

или после перемножения:
 (23)
(23)
Теперь легко видеть то, что (23) получается почленным сложением равенств (21). Доказательство закончено.
Теорема Паскаля . Точки пересечения прямых, содержащих противоположные стороны вписанного шестиугольника, лежат на одной прямой.
Доказательство. Пусть в окружность вписан шестиугольник ABCDEF и  (рис.6). Примем центр окружности за нулевую точку плоскости, а ее радиус - за единицу длины. Тогда согласно (17) имеем:
(рис.6). Примем центр окружности за нулевую точку плоскости, а ее радиус - за единицу длины. Тогда согласно (17) имеем:

Вычисляем

и аналогично

Далее находим:

|
|
Поскольку числа 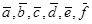 равны соответственно
равны соответственно  , то устная проверка обнаруживает, что найденное выражение совпадает со своим сопряженным, т. е. является действительным числом. Это означает коллинеарность точек М, N , Р.
, то устная проверка обнаруживает, что найденное выражение совпадает со своим сопряженным, т. е. является действительным числом. Это означает коллинеарность точек М, N , Р.
Teopeмa Mонжа . Во вписанном в окружность четырехугольнике прямые, проходящие через середины сторон и. каждой диагонали перпендикулярно противоположным сторонам и соответственно другой диагонали, пересекаются в одной точке. Она называется точкой Монжа вписанного четырехугольника.
Доказательство. Серединные перпендикуляры к сторонам четырёхугольника ABCD пересекаются в центре описанной окружности, который примем за начальную точку. Для каждой точки М( z ) серединного перпендикуляра к [AB] число  чисто мнимое.
чисто мнимое.
В частности, при z=0 оно равно  . Для каждой точки N ( z ) прямой, проходящей через середину стороны CD перпендикулярно (AB), число
. Для каждой точки N ( z ) прямой, проходящей через середину стороны CD перпендикулярно (AB), число  необходимо будет чисто мнимым и обратно. Но для z=
необходимо будет чисто мнимым и обратно. Но для z=  оно равно
оно равно 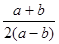 т. е. чисто мнимое. Следовательно, точка Е с комплексной координатой
т. е. чисто мнимое. Следовательно, точка Е с комплексной координатой
 лежит на указанной прямой. А это выражение симметрично относительно букв а, b, с, d. Поэтому и остальные пять аналогично построенных прямых содержат точку Е.
лежит на указанной прямой. А это выражение симметрично относительно букв а, b, с, d. Поэтому и остальные пять аналогично построенных прямых содержат точку Е.
Решим ещё несколько основных планиметрических задач.
3адача 3. Доказать, что диагонали четырехугольника ABCD, вписанного в окружность, перпендикулярны тогда и только тогда, когда сумма квадратов двух его противоположных сторон равна сумме квадратов двух других противоположных сторон.
Решение. Требуется доказать: 
Запишем 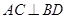 используя (15):
используя (15):  . Тогда, воспользовавшись формулами (15), (2) и тем, что точки A , B , C , D принадлежат окружности
. Тогда, воспользовавшись формулами (15), (2) и тем, что точки A , B , C , D принадлежат окружности  , приходим к выводу, что
, приходим к выводу, что 
3адача 4. Доказать, что если средние линии MP , NQ четырехугольника ABCD равны, то его диагонали AC и BD перпендикулярны и обратно.
Решение. Требуется доказать:  .
.
(a)  так как
так как
 , cогласно (4a). Подставим эти выражения в равенства (a) и получим:
, cогласно (4a). Подставим эти выражения в равенства (a) и получим:  но это и есть условие того, что
но это и есть условие того, что  (см. 14).
(см. 14).
|
из
5.00
|
Обсуждение в статье: Геометрическая интерпретация комплексных чисел. Длина отрезка |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы



