 |
Главная |
Углы и площади. Критерий принадлежности четырех точек одной окружности
|
из
5.00
|
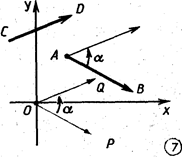
Условимся обозначать символом 
 положительно ориентированный угол, на который надо повернуть вектор
положительно ориентированный угол, на который надо повернуть вектор  , чтобы он стал сонаправлен
, чтобы он стал сонаправлен
с вектором 
 . Если
. Если 
 и
и  , то точкам Р и Q соответствуют комплексные числа b—а и d—c(рис.7) и
, то точкам Р и Q соответствуют комплексные числа b—а и d—c(рис.7) и
 (24)
(24)
Эта формула в применении к положительно ориентированному треугольнику АВС дает:
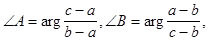
 (25)
(25)
Если z=r( 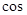
 ,то
,то  Отсюда
Отсюда
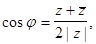


 (26)
(26)
Тогда 
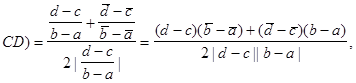

 так как
так как 
Итак,
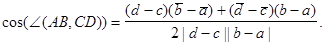 (27)
(27)
Аналогично находим:
 . (28)
. (28)
Выведем формулу для площади S положительно ориентированного треугольника АВС:




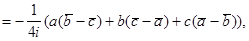
или
 (29)
(29)
что можно записать в виде определителя третьего порядка:
 (30)
(30)
Если треугольник АВС вписан в окружность  , то формула (29) преобразуется к виду
, то формула (29) преобразуется к виду
 . (31)
. (31)
Для площади S положительно ориентированного четырехугольника ABCD имеем:
 (32)
(32)
Если четырехугольник ABCD вписан в окружность zz==l, то (32) принимает вид:
 (33)
(33)
Три произвольно взятые точки всегда принадлежат либо одной окружности, либо одной прямой. Критерии принадлежности трех точек одной прямой рассмотрены выше.
Докажем КРИТЕРИЙ принадлежности четырех точек одной окружности или прямой.
Возьмем четыре произвольные точки A , В, С, D соответственно с комплексными координатами а, b,c,d. Комплексное число
 (34)
(34)
называется двойным отношением точек A, В, С, D и обозначается (AB, CD). Порядок точек существен.
Теорема. Для того чтобы, четыре точки лежали на одной прямой или на одной окружности, необходимо и достаточно, чтобы их двойное отношение было действительным числом.
Доказательство. Если точки А, В, С, D коллинеарны, то отношения  и
и 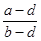 действительные числа (см. условие (10)). Следовательно, в этом случае будет действительным и двойное отношение (34). Если точки А, В, С, D лежат на окружности, то рассмотрим два возможных случая:
действительные числа (см. условие (10)). Следовательно, в этом случае будет действительным и двойное отношение (34). Если точки А, В, С, D лежат на окружности, то рассмотрим два возможных случая:
1) точки С и D находятся в одной полуплоскости от прямой АВ;
2) точки С и D находятся в различных полуплоскостях от прямой АВ.
В первом случае ориентированные углы ВСА и BDA равны, во втором случае  ВСА+
ВСА+  АDВ= ±
АDВ= ±  , т. е.
, т. е.  ВСА-
ВСА-  ВСА= ±
ВСА= ±  . В обоих случаях разность
. В обоих случаях разность  равна нулю или ±
равна нулю или ±  . Но поскольку согласно (24) эта разность равна
. Но поскольку согласно (24) эта разность равна

то 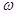 — действительное число.
— действительное число.
Обратно: если двойное отношение четырех точек действительно, то эти точки или коллинеарны, или принадлежат одной окружности. В самом деле, тогда если  действительное число, то и
действительное число, то и 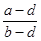 действительное число. Поэтому точки А, В, С коллинеарны и точки А, В, D коллинеарны, и, значит, все четыре точки коллинеарны. Если же число
действительное число. Поэтому точки А, В, С коллинеарны и точки А, В, D коллинеарны, и, значит, все четыре точки коллинеарны. Если же число 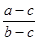 комплексное, то и число
комплексное, то и число 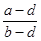


 также комплексное, отличное от действительного. Поэтому точки A, B, С неколлинеарны и точки А, В, D также неколлинеарны. Так как по условию двойное отношение вещественно, то
также комплексное, отличное от действительного. Поэтому точки A, B, С неколлинеарны и точки А, В, D также неколлинеарны. Так как по условию двойное отношение вещественно, то
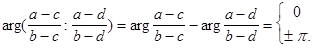
Следовательно, либо  BCA =
BCA =  BDA , либо
BDA , либо  ВСА—
ВСА—  В D А=±
В D А=±  , т.е.
, т.е. 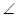 ВСА+
ВСА+ 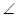 ADB =±
ADB =±  . В первом случае отрезок АВ из точек С и D виден под равными углами, и, стало быть, они принадлежат одной дуге окружности, стягиваемой хордой АВ. Во втором случае сумма противоположных углов четырехугольника ACBD равна ±
. В первом случае отрезок АВ из точек С и D виден под равными углами, и, стало быть, они принадлежат одной дуге окружности, стягиваемой хордой АВ. Во втором случае сумма противоположных углов четырехугольника ACBD равна ±  , и поэтому он будет вписанным в окружность. Доказательство закончено.
, и поэтому он будет вписанным в окружность. Доказательство закончено.
Задача 1. В окружности проведены три параллельные хорды  Доказать, что для произвольной точки М окружности прямые
Доказать, что для произвольной точки М окружности прямые  образуют равные углы соответственно с прямыми ВС, СА, АВ.
образуют равные углы соответственно с прямыми ВС, СА, АВ.
Решение. Принимая окружность за единичную, отнесем точкам А, В, С, A 1 , B 1 , C 1 комплексные числа  Тогда по условию (9) параллельности хорд имеем
Тогда по условию (9) параллельности хорд имеем 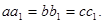 Следует доказать, что
Следует доказать, что  (рис.8).
(рис.8).
Первое равенство эквивалентно такому: 
Или

т. е. эта дробь должна быть числом действительным. А это имеет место, поскольку сопряженное ей число

равно этой же дроби. Аналогично доказывается и второе равенство углов.
Задача 2. На плоскости даны четыре окружности  так, что окружности
так, что окружности  и
и 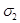 пересекаются в точках
пересекаются в точках  и
и  ; окружности
; окружности 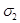 и
и  пересекаются в точках
пересекаются в точках  и
и 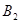 , окружности
, окружности  и
и  — в точках
— в точках  и
и  и окружности
и окружности  и
и  — в точках
— в точках  и
и  . Доказать, что если точки
. Доказать, что если точки 
 лежат на одной окружности или прямой, то и точки
лежат на одной окружности или прямой, то и точки  также лежат на одной
также лежат на одной

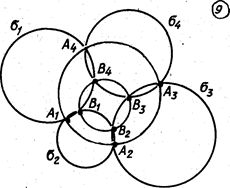
окружности или прямой (рис.9).
Решение. Согласно теореме этого параграфа и условию задачи будут действительрыми двойные отношения:

Поэтому будет действительным и число

Следовательно, из вещественности двойного отношения  вытекает вещественность и двойного отношения
вытекает вещественность и двойного отношения  .
.
Подобные и равные треугольники. Правильный треугольник
ОПР: Треугольники АВС и 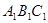 подобны и одинаково ориентированы (подобие первого рода), если только
подобны и одинаково ориентированы (подобие первого рода), если только  и
и 
(углы ориентированные).
Эти равенства с помощью комплексных чисел можно записать так:
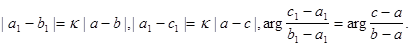
Два равенства  и
и  эквивалентны одному
эквивалентны одному  или
или
 (35)
(35)
где  комплексное число,
комплексное число,  коэффициент подобия.
коэффициент подобия.
Если, в частности,  - число действительное, то
- число действительное, то  и на основании признака (8) будет
и на основании признака (8) будет  . По такой же причине
. По такой же причине  и
и  . Следовательно, треугольники
. Следовательно, треугольники  и
и  гомотетичны.
гомотетичны.
Соотношение (35) — необходимый н достаточный признак того, что треугольники АВС и  являются подобными и одинаково ориентированными. Ему можно придать симметричный вид:
являются подобными и одинаково ориентированными. Ему можно придать симметричный вид:
 (36)
(36)
или
 . (37)
. (37)
ОПР. Треугольники АВС и  подобны и противоположно ориентированы (подобие второго рода),
подобны и противоположно ориентированы (подобие второго рода), 
 и
и  . Последнее равенство дает:
. Последнее равенство дает:

Два равенства
 и
и 
эквивалентны одному

или
 (38)
(38)
где  - комплексное число,
- комплексное число,  -коэффициент подобия.
-коэффициент подобия.
Соотношение (38) есть необходимый и достаточный признак того, что треугольники АВС и  подобны и ориентированы противоположно. Его можно записать в симметричной форме:
подобны и ориентированы противоположно. Его можно записать в симметричной форме:
 (39)
(39)
или же так:
 (40)
(40)
Если  , то треугольники АВС и
, то треугольники АВС и  будут равны (конгруэнтны).
будут равны (конгруэнтны).
Тогда соотношения (35) и (38) становятся признаками равенства треугольников соответственно одинаковой и противоположной ориентации.
Рассмотренные признаки подобия треугольников позволяют обосновать простой способ построение произведения и частного двух комплексных чисел. Пусть даны точки  с комплексными координатами
с комплексными координатами  и требуется построить точку М с координатой z = ab . Тогда, очевидно,
и требуется построить точку М с координатой z = ab . Тогда, очевидно,  . Это равенство говорит о том, что треугольники ОЕА и ОВМ подобны и одинаково ориентированы. Отсюда и вытекает способ построения точки М, соответствующей произведению ab (рис.10).
. Это равенство говорит о том, что треугольники ОЕА и ОВМ подобны и одинаково ориентированы. Отсюда и вытекает способ построения точки М, соответствующей произведению ab (рис.10).
Обратно: если даны точки М и А соответственно с координатами ab и a, то точка В, соответствующая частному этих чисел строится на основании тех, же подобных треугольников.
Следует обратить внимание на один важный частный случай. Если |а|=1, то точка М будет образом точки В при повороте около нулевой точки на угол  . Если потребовать, чтобы ориентированный треугольник АВС был подобен ориентированному треугольнику BCA , то треугольник АВС необходимо будет правильным. Поэтому из условия (36) получаем необходимое и достаточное условие того, чтобы треугольник АВС был правильным
. Если потребовать, чтобы ориентированный треугольник АВС был подобен ориентированному треугольнику BCA , то треугольник АВС необходимо будет правильным. Поэтому из условия (36) получаем необходимое и достаточное условие того, чтобы треугольник АВС был правильным
 (41)
(41)
или
 (42)
(42)
Введем в употребление комплексное число  являющееся одним из корней уравнения
являющееся одним из корней уравнения  (Формула для нахождения корней -
(Формула для нахождения корней -  ) Другие два корня которого равны 1 и
) Другие два корня которого равны 1 и 
 . По теореме Виета для кубического уравнения
. По теореме Виета для кубического уравнения  имеем
имеем 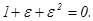 Это легко проверить и непосредственно. Тогда равенство (41) будет эквивалентно такому:
Это легко проверить и непосредственно. Тогда равенство (41) будет эквивалентно такому:



или после умножения первого трехчлена на 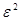 :
:
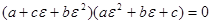 . (43)
. (43)
Итак, для того чтобы треугольник АВС был правильным, необходимо и достаточно выполнения хотя бы одного из равенств:
 (44)
(44)
или же
 (45)
(45)
Оказывается, первое из этих равенств соответствует только тому случаю, когда треугольник АВС ориентирован положительно, а второе выполняется лишь при отрицательной его ориентации. В самом деле, так как умножению на  отвечает поворот на
отвечает поворот на  , то при положительной ориентации треугольника
, то при положительной ориентации треугольника  (рис.11), откуда
(рис.11), откуда 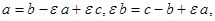 и поэтому
и поэтому 
Аналогично проверяется выполнение равенства (45) для отрицательно ориентированного правильного треугольника АВС. Очевидно, одновременно равенства (44) и (45) выполняться не могут.
Если правильный треугольник АВС вписан в окружность  , то при его положительной ориентации
, то при его положительной ориентации  и
и 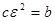 , а при отрицательной ориентации
, а при отрицательной ориентации  и
и  Поэтому каждое из условий (44) и (45) принимает вид:
Поэтому каждое из условий (44) и (45) принимает вид:
 (46)
(46)
Задача 1. Доказать, что треугольник  , стороны которого принадлежат касательным в вершинах треугольника АВС к его описанной окружности, гомотетичен треугольнику с вершинами в основаниях
, стороны которого принадлежат касательным в вершинах треугольника АВС к его описанной окружности, гомотетичен треугольнику с вершинами в основаниях 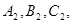 высот треугольника АВС.
высот треугольника АВС.
Решение. Принимаем описанную окружность за единичную 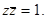 Руководствуясь формулами (20) и (19), получаем:
Руководствуясь формулами (20) и (19), получаем:

Проверяем выполнимость признака (35):

причем 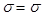 , т. е.
, т. е.  -действительное число. Значит, треугольники
-действительное число. Значит, треугольники  и
и  гомотетичны.
гомотетичны.
3адача 2. Два равных одинаково ориентированных треугольника АВС и  вписаны в одну окружность. Доказать, что треугольник с вершинами в точках пересечения прямых ВС и
вписаны в одну окружность. Доказать, что треугольник с вершинами в точках пересечения прямых ВС и  , СА и
, СА и  , AB и
, AB и  подобен данным треугольникам.
подобен данным треугольникам.
Решение. Придадим окружности уравнение  . Вершины. треугольника
. Вершины. треугольника  служат образами вершин треугольника АВС при повороте на некоторый угол
служат образами вершин треугольника АВС при повороте на некоторый угол 
 . Поэтому
. Поэтому  Если
Если  — точки пересечения прямых ВС и
— точки пересечения прямых ВС и  СА и
СА и  АВ и
АВ и  соответственно, то на основании (17)
соответственно, то на основании (17)  откуда
откуда 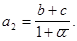 Аналогично
Аналогично 
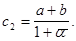
Осталось проверить условие (17):  что делается непосредственной подстановкой.
что делается непосредственной подстановкой.
3адача 3. Доказать, что середины отрезков, соединяющих соответственные вершины двух равных и противоположно ориентированных треугольников, коллинеарны.
Решение. Для доказательства данной задачи воспользуемся:
1) Формулой (38),- необходимое и достаточное условие равенства двух противоположно ориентированных треугольников ABC и 
 ;
;
2) Формулой (4а) для точек M , N , P: 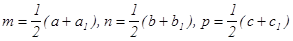 (из условия задачи);
(из условия задачи);
3) Формулой (11),- коллинеарности точек M , N , P: 
Теперь простой проверкой убеждаемся в том, что из 1)  2)
2)  3).
3).
ПРЯМАЯ И ОКРУЖНОСТЬ НА ПЛОСКОСТИ КОМПЛЕКСНЫХ ЧИСЕЛ
Пусть произвольной точке М плоскости комплексных чисел соответствует комплексное число  . Из равенств
. Из равенств  и
и  однозначно выражаются декартовы координаты х и у точки М через комплексные числа
однозначно выражаются декартовы координаты х и у точки М через комплексные числа 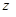 и
и  :
:
 (1)
(1)
Поэтому комплексные числа z и  называются сопряженными комплексными координатами этой точки.
называются сопряженными комплексными координатами этой точки.
Формулы (1) позволяют осуществить переход от уравнения геометрической фигуры в декартовых координатах к ее уравнению в сопряженных комплексных координатах. Однако сейчас мы предпочли непосредственное рассмотрение уравнений в сопряженных комплексных координатах.
Геометрический смысл уравнения 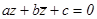
Найдем множество точек плоскости, сопряженные комплексные координаты которых удовлетворяют уравнению
 (2)
(2)
Сначала выделим особый случай, когда с=0. Тогда имеем систему относительно  и
и 

второе уравнение которой получается из первого переходом к сопряженным числам. Уравнивая коэффициенты при  , путем вычитания второго уравнения из первого получаем:
, путем вычитания второго уравнения из первого получаем:

Если  , т.е.
, т.е.  , то решением полученного уравнения, а значит, и решением исходного уравнения
, то решением полученного уравнения, а значит, и решением исходного уравнения  будет единственное число z=0. При
будет единственное число z=0. При  уравнение
уравнение  напишем в виде
напишем в виде  . Модули левой и правой частей равны. Необходимо, чтобы
. Модули левой и правой частей равны. Необходимо, чтобы  , откуда
, откуда  . Этому условию удовлетворяет каждая точка прямей m, проходящей через начало под углом
. Этому условию удовлетворяет каждая точка прямей m, проходящей через начало под углом  к действительной оси (рис.1). Так, уравнением
к действительной оси (рис.1). Так, уравнением
 (3)
(3)
| |
задается прямая при 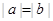 и точка
и точка  при
при  .
.
Пусть теперь  . Свободный член уравнения (2) можно всегда сделать действительным числом путем умножения обеих частей уравнения на с. Поэтому сразу будем полагать
. Свободный член уравнения (2) можно всегда сделать действительным числом путем умножения обеих частей уравнения на с. Поэтому сразу будем полагать  Тогда имеем систему:
Тогда имеем систему:

из которой получаем:  . Рассмотрим возможные случаи.
. Рассмотрим возможные случаи.
Если  , то
, то  и подстановкой в исходное уравнение получаем:
и подстановкой в исходное уравнение получаем:  или
или  .
.
При  его решение единственно:
его решение единственно:

При  решений нет.
решений нет.
Если  , то
, то  и
и  , т. е.
, т. е.  . В этом случае уравнением (2) при
. В этом случае уравнением (2) при  прямая. В самом деле, возьмем точку
прямая. В самом деле, возьмем точку  и вектор
и вектор  точки В( b ) и рассмотрим множество точек М(z), для каждой из которых ( MQ )
точки В( b ) и рассмотрим множество точек М(z), для каждой из которых ( MQ )  ( OB ):
( OB ):
 (4)
(4)
Очевидно, это множество есть прямая. При 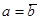 и
и  уравнение (4) эквивалентно уравнению (2).
уравнение (4) эквивалентно уравнению (2).
Таким образом, при  и
и  уравнение (2) есть уравнение прямой, которая проходит через точку
уравнение (2) есть уравнение прямой, которая проходит через точку 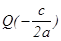 перпендикулярно вектору
перпендикулярно вектору  .
.
Наконец, отметим случай, когда 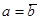 , но
, но  . Тогда система
. Тогда система

приводит к противоречию:  , т.е.
, т.е.  .
.
Подведем итоги. Уравнением  , в котором хотя бы один из коэффициентов a и b отличен от нуля, задается:
, в котором хотя бы один из коэффициентов a и b отличен от нуля, задается:
1) прямая при |а|=| b |, с=0, а также при  ;
;
2) единственная точка при  ;
;
3) пустое множество в иных случаях, т. е. при | a | = | b |,  , а также при
, а также при 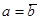 ,
,  .
.
Достигнув поставленной цели, возвратимся снова к системе:

не налагая ограничений на коэффициенты а, b , с, кроме того, что a и b не равны нулю одновременно. Уравнивая коэффициенты при  , приходим к уравнению
, приходим к уравнению  , которое:
, которое:
а) имеет единственное решение при  ;
;
б) имеет бесконечное множество решений при  и
и  ;
;
в) не имеет решений при  и
и  .
.
Отсюда и на основании результата предыдущих исследований получаем, что уравнение 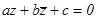 определяет:
определяет:
а) единственную точку при 
б) прямую при  и
и  ;
;
в) пустое множество при  и
и  .
.
Уравнение
 (5)
(5)
прямой в сопряженных комплексных координатах будем называть приведенным уравнением прямой.
Две прямые. Расстояние от точки до прямой
Пусть прямая т задана приведенным уравнением  . Так как она перпендикулярна вектору
. Так как она перпендикулярна вектору  , то вектор
, то вектор  будет ей параллелен (рис.2). Следовательно, ориентированный угол от оси х до прямой т равен аргументу числа ai :
будет ей параллелен (рис.2). Следовательно, ориентированный угол от оси х до прямой т равен аргументу числа ai :
|
|
 . (6)
. (6)
Положительно ориентированный угол  от прямой
от прямой  до прямой
до прямой  равен углу между их направляющими векторами
равен углу между их направляющими векторами  и
и  :
:
 . (7)
. (7)
Формулы (6) и (7) позволяют находить соответствующие углы с точностью до слагаемого  .
.
Из формулы (7) вытекает критерий перпендикулярности и критерий параллельности прямых  и
и  . В самом деле,
. В самом деле,  чисто мнимое число. Это значит, что
чисто мнимое число. Это значит, что  , или
, или
 . (8)
. (8)
При  или
или  получаем:
получаем:
 . (9)
. (9)
Если прямая  проходит через точку
проходит через точку  , то
, то  и ее уравнение можно написать в виде:
и ее уравнение можно написать в виде:
 (10)
(10)
В силу условия (8) перпендикулярности для прямой, перпендикулярной данной, коэффициентами при, z и 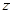 будут соответственно числа а и
будут соответственно числа а и  . Поэтому на основании уравнения (10) получаем уравнение
. Поэтому на основании уравнения (10) получаем уравнение
 (11)
(11)
прямой, проходящей через точку  перпендикулярно прямой
перпендикулярно прямой  . Решение системы
. Решение системы

дает координату
 (12)
(12)
основания M 1 перпендикуляра, опущенного из точки  на прямую
на прямую  .
.
Так как расстояние d от точки M0 этой прямой равно  , то
, то
 . (13)
. (13)
Геометрический смысл, уравнения 
Из формулы расстояния между двумя точками получается уравнение окружности по ее центру S ( s ) и радиусу R :
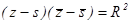 (14)
(14)
Пусть дано уравнение
 , (15)
, (15)
в котором на комплексные коэффициенты а, b , с не накладывается заранее никаких условий. Требуется найти множество точек, координаты которых ему удовлетворяют. С этой целью удобно представить его в эквивалентном виде:
 . (16)
. (16)
Рассмотрим все возможные случаи для коэффициентов а, b , с.
1. Сравнивая уравнение (16) с уравнением (14) окружности, приходим к выводу, что уравнение (16), а значит, и уравнение (15) задают окружность тогда и только тогда, когда




