 |
Главная |
Метод Нелдера-Мида (деформируемого многогранника)
|
из
5.00
|
Метод Ньютона-Рафсона
Алгоритм метода:

здесь:
·  - направление спуска
- направление спуска
·  - шаг выбирается из условия убывания функции в точках последовательности:
- шаг выбирается из условия убывания функции в точках последовательности:
 .
.
Геометрическая интерпретация метода для квадратичной функции:
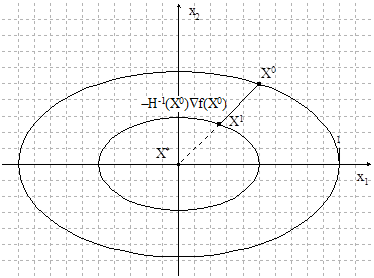
Рисунок 1.10. Геометрическая интерпретация метода
Основной критерий окончания метода: 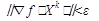
Начальные параметры метода: 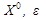 .
.
Изменяемый параметр метода: величина шага 
1.1.9 Метод Марквардта
Метод Марквардта (метод Ньютона с переменной матрицей), повторяет метод Ньютона. Отличие заключается в том, что точки строятся по закону:
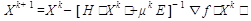
где  - последовательность чисел (>0), обеспечивающих положительную определенность матрицы
- последовательность чисел (>0), обеспечивающих положительную определенность матрицы  . Обычно
. Обычно  назначается как минимум на порядок больше, чем самый большой элемент матрицы
назначается как минимум на порядок больше, чем самый большой элемент матрицы  .
.
Метод Нелдера-Мида (деформируемого многогранника)
Алгоритм метода:
1) Задается начальная система точек (многогранник), включающая в себя  точку:
точку:

для функции 2-х переменных задается три начальные точки:

2) Вычисляется значение функции во всех точках многогранника и выбирается:
лучшая точка  :
:  (здесь
(здесь  - номер итерации,
- номер итерации,  - номер точки) худшая точка
- номер точки) худшая точка  :
: 
Далее заданная система из  точки перестраивается, для этого:
точки перестраивается, для этого:
3) Строится центр тяжести системы заданных точек за исключением худшей:

(для функции 2-х переменных точка  - середина отрезка, соединяющего точки за исключением худшей)
- середина отрезка, соединяющего точки за исключением худшей)
4) Выполняется операция отражение худшей точки через центр тяжести:

здесь  - параметр отражения (рекомендуемое значение
- параметр отражения (рекомендуемое значение 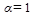 ).
).
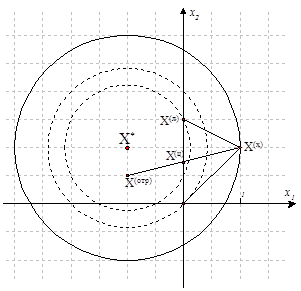
Рисунок 1.11. Отражение
5) Формируется новая система точек (многогранник). Для этого в точке  вычисляется значение функции, полученное значение сравнивается с
вычисляется значение функции, полученное значение сравнивается с  :
:
если  выполняется операция растяжение:
выполняется операция растяжение:


Рисунок 1.12. Растяжение
здесь 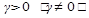 - параметр растяжения (рекомендованное значение
- параметр растяжения (рекомендованное значение  )
)
При этом если  , то в новой системе точек точка
, то в новой системе точек точка  будет заменена на
будет заменена на  , если же
, если же  , то в новой системе точек точка
, то в новой системе точек точка  будет заменена на
будет заменена на 
l если  выполняется операция сжатие:
выполняется операция сжатие:


Рисунок 1.13. Сжатие
здесь  - параметр сжатия (рекомендованное значение
- параметр сжатия (рекомендованное значение  ).
).
При этом если  , то в новой системе точек точка
, то в новой системе точек точка  будет заменена на
будет заменена на  , если же
, если же  , то в новой системе точек точка
, то в новой системе точек точка  будет заменена на
будет заменена на  .
.
l если  выполняется операция редукции: при этом формируется новый многогранник, содержащий точку
выполняется операция редукции: при этом формируется новый многогранник, содержащий точку  с уменьшенными вдвое сторонами:
с уменьшенными вдвое сторонами:


Рисунок 1.14. Редукция
Т.о. в результате выполнения этого пункта алгоритма формируется новая система точек (многогранник), причем в случае возникновения операций растяжения и сжатия перестраивается только одна точка -  , в случае возникновения операции редукции – все точки, за исключением
, в случае возникновения операции редукции – все точки, за исключением 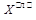 .
.
6) Процедура 2)-5) повторяется до выполнения критерия окончания счета.
Основной критерий окончания метода:

Дополнительные критерии окончания метода:
l при выполнении предельного числа итераций:

при однократном или двукратном одновременном выполнении двух условий:
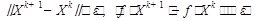 ,
,
где  - малое положительное число.
- малое положительное число.
Алгоритм работы метода Нелдера-Мида схематически изображен на рис. 1.15

Рисунок 1.15. Диаграмма работы метода Нелдера-Мида
|
из
5.00
|
Обсуждение в статье: Метод Нелдера-Мида (деформируемого многогранника) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

