Основные сведения из математического программирования

Раздел 2 . Экономико-математические методы и прикладные модели

Для анализа и прогнозирования экономических процессов наряду с традиционными экономическими методами (например, индексный, сравнительный), и аналитическими показателями (например, темпы прироста, коэффициенты эластичности) используются и экономико-математические методы и модели. Обычно экономико-математические модели (ЭММ) разрабатываются в тех случаях, когда решить экономические проблемы в условиях традиционных методов обработки информации не представляется возможным. Основная цель разработки прикладной ЭММ заключается в создании инструмента комплексного анализа и прогноза и на этой основе расширение информационной базы принятия управляющих решений и усиления степени обоснованности принимаемых решений.

Глава 8. Математическое программирование и оптимизационные модели

Задачи линейного программирования были первыми подробно изученными задачами математического программирования. В 1820 г. Ж. Фурье и затем в 1947г. Дж. Данциг предложил метод направленного перебора смежных вершин в направлении возрастания целевой функции — симплекс-метод, ставший основным при решении задач линейного программирования.

Присутствие в названии термина «программирование» объясняется тем, что первые исследования и первые приложения линейных оптимизационных задач были в сфере экономики, так как в английском языке слово «programming» означает планирование, составление планов или программ. Поэтому наименование «Математическое программирование» связано с тем, что целью решения задач является выбор оптимальной программы действий.

Одним из первых, исследовавшим в общей форме задачи линейного программирования, был советский академик, лауреат Нобелевской премии (1975 г.) Л.В.Канторович, сформулировавший ряд задач линейного программирования в сфере экономики и предложивший (1939 г.) метод их решения (метод разрешающих множителей ), незначительно отличающийся от симплекс-метода.

Л. В. Канторовичем совместно с М. К. Гавуриным в 1949 г разработан метод потенциалов, который применяется при решении транспортных задач. В последующих работах Л. В. Канторовича, В. С. Немчинова, В. В. Новожилова, А. Л. Лурье, А. Брудно, А. Г. Аганбегяна, Д. Б. Юдина, Е. Г. Гольштейна и других математиков и экономистов получили дальнейшее развитие как математическая теория линейного и нелинейного программирования, так и приложение её методов к исследованию различных экономических проблем.

Задачи математического программирования применительно к различным экономическим объектам формулируются в виде конкретных оптимизационных моделей. Оптимизационные (экстремальные) модели в экономике возникают при практической реализации принципа оптимальности в управлении, например, при управлении  ограниченными ресурсами в логистических системах. Такими системами, в первую очередь, являются предприятия отраслей материального производства, транспортные компании, современные системы складирования и др. Цель оптимизационных моделей состоит в нахождении наилучшего (с точки зрения заданного критерия) распределения ресурсов. Например, определение оптимальной производственной программы предприятия с позиций, например, максимальной прибыли, которая достигается при наилучшем распределении ресурсов в рамках заданных ограничений; определение оптимальных схем перевозок с позиций достижения минимума транспортной работы по доставке груза в рамках заданных производственных мощностей производителей, складских площадей и потребностей потребителей; оптимальные варианты раскроя материала, обеспечивающие минимум отходов при удовлетворении потребностей в заготовках требуемого размера и др. В данном пособии описаны лишь базовые оптимизационные модели. С расширенными модификациями базовых моделей можно ознакомиться в [2-7].

Современные возможности ПЭВМ и мощное программное обеспечение устраняют технические проблемы компьютерной реализации оптимизационных моделей и в части формирования информационной базы модели, и в части компьютерного решения модели. Следует отметить, что зарубежные корпоративные информационные системы (КИС), которые по своей сути являются системами управления, включают данный класс моделей. В отличие от зарубежных, отечественные информационные системы (1С, Галактика), являясь информационно-аналитическими,  пока не выполняют функции управления, и встраивание в их структуру оптимизационных моделей рассматривается нами как перспективная задача, связанная с дальнейшим развитием этих систем.

Основные сведения из математического программирования

Математическое программирование — это область математики, в которой рассматривается теория и численные методы решения задач на экстремум функции многих переменных, когда на эти переменные наложены дополнительные ограничения, играющие существенную роль при решении задачи.

Модель задачи математического программирования включает: совокупность неизвестных величин х₁, х₂, …, х _n; целевую функцию (показатель эффективности, критерий оптимальности, функцию цели и др.); условия (или систему ограничений), налагаемые на неизвестные величины, совокупность которых образует область допустимых решений (Ω). Таким образом, мы можем записать математическую модель в следующем виде

F = f(х₁, х₂, …, х _n )→ max ( min )

( i = )                                                (8.1)

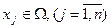
Линейное программирование — это частный раздел математического программирования, когда все функции  и  модели (8.1) линейны относительно переменных.

Общую постановку задачи линейного программирования можно записать в более компактной форме:

найти максимум или минимум функции.

f ( )= f (х₁, х₂, …, х _n )=                                        (8.2)

при ограничениях

                                            (8.3)

                                                                (8.4)

Вектор =(х₁, х₂, …,х _n ) (набор управляющих переменных) называется допустимым решением, или планом задачи, или вектором управления, или поведением оптимального программирования, если он удовлетворяет системе ограничений (8.3) и (8.4). Неотрицательное базисное допустимое решение задачи называется опорным планом. А тот план =(х₁, х₂, …,х _n ) (опорное решение), который доставляет максимум или минимум целевой функции f (х₁, х₂, …, х _n ) (8.2), называется оптимальным планом (оптимальным поведением, или просто решением) задачи линейного программирования.

Наиболее распространенным методом решения задач линейного программирования является так называемый симплексный метод – метод последовательного улучшения планов.

Суть этого метода заключается в том, что вначале получают допустимый план, удовлетворяющий всем ограничениям, но необязательно оптимальный (так называемое начальное опорное решение), оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций). Итак симплекс-метод распадается на два этапа:

1. находится любой опорный план задачи;

2. отправляясь от найденного плана, последовательно улучшают его и находят оптимальный.

Если найти значение целевой функции во всех крайних точках многогранника планов (а их не более ) и сравнить их, выбирая наилучшее, то данный процесс сравним по трудности с решением исходной задачи. Поэтому, согласно основной теоремы линейного программирования лучше рационально перебирать эти крайние точки.

Теорема 8.1. (основная теорема линейного программирования) Если ЗЛП имеет решение, то целевая функция достигает экстремального значения хотя бы в одной из крайних точек многогранника решений. Если же целевая функция достигает экстремального значения более чем в одной точке, то она достигает того же значения в любой точке, являющейся их выпуклой линейной комбинацией.

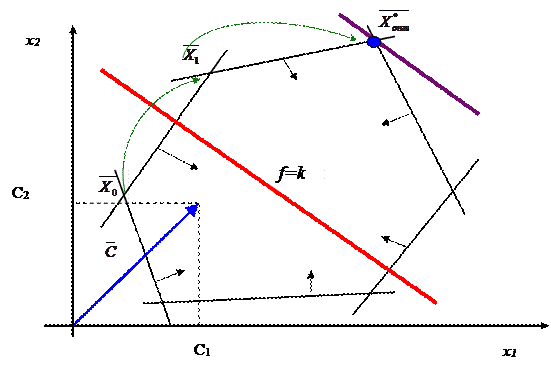Суть симплекс-метода: если известна какая-нибудь крайняя точка ( )

 

Рисунок 8.1. Геометрическая интерпретация решения симплексным методом

 

(смотри рисунок 8.1) и значение функции в ней, то все крайние точки, в которых значение функции хуже (предположим решается задача на максимум), нас не интересуют. Отсюда стремление найти способ перехода от данной точки к смежной по ребру ( ) и лучшей, и т.д. пока не придем в точку , где функция принимает оптимальное значение в данной области допустимых решений. Однако надо еще найти признак того, что лучших точек, чем эта, вообще нет.

Нахождение начального опорного решения и переход к следующему опорному решению проводятся на основе применения метода Жордана-Гаусса для системы линейных уравнений в канонической форме, в которой должна быть предварительно записана исходная задача. Результат каждой итерации (включая данные задачи) удобно записывать в виде симплексной таблицы (вид которой представлен ниже). Направление перехода от одного опорного решения к другому выбирается при этом на основе критерия оптимальности (целевой функции) исходной задачи. Симплекс-метод основан на следующих свойствах ЗЛП:

1.   Множество всех планов задачи линейного программирования выпукло.

2.   Не существует локального экстремума, отличного от глобального. Другими словами, если целевая функция принимает экстремальное значение, то данное значение будет единственным.

3.   Целевая функция задачи линейного программирования достигает своего максимального (минимального) значения в крайней точке многогранника решений (в его вершине). Если целевая функция принимает свое оптимальное значение более чем в одной крайней точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.

4.   Каждой угловой точке многогранника решений отвечает опорный план задача линейной оптимизации.

Предположим, что в симплексной таблице содержится некоторый опорный план. Через конечное число шагов либо будет найден оптимальный план задачи, либо будет установлено неразрешимость задачи. Перебор опорных планов осуществляется в процессе перехода от одного базиса системы переменных к другому базису. При этом приходится определять переменные, участвующие в преобразовании базиса. Переменная, включаемая в базис в задаче максимизации определяется по отрицательному коэффициенту в строке целевой функции симплексной таблицы. Если таких коэффициентов несколько, то выбирают максимальный по модулю. Такую переменную называют разрешающей, а столбец коэффициентов при ней разрешающим. Для выбора переменной исключаемой из базиса составляют симплексные отношения: это отношение свободного коэффициента к элементу такого же знака разрешающего столбца. Наименьшее из них и указывает уравнение (разрешающее), в котором содержится исключаемая переменная. После выбора разрешающего столбца и разрешающей строки определяется на их пересечении разрешающий элемент и осуществляется преобразование модели задачи к новому базису по правилам симплексных преобразований.

С каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной. Целевая функция и ограничения, наложенные на переменные двойственной задачи определяются условием исходной задачи. Первая и двойственная задачи образуют пару взаимно двойственных задач.

Для ЗЛП общего вида:

(I)	(II)    (8.5)

Согласно теории линейного программирования каждой оптимизационной задаче линейного программирования соответствует двойственная ей задача. Основные утверждения о взаимодвойственных задачах содержатся в следующих теоремах, называемых теоремами двойственности.

Теорема 8.2. Для любых допустимых планов  и  прямой и двойственной ЗЛП справедливо неравенство , т.е.

                                                                               (8.6)

Теорема 8.3. (критерий оптимальности Канторовича) Если для некоторых допустимых планов  и  пары двойственных задач выполняется равенство , то планы  и  являются оптимальными планами соответствующих задач.

Теорема 8.3. (основная теорема двойственности) Если одна из двойственных задач имеет оптимальный план, то и другая разрешима, т.е. имеет оптимальный план. При этом экстремальные значения функций совпадают, т.е. . Если в одной из задач целевая функция неограниченна на множестве планов, то и в другой задаче система ограничений противоречива.

Теорема 8.4. (о дополняющей нежесткости) Для оптимальности допустимых планов и  прямой и двойственной задач необходимо и достаточно, чтобы выполнялись следующие соотношения:

                                                          (8.7)

                                                           (8.8)

где  и  - оптимальные планы соответственно прямой и двойственной задач.

Теорема 8.5. (о двойственных оценках) Компоненты оптимального плана двойственной задачи численно равны частным производным от экстремального значения целевой функции по свободным членам ограничений задачи:

                                                                     (8.9)

Еще одной из частной задач линейного программирования является задача о наиболее оптимальном (экономном) плане перевозок некоторого однородного груза от нескольких поставщиков в пункты потребления – это транспортная задача. Транспортная задача выделяется в математическом программировании своей особенностью математической модели и наличием специальных методов решения.

Стандартная транспортная задача по критерию стоимости затрат ставится следующим образом: некоторое количество пунктов отправления со своим запасом однородного товара, равного , осуществляют поставки в некоторое множество пунктов назначения. Желаемые количества груза тоже известны и равны . Известны также затраты 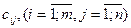 на перевозку единицы груза от каждого поставщика к любому потребителю. Необходимо составить план перевозок так, чтобы полностью удовлетворить потребности и чтобы суммарные затраты на перевозки были минимальными.

Модель транспортной задачи в которой предполагается, что суммарные запасы равны суммарным потребностям, принимает следующий вид:

f = min                                                                  (8.10)

Ограничения задачи разобьются на две подсистемы:

от каждого поставщика весь груз должен быть вывезен полностью, т.е.

 = а _i, ( i = )                                                                          (8.11)

и каждый потребитель должен получить требуемое количество груза

= b_j, ( j = )                                                                          (8.12)

по смыслу наших переменных они должны принимать неотрицательные значения исключающие обратные перевозки, т.е.

х _ij  0, ( i = , j = )                                                             (8.13)

Необходимое и достаточное условие разрешимости транспортной задачи сформулировано в следующей теореме:

Теорема 8 . 6. (о существовании допустимого плана) Для того, чтобы транспортная задача имела допустимые планы, необходимо и достаточно выполнение равенства:

                                                                                   (8.14)

Если необходимое и достаточное условие не выполняется, то ограничения (8.11) или (8.12) имеют вид неравенств типа «меньше или равно»; транспортная задача в таком случае называется открытой. Для решения открытой транспортной задачи методом по­тенциалов ее сводят к закрытой задаче путем ввода фиктивного потребителя, если в неравенства превращаются условия (8.12), или фиктивного поставщика — в случае превращения в неравенства ограничений (8.11). Причем фиктивного поставщика или фиктивного потребителя вводят на недостающее количество груза для выполнения условия (8.14).

Транспортная задача, (8.10-8.13) может быть решена, как за­дача линейного программирования с помощью симплексного метода. Однако благодаря особенностям переменных задачи и системы ограничений разработаны специальные, менее громоздкие методы ее решения, основанные на операциях сложения и вычитания.

Один из таких – метод потенциалов. Этот метод как и симплексный распадается на два этапа: на первом строится начальный опорный план, на втором – этот план последовательно улучшается с применением операции сложения и вычитания.

Наиболее применяемым методом решения таких задач на втором этапе является метод потенциалов. При котором каждой i -ой строке (i-му поставщику) соответствует потенциал u _i, который можно интерпретировать как оценку продукта в пункте поставщика. А каждому столбцу (j-му потребителю) соответствует потенциал v _j, который можно принять условно за оценку продукта в пункте потребителя. В простейшем случае транспортные расходы на доставку единицы груза равны оценке продукта в пункте потребителя плюс его оценку в пункте поставщика, т.е.

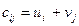                                                                                    (8.15)

Алгоритм метода потенциалов для закрытой транспортной задачи детально описан в ряде учебных пособий по математическому программированию [например, 8-10]. При решении многих оптимизационных практических задач требуется, чтобы величины (количество машин, агрегатов, оборудования, поголовья скота и др.) выражались в целых числах.

Существует класс задач в которых встречается требование целочисленности части или всех пееменных. Такие задачи получили название задач целочисленного линейного программироания (ЦЛП). Математическая модель задачи ЦЛП такая же, как и задачи линейной оптимизации, но с дополнительным требованием целочисленности всех или части неизвестных. Если требование целочисленности распространяется на часть неизвестных величин задачи, то такая задача называется частично целочисленной.

Запишем математическую модель задачи ЦЛО.

Найти экстремальное (максимальное или минимальное) значение функции, при следующих условиях:

                                                                 (8.16)

                                                                   (8.17)

                                                                          (8.18)

                                                           (8.19)        

Как мы уже знаем, экстремум для задач линейного программирования достигается в одной из крайних точек выпуклого множества. Для целочисленного линейного программирования точкой оптимума может быть любая точка области допустимых решений. Поэтому методы решения задач линейного программирования в рассмотренном ранее виде не применимы.

Если решать данную задачу симплексным методом, не учитывая условие целочисленности, то при округлении нецелых переменных оптимального плана можно получить план, далекий от оптимального или вообще не удовлетворяющий системе ограничений. Для решения задач с целочисленными переменными необходимо рассматривать особые методы решения. Такие методы целочисленной оптимизации можно разделить на три основные группы: методы отсечения; комбинаторные методы; приближенные методы.

В практических приложениях встречается большое число задач, в которых либо целевая функция, либо система ограничений (либо и та, и другая) содержит выражения, нелинейные относительно переменных. Такие задачи относятся к задачам нелинейного программирования (НЛП).

Общая задача НЛП может быть записана следующим образом:

                                                              (8.20)

                                                             (8.21)

Очевидно, что если f и g_i – линейные функции, то получаем модель задачи линейного программирования. Процесс составления математической модели задачи НЛП принципиально не отличается от составления модели задачи линейной оптимизации.

Остановимся на некоторых особенностях решения таких задач. Для решения задач НЛП существенно важно знать:

1. Выпукло или не выпукло множество допустимых решений задачи;

2. Является ли целевая функция выпуклой или вогнутой или она не относится ни к тому, ни к другому классу.

Напомним необходимые определения.

Определение 8.1. Множество выпукло, если оно вместе с любыми своими точками х₁ и х₂ содержит и все точки отрезка .

Определение 8.2. Функция f(x), определенная на выпуклом множестве X, называется выпуклой, если для любых точек и и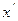з этого множества и любого  справедливо неравенство:

                                              (8.22)

Если в соотношении (8.22) при  и любых , имеет место строгое неравенство, то f(x) – строго выпукла.

Т.е. выпуклая функция f(x) на отрезке  не может принимать значений больших, чем линейная функция, интерполирующая значения  и .

Определение 8.3. Функция f(x), определенная на выпуклом множестве Х, называется вогнутой, если для любых точек и и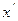з этого множества и любого  справедливо неравенство:

                                               (8.23)

Если в соотношении (8.23) при  и любых  имеет место строгое неравенство, то f(x) называется строго вогнутой.

Вогнутая функция f(x) не может принимать меньших значений, чем линейная функция, интерполирующая значения 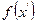 и .

Определение 8.4. Говорят, что функция , определенная на некотором замкнутом множестве Х, достигает в точке локального максимума (локального минимума), если найдется такое число , что для всех х, удовлетворяющих неравенству , выполняется неравенство  ( 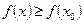).Точка x₀, в которой функция достигает локального максимума (минимума), называется точкой локального максимума (минимума).

Определение 8.5. Пусть функция  определена на замкнутом множестве X. Если и  ( ) для любой точки , то говорят, что в точке x₀ функция достигает абсолютного максимума (минимума).

Вместо термина «абсолютный» часто используют термин «глобальный». Т.е. глобальный максимум – это наибольшее значение функции в области определения. Глобальный максимум и минимум называют глобальными экстремумами функции.

В нелинейном программировании широко используется функция Лагранжа, которую всегда можно связать практически с любой задачей нелинейного программирования.

Метод множителей Лагранжа является классическим методом решения задач математического программирования, в частности выпуклого программирования.

В теории нелинейного программирования ключевое место занимает теорема Куна-Таккера.

Теорема 8.6. (теорема Куна-Таккера) Пусть существует вектор  такой, что . Тогда необходимым и достаточным условием оптимальности вектора 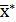, принадлежащего области допустимых решений, является существование такого вектора , что для всех  и  имеет место неравенство:

                                                         (8.24)

Теорему Куна-Таккера называют также теоремой о седловой точке. Она обобщает классический метод множителей Лагранжа на случай, когда условия связи задачи представляют собой неравенства.

Динамическое программирование – это раздел МП, в котором рассматривается теория и численные методы решения оптимизационных задач, связанных с многошаговыми (многоэтапными) процессами.

Одновременно динамическим программированием (планированием) называют математический метод оптимизации многошаговых процессов. Процессы развиваются во времени, но может быть так, что время не учитывается. Некоторые задачи решаются только динамическим методом, и решение получается гораздо шире, чем был поставлен вопрос. Основной особенностью метода динамического программирования является то, что процесс принятия решения рассматривается здесь не как единичное (одномерное) событие, а как целая серия взаимосвязанных решений. В связи с этим основной сутью метода является разбиение исходной сложной задачи на серию более простых задач аналогичного содержания. Эти мелкие задачи решаются, однако, не изолированно, а с использованием результатов других задач из этой серии. И, тем не менее, любая задача решается автономно. Очень важной особенностью метода ДП является учет на каждом шаге последствий, к которым может привести решение, принимаемое на данном шаге. Т.е. решение принимается с учетом перспективы, и всё делается так, чтобы каждый раз решение принималось с учётом того, чтобы сохранить предпосылки для принятия наилучших решений и в будущем.

Общую задачу динамического программирования можно сформулировать следующим образом: определить оптимальную стратегию , доставляющую экстремальное значение функции , где - вектор начального состояния процесса, - вектор состояния на следующем шаге, которое определяется вектором  и решением , принятым на i -ом шаге, - функция оценки, полученной на каждом шаге процесса при переходе из состояния  в состояние .

В основе вычислительных алгоритмов динамического программирования лежит следующий принцип оптимальности, сформулированный Р. Беллманом.

Принцип оптимальности (принцип Беллмана) Оптимальное поведение обладает тем свойством, что каковы бы ни были начальное состояние и начальное решение, последующие решения должны быть оптимальными относительно состояния, полученного в результате первоначального решения.

Отметим, что в параграфе приведены лишь основные сведения из математического программирования. Более подробно с методами математического программирования можно ознакомиться в работах [8-10].