 |
Главная |
Геометрические изложения и дифференцированные исчисления (построение графиков)
|
из
5.00
|
Функция 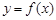 , определенная во всех точках промежутка
, определенная во всех точках промежутка 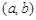 , называется возрастающей (убывающей) в этом промежутке, если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует большее (меньшее) значение функции, т. е,
, называется возрастающей (убывающей) в этом промежутке, если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует большее (меньшее) значение функции, т. е,
если 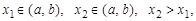 то при
то при
 – возрастающая,
– возрастающая, 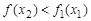 – убывающая.
– убывающая.
Из данного определения вытекает, что для возрастающей функции приращения аргумента и функции имеет один и тот же знак, в силу чего их отношение положительно: 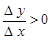 . Для убывающей функции эти приращения имеют разные знаки, в силу чего
. Для убывающей функции эти приращения имеют разные знаки, в силу чего  . Те значения аргумента, при которых функция достигает своих наибольших и наименьших по сравнению с близкими значений, называются точками максимума и минимума (точками экстремума).
. Те значения аргумента, при которых функция достигает своих наибольших и наименьших по сравнению с близкими значений, называются точками максимума и минимума (точками экстремума).
Точка 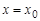 называется точкой максимума (минимума) непрерывной функции
называется точкой максимума (минимума) непрерывной функции  , а значение
, а значение 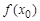 называется максимумом (минимумом) этой функции, если существует некоторая окрестность точки
называется максимумом (минимумом) этой функции, если существует некоторая окрестность точки  такая, что значение функции в любой точке этой окрестности будет меньше (больше), чем ее значение в самой точке
такая, что значение функции в любой точке этой окрестности будет меньше (больше), чем ее значение в самой точке  , т. е. меньше (больше), чем максимум (минимум)
, т. е. меньше (больше), чем максимум (минимум) 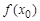 (рис. 1).
(рис. 1).
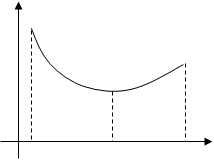
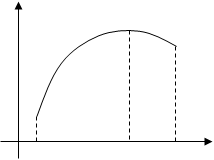 у max у
у max у
min
f(х0) f(х0)
О х0– d х0 х0+ d х О х0– d х0 х0+ d х
| точка максимума | точка минимума |
Рис. 1
Из определений точек экстремума следует, что вне d-окрестности точки экстремума поведение функции произвольно, т. е. понятия максимума и минимума функции носят характер локальных (местных), а не абсолютных понятий.
Чтобы установить признаки возрастания и убывания и признаки экстремума функций, рассмотрим ряд важных теорем математического анализа, на которые опираются все дальнейшие исследования функций.
Рекомендуется исследование функций проводить в определенной последовательности.
1. Найти область определения функции; точки разрыва и их характер; вертикальные асимптоты графика.
2. Определить возможный тип симметрии функции (четность, нечетность функции); точки пересечения графика функции с осями координат, т. е. решить уравнения 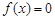 и
и 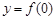 .
.
3. Найти наклонные и горизонтальные асимптоты графика функции.
4. Использовать первую производную для определения области возрастания и убывания и экстремумов функции.
5. Использовать вторую производную для определения участков выпуклости и вогнутости графика и точек перегиба.
6. Построить график функции с учетом проведенного исследования.
Пример. Провести полное исследование функции
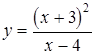
Решение:
Проведем полное исследование функции, используя следующую схему:
1. найти область определения функции;
2. исследовать на четность и нечетность функцию;
3. найти точки разрыва функции;
4. найти асимптоты (вертикальные, наклонные и горизонтальные) графика функции;
5. найти точки пересечения графика функции с координатными осями;
6. исследовать функцию на монотонность (указав интервалы возрастания и убывания) и экстремум;
7. определить интервалы выпуклости и вогнутости графика функции, точки перегиба;
8. при необходимости вычислить значения функции в дополнительных точках;
9. построить схематично график функции, используя результаты полученные в пунктах 1-8.
Областью определения функции является множество 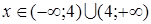 .
.
Так как 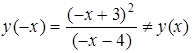 и
и 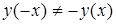 , то функция не является ни четной, ни нечетной.
, то функция не является ни четной, ни нечетной.
Функция претерпевает разрыв в точке 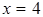 .
.
Найдем асимптоты графиков функции:
а). Прямая 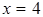 является вертикальной асимптотой, т.к.
является вертикальной асимптотой, т.к.
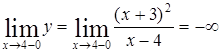 ,
, 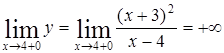
б). Находим наклонные и горизонтальные асимптоты (горизонтальные асимптоты являются частным случаем наклонных асимптот) 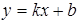 ,
,
где 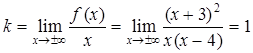 ;
;
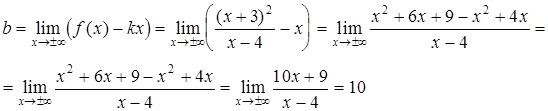
Таким образом, прямая 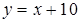 является единственной наклонной асимптотой и на
является единственной наклонной асимптотой и на 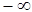 , и на
, и на 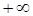 .
.
Найдем точки пересечения графика функции с осями координат.
а) С осью  :
: 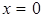 ,
, 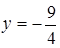 , т.е. точка пересечения с осью
, т.е. точка пересечения с осью  -
- 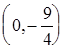 .
.
б) С осью 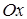 :
: 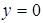 ,
, 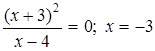 , т.е. точка пересечения с осью
, т.е. точка пересечения с осью 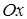 -
- 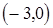 .
.
6. Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции.
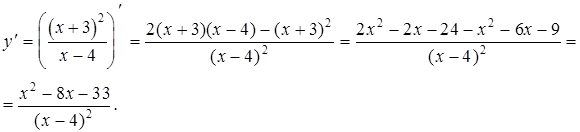
Из 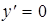 получаем
получаем  , откуда
, откуда  ,
, 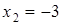 .
.
+ _ +
______________________________________ x
-3 11
Так как на интервалах 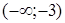 и
и 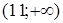 производная положительна, т.е.
производная положительна, т.е. 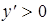 , то график функции на указанных интервалах возрастает. Так как на интервале
, то график функции на указанных интервалах возрастает. Так как на интервале 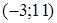 производная отрицательна, т.е.
производная отрицательна, т.е.  , то на указанном интервале график функции убывает.
, то на указанном интервале график функции убывает.
Так как при переходе через точки  ,
, 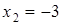 производная функции меняет знаки и эти точки входят в область определения функции, то
производная функции меняет знаки и эти точки входят в область определения функции, то  ,
, 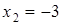 - точки локального экстремума. Причем
- точки локального экстремума. Причем 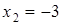 точка локального минимума:
точка локального минимума: 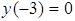 (так как при переходе через нее производная меняет знак с "+" на "-");
(так как при переходе через нее производная меняет знак с "+" на "-");  - точка локального максимума:
- точка локального максимума: 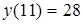 (так как при переходе через нее производная меняет знак с "-" на "+").
(так как при переходе через нее производная меняет знак с "-" на "+").
7. Исследуем график функции на выпуклость, вогнутость и определим точки перегиба. Для этого найдем вторую производную функции.
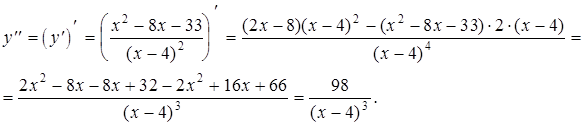
Очевидно, что в интервале  вторая производная меньше нуля, т.е.
вторая производная меньше нуля, т.е. 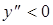 , и в этом интервале график функции является выпуклым вверх. В интервале
, и в этом интервале график функции является выпуклым вверх. В интервале 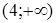 вторая производная больше нуля, т.е.
вторая производная больше нуля, т.е. 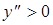 , и в этом интервале график функции является выпуклым вниз (вогнутым).
, и в этом интервале график функции является выпуклым вниз (вогнутым).
Несмотря на то, что при переходе через точку 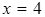 вторая производная меняет знак, она не является точкой перегиба, так как
вторая производная меняет знак, она не является точкой перегиба, так как 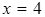 не входит в область определения функции, т.е. функция в ней не определена. Таким образом, точек перегиба у графика функции нет.
не входит в область определения функции, т.е. функция в ней не определена. Таким образом, точек перегиба у графика функции нет.
Из 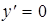 получаем
получаем 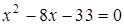 , откуда
, откуда 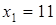 ,
, 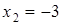 .
.
+ _ +
______________________________________ x
-3 11
Так как на интервалах 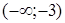 и
и 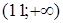 производная положительна, т.е.
производная положительна, т.е. 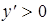 , то график функции на указанных интервалах возрастает. Так как на интервале
, то график функции на указанных интервалах возрастает. Так как на интервале 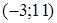 производная отрицательна, т.е.
производная отрицательна, т.е.  , то на указанном интервале график функции убывает.
, то на указанном интервале график функции убывает.
Так как при переходе через точки 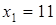 ,
, 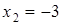 производная функции меняет знаки и эти точки входят в область определения функции, то
производная функции меняет знаки и эти точки входят в область определения функции, то 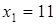 ,
, 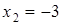 - точки локального экстремума. Причем
- точки локального экстремума. Причем 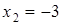 точка локального минимума:
точка локального минимума: 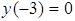 (так как при переходе через нее производная меняет знак с "+" на "-");
(так как при переходе через нее производная меняет знак с "+" на "-"); 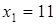 - точка локального максимума:
- точка локального максимума: 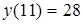 (так как при переходе через нее производная меняет знак с "-" на "+").
(так как при переходе через нее производная меняет знак с "-" на "+").
|
из
5.00
|
Обсуждение в статье: Геометрические изложения и дифференцированные исчисления (построение графиков) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

