 |
Главная |
Функции нескольких переменных, дифференцированных исчислений
|
из
5.00
|
До сих пор рассматривались функции 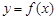 одной переменной х. В случае зависимости параметров какого-то процесса или явления от многих факторов вводится понятие функции нескольких переменных.
одной переменной х. В случае зависимости параметров какого-то процесса или явления от многих факторов вводится понятие функции нескольких переменных.
Пусть каждому набору значений n переменных величин 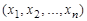 из множества M , называемых независимыми переменными, по какому-либо закону ставится в соответствие некоторое число z, называемое зависимой переменной. Тогда говорят, что задана функция нескольких переменных
из множества M , называемых независимыми переменными, по какому-либо закону ставится в соответствие некоторое число z, называемое зависимой переменной. Тогда говорят, что задана функция нескольких переменных 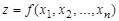 .
.
 z
z 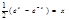 y
O
x
M
Рис. 3
y
O
x
M
Рис. 3
| Функция одной переменной 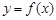 изображается на плоскости в виде линии. В случае двух переменных область определения M функции изображается на плоскости в виде линии. В случае двух переменных область определения M функции 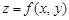 представляет собой некоторое множество точек на координатной плоскости О xy и тогда графиком функции является некоторая поверхность (рис. 3). представляет собой некоторое множество точек на координатной плоскости О xy и тогда графиком функции является некоторая поверхность (рис. 3).
|
Приведем примеры функций нескольких переменных.
1. Функция вида 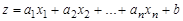 , где
, где 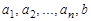 – постоянные числа, называется линейной или гиперплоскостью
– постоянные числа, называется линейной или гиперплоскостью 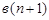 -мерном пространстве.
-мерном пространстве.
2. Функция вида 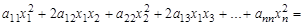
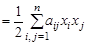 , где
, где 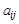 – постоянные числа, называется квадратичной формой от переменных
– постоянные числа, называется квадратичной формой от переменных 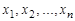 .
.
При рассмотрении функций в n-мерном пространстве широко используется геометрический язык, хотя буквальное понимание геометрических терминов возможно только при п = 2 и п = 3.
Далее для наглядности будем рассматривать функции двух переменных ( 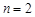 ), хотя практически все понятия и теоремы, сформулированные для
), хотя практически все понятия и теоремы, сформулированные для 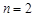 , переносятся на случай
, переносятся на случай 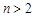 . Основные понятия математического анализа, введенные для функции одной переменной, переносятся на случай двух переменных. Так, число А называется пределом функции
. Основные понятия математического анализа, введенные для функции одной переменной, переносятся на случай двух переменных. Так, число А называется пределом функции 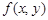 в точке
в точке 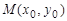 , если для любого числа
, если для любого числа 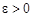 можно найти число
можно найти число 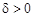 такое, что для всех точек
такое, что для всех точек 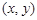 из d-окрестности точки М выполняется неравенство
из d-окрестности точки М выполняется неравенство 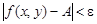 . Для обозначения предела функции в точке используется символика
. Для обозначения предела функции в точке используется символика
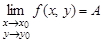 .
.
Окрестностью точки 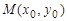 называется круг, содержащий точку М.
называется круг, содержащий точку М.
В случае функции двух переменных аргумент может стремиться к предельной точке по различным направлениям на плоскости, поэтому следует говорить о пределах функции в точке вдоль определенных линий.
Функция 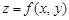 называется непрерывной в точке
называется непрерывной в точке 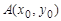 , если предел функции в этой точке существует и равен значению функции в этой точке, т. е.
, если предел функции в этой точке существует и равен значению функции в этой точке, т. е. 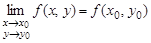 . Геометрический смысл непрерывности функции при
. Геометрический смысл непрерывности функции при 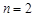 очевиден: график функции
очевиден: график функции 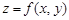 представляет собой в точке непрерывности
представляет собой в точке непрерывности 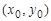 сплошную поверхность в некоторой окрестности этой точки.
сплошную поверхность в некоторой окрестности этой точки.
Пример. Найти экстремум функции двух переменных z = x2 + y2, x Î [-20, 20], y Î [-10, 10].
Решение.
Необходимое условие экстремума 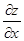 = 2х = 0,
= 2х = 0, 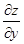 = 2у = 0, откуда координаты стационарной точки (хст, уст) = (0, 0).
= 2у = 0, откуда координаты стационарной точки (хст, уст) = (0, 0).
Вторые производные А = 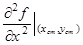 = 2; В =
= 2; В = 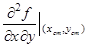 = 0; С =
= 0; С = 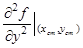 = 2. Так как AC - B2 = 4 > 0, то в точке (0, 0) — локальный минимум.
= 2. Так как AC - B2 = 4 > 0, то в точке (0, 0) — локальный минимум.
Значение функции в точке минимума z (0, 0) = 0.
Литература:
1. Выгодский М.Я. Справочник по высшей математике. - М.: Джангар, 2000. - 864 с.
2. Гордон В.А., Шмаркова Л.И. Краткий курс математики / Учебное пособие. – Орёл: ОрёлГТУ, 2000. – 96 с.
3. Демидович Б.П. Сборник задач и упражнений по математическому анализу: М.: Наука, 1972.
|
из
5.00
|
Обсуждение в статье: Функции нескольких переменных, дифференцированных исчислений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

