 |
Главная |
Базисы векторного геометрического пространства
|
из
5.00
|
1. Базис векторов прямой. Множество V1 векторов фиксированной прямой образует векторное пространство.
Теорема 1. Любой ненулевой вектор e прямой образует базис векторного пространства V1.
Доказательство. По свойству 3 § 2 вектор e образует линейно независимую систему. Пусть a Î V1. Тогда по свойству линейной зависимости вектор a линейно выражается через вектор e. По определению 1 вектор e образует базис пространства V1.
Теорема 2. Векторы a и b коллинеарны тогда только тогда, когда они линейно зависимы.
Доказательство. Пусть вектора a и b коллинеарны. Если a = 0, то по свойству 3 § 3 вектора a,b линейно зависимы. Если a ¹ 0, по теореме о линейной зависимости систем векторов вектор b линейно выражается через вектор a , и векторы a,b линейно зависимы.
Обратно, если векторы a,b линейно зависимы, то по свойству 1 § 3, один из этих векторов линейно выражается через другой и вектора a и b коллинеарны.
Следствие 1. Векторы a и b коллинеарны тогда только тогда, когда они линейно зависимы.
Векторы a и b неколлинеарны тогда только тогда, когда они линейно независимы.
В силу предложений, полученных в предыдущем параграфе, получаем следующие следствия.
Следствие 2. Векторы a = (a1, a2,... ,an), b = (b1, b2,... ,bn)неколлинеарны тогда только тогда, когда ранг матрицы
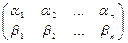 , (12)
, (12)
составленной из координат векторов, равен 2. Векторы a и b коллинеарны тогда и только когда ранг матрицы (12) равен 1.
Ранг матрицы (12) равен 1 тогда и только тогда, одна из строк матрицы получается из другой строки, умножением на одно и то же число. Поэтому получаем еще следующее утверждение.
Следствие 2. Векторы a = (a1, a2,... ,an), b = (b1, b2,... ,bn)неколлинеарны тогда только тогда, когда координаты векторов соответственно пропорциональны, т.е.
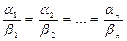 , (13)
, (13)
 где предполагается, что числитель равен нулю, если знаменатель равен нулю.
где предполагается, что числитель равен нулю, если знаменатель равен нулю.
2. Базис векторов на плоскости. Множество V2 векторов фиксированной плоскости образует векторное пространство.
Теорема 3. Любая упорядоченная система двух неколлинеарных векторов a, b Î V2 образуют базис векторного пространства V2.
Доказательство. Пусть a и b неколлинеарные вектора плоскости. По следствию 2 теоремы 2 векторы a и b образует линейно независимую систему. Пусть с Î V2. Отложим векторы a, b и с от точки O: a = 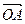 , b =
, b = 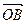 и с =
и с = 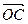 (см. рис. 17). Проведем через точку C прямую l, параллельную прямой OB. Так как векторы a и b неколлинеарны, то прямые OA и l пересекаются в точке D. Тогда
(см. рис. 17). Проведем через точку C прямую l, параллельную прямой OB. Так как векторы a и b неколлинеарны, то прямые OA и l пересекаются в точке D. Тогда 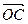 =
= 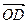 +
+ 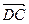 . Так как векторы
. Так как векторы 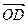 и
и 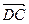 соответственно коллинеарны векторам a и b, то по свойству линейной зависимости они соответственно линейно выражается через векторы a и b:
соответственно коллинеарны векторам a и b, то по свойству линейной зависимости они соответственно линейно выражается через векторы a и b: 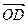 =a a,
=a a, 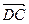 =b b. Поэтому с =
=b b. Поэтому с = 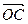 = a a + b b, и по определению 1 вектора a и b образует базис пространства V2.
= a a + b b, и по определению 1 вектора a и b образует базис пространства V2.
По теореме 3 базис векторов на плоскости образуют любые два неколлинеарные вектора, поэтому любой вектор на плоскости имеет две координаты. Тогда справедливо следующее утверждение.
Следствие 1. Вектора a = (a1, b1), b = (a2, b2)образуют базис векторов плоскости тогда и только тогда, когда
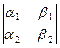 = 0.
= 0.
Теорема 4. Векторы a, b и с компланарны тогда только тогда, когда они линейно зависимы.
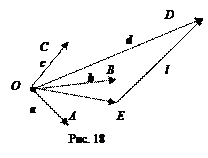 Доказательство. Пусть вектора a, b и с компланарны. По определению они могут быть изображены на одной плоскости p. Если вектора a,b коллинеарны, то по следствию 1 теоремы 2 они линейно зависимы. Тогда по свойству по свойству линейной зависимости вектора a, b, с линейно зависимы. Если вектора a,b неколлинеарны, то по теореме 3 они образуют базис векторов плоскости p. Тогда вектор с линейная комбинация векторов a, b, и по свойству линейной зависимости векторы a, b, с линейно зависимы.
Доказательство. Пусть вектора a, b и с компланарны. По определению они могут быть изображены на одной плоскости p. Если вектора a,b коллинеарны, то по следствию 1 теоремы 2 они линейно зависимы. Тогда по свойству по свойству линейной зависимости вектора a, b, с линейно зависимы. Если вектора a,b неколлинеарны, то по теореме 3 они образуют базис векторов плоскости p. Тогда вектор с линейная комбинация векторов a, b, и по свойству линейной зависимости векторы a, b, с линейно зависимы.
Обратно, если векторы a,b, с линейно зависимы, то по свойству линейной зависимости, один из этих векторов линейно выражается через два другие. Тогда вектора могут быть изображены одной плоскости и поэтому коллинеарны.
Следствие 1. Векторы a, b и с некомпланарны тогда только тогда, когда они линейно независимы.
3. Базис векторов пространства. Рассмотрим множество V3 всех векторов пространства.
Теорема 5. Любая упорядоченная система трех некомпланарных векторов a, b, с Î V3 образуют базис векторного пространства V3.
Доказательство. Пусть a, b, с некомпланарные векторы. По следствию 1 теоремы 8 они образует линейно независимую систему. Пусть d Î V3. Отложим векторы a, b, с и d от точки O: a = 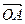 , b =
, b = 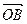 , с =
, с = 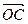 , d =
, d = 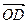 (см. рис. 18). Проведем через точку D прямую l, параллельную прямой OD. Так как векторы a, b, с некомпланарны,
(см. рис. 18). Проведем через точку D прямую l, параллельную прямой OD. Так как векторы a, b, с некомпланарны,  то прямая l пересекает плоскость OAB в точке E. Тогда
то прямая l пересекает плоскость OAB в точке E. Тогда 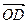 =
= 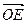 +
+ 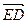 . Так как векторы
. Так как векторы 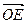 лежит в плоскости OAB, а вектора образуют базис векторов этой плоскости, то по теореме 7
лежит в плоскости OAB, а вектора образуют базис векторов этой плоскости, то по теореме 7 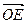 = a a + b b, где a, b Î R. Так как вектор
= a a + b b, где a, b Î R. Так как вектор 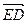 коллинеарен вектору c , то по теореме 8 § 1 он линейно выражается через вектор с:
коллинеарен вектору c , то по теореме 8 § 1 он линейно выражается через вектор с: 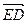 = g с. Поэтому d =
= g с. Поэтому d = 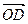 = a a + b b + g с и по определению 1 вектора a, b, с образует базис пространства V3.
= a a + b b + g с и по определению 1 вектора a, b, с образует базис пространства V3.
По теореме 5 базис векторов на пространстве образуют любые три некомпланарные вектора, поэтому любой вектор в пространстве имеет три координаты. Тогда справедливо следующее утверждение.
Следствие 1. Вектора a = (a1, b1, g1), b = (a2, b2, g2), с = (a3, b3, g3)образуют базис векторов пространства тогда и только тогда, когда
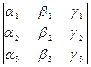 = 0.
= 0.
Теорема 6. Любые четыре вектора a, b, с, d в пространстве линейно зависимы.
Доказательство. Если векторы a, b, с компланарны, то по теоремы 5 они линейно зависимы. Тогда по свойству линейной зависимости по свойству 4 § 3 вектора a, b, с, d линейно зависимы. Если вектора a, b, с некомпланарны, то по теореме 5 они образуют базис векторов пространства. Тогда вектор d линейная комбинация векторов a, b, с и по свойству линейной зависимости векторы a, b, с, d линейно зависимы.
Задача 1. Доказать что векторы a = (1, 2, 0), b = (3, 2, 1), с = (0, 1, -1) образуют базис в пространстве и выразить вектор d = (5, 5, 2) через векторы базиса.
Решение. Так как определитель
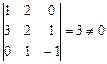 ,
,
то векторы a, b, с образуют базис пространства V3.
Для того, чтобы найти координаты вектора d в базисе a, b, с составим векторное уравнение
x a + y b + z c = 0. (14)
и запишем его в координатной форме:
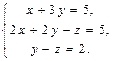
Решаем эту систему линейных уравнений: x = 2, y = 2, z = -1 и находим d = 2a + b - с.
Координаты вектора.
Теорема 1. Любой вектор a Î V единственным образом линейно выражается через вектора базиса, т.е., если v1, v2, ..., vn базис векторного пространства V , то
a = x1v1 + x2v2 +...+ xnvn ; x1, x2, ...,xn Î P, (2)
и такое представление единственно.
Доказательство. 6° Пусть b1, b2, ..., br базис системы S. По определению базиса любой вектор a Î S есть линейная комбинация векторов базиса:
a = a1b1 + a2b2 +...+ arbr.
Доказывая единственность такого представления, допустим противное, что есть еще одно представление:
a = b1b1 + b2b2 +...+ brbr.
Вычитая эти равенства почленно, находим
0 = (a1 - b1)b1 + (a2 - b2)b2 +...+ (ar - br)br.
Так как базис b1, b2, ..., br линейно независимая система, то все коэффициенты ai - bi =0; i = 1, 2, ..., r. Следовательно, ai = bi ; i = 1, 2, ..., r и единственность доказана.
Представление вектора a в виде (2) называется разложением вектора по векторам базиса, а числа x1, x2, ..., xn называются координатами вектора a в данном базисе.
По определению произведения строки на столбец это равенство можно представить как
a = (v1 ,v2 ,... vn) 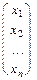 = v ×(x1 ,x2 ,... ,xn)t, (3)
= v ×(x1 ,x2 ,... ,xn)t, (3)
v = (v1 ,v2 ,... vn) - базис векторного пространства. Строка (x1 ,x2 ,... ,xn) называется координатной строкой вектора a, и вектор записывается в виде: a = (a1, a2,... ,an). Столбец (x1 ,x2 ,... ,xn)t - координатным столбцом вектора a.
Теорема 2. Пусть два вектора a и b разложены по одному и тому же базису: a = (a1, a2,... ,an), b = (b1, b2,... ,bn). Тогда справедливы утверждения.
1° Векторы a и b равны тогда и только тогда, когда равны их соответствующие координаты, т.е. ai = bi ; i = 1, 2,… , n .
2° При сложении векторов складываются их соответствующие координаты, т.е. a + b = (a1 + b1,a2 + b2,... ,an + bn).
3° При умножении вектора a на число l все координаты вектора a умножаются на это число l , т.е. l a = (l a1,l a2,... , l an).
Доказательство. Справедливость 1° следует в силу единственности разложения вектора по векторам базиса. Докажем 2°. Пусть
a = x1v1 + x2v2 +...+ xnvn , b = y1v1 + y2v2 +...+ ynvn
разложения векторов a , b по базису v1 ,v2 ,... vn. Тогда
a + b = (x1 + y1)v1 + (x2 + yn)v2 +...+ (xn + yn)vn
и отсюда следует 2°. Утверждение 3° доказывается аналогично.
3. Матрица перехода. Пусть
v = (v1, v2, ..., vn) ,
u = (u1, u2, ..., un)
два базиса векторного пространства V . Выразим вектора базиса второго базиса через вектора первого базиса:
u1 = t11v1 + t21v2 + ... +tn1vn,
u2 = t12v1 + t22v2 + ... +tn2vn, (4)
. . . . . . . . . . . . . .
un = t1nv1 + t2nv2 + ... +tnnvn.
Определение 3. Матрицей перехода от базиса v , к базису u называется такая матрица
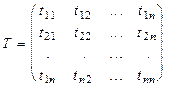 ,
,
столбцы которой есть соответствующие координатные столбцы векторов второго базиса u в первом базисе v.
В силу (4) связь между базисами и матрицей перехода можно записать в виде:
(u1, u2, ..., um) = (v1, v2, ..., vn) 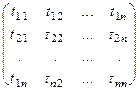 ,
,
или
u = vT. (5)
C другой стороны, если T ¢ - матрица перехода от базиса u к базису v , то
v = uT ¢. (6)
Из (5) и (6) получаем
u = (uT ¢)T = u(T ¢ T) , v = (vT)T ¢ = v (TT ¢). (7)
Лемма 1. Пусть А, В матрицы размерности m ´ n c элементами из поля Р и v = (v1, v2, ..., vn) - базис n-мерного векторного пространства на Р. Если vA = vB, то A = B.
Доказательство. Пусть
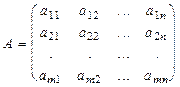 ,
, 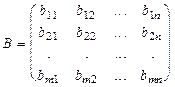 .
.
Тогда по определениям умножения и равенства матриц равенство vA = vB запишется в виде m векторных равенств:
a1jv1 + a2jv2 + ... + anjvn = b1jv1 + b2jv2 + ... + bnjvn; j = 1, 2, ...,m.
В силу условия равенства векторов, записанных в координатной форме находим aij = bij; i = 1, 2, ...,n; j = 1, 2, ...,m. Отсюда A = B. Лемма доказана.
Так как v = vЕ и u = uE , то из равенств (7) по лемме 1 получаем T ¢ T = TT ¢ = Е. Отсюда detT ¹ 0 , T ¢ = T-1 и доказана теорема.
Теорема 3. Матрица перехода от одного базиса к другому является невырожденной матрице. Матрицы перехода от первого базиса ко второму и от второго базиса к первому базису являются взаимно обратными матрицами.
4. Преобразование координат вектора. Найдем связь между координатными столбцами произвольного вектора a в базисах v и u. Пусть (x1 ,x2 ,... ,xn)t и (x1¢ ,x2¢ ,... ,xn¢)t - координатные столбцы вектора a в базисах v и u . Тогда по формуле (3)
a = v ×(x1 ,x2 ,... ,xn)t , a = u ×(x1¢ ,x2¢ ,... ,xn¢)t .
Отсюда по формуле (6) находим
a = v ×(x1 ,x2 ,... ,xn)t = (uT)×(x1¢ ,x2¢ ,... ,xn¢)t =u(T ×(x1¢ ,x2¢ ,... ,xn¢)t)
и по лемме 1
(x1 ,x2 ,... ,xn)t = T ×(x1¢ ,x2¢ ,... ,xn¢)t . (8)
Отсюда по определению равенства матриц получаем систему равенств:
x1 = t11x1¢ + t12x2¢ + ... + t1nxn¢,
x2 = t21x1¢ + t22x2¢ + ... + t2nxn¢,
. . . . . . . . . . . . . . . . (9)
xn = tn1x1¢ + tn2x2¢ + ... + tnnxn¢.
Полученные формулы (8) или (9) называются формулами преобразования координат, а матрица T так же называется матрицей преобразования координат.
5. Условие линейной независимости векторов в координатной форме. Рассмотрим систему векторов ai = a i1v1 + a i2v2 + ... +a i nvn, i =1, 2, …, k. Составим векторное уравнение
x1a1 +x2a2 + ...+ xkak = 0. (10)
В силу условия равенства векторов координатной форме уравнение (10) равносильно системе n линейных уравнений с k неизвестными:
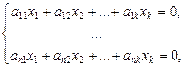 (11)
(11)
Система (11) имеет нулевое решение. По теореме Кронекера-Капелли она имеет единственное нулевое решение тогда и только тогда, когда ранг матрицы системы равен k . Отсюда получаем следующую теорему.
Теорема 4. Система k векторов n -мерного векторного пространства линейно независима тогда и только тогда, когда ранг матрицы, составленной из координат этих векторов в некотором базисе, равен k .
Следствие 1. Упорядоченная система из n векторов образует базис n -мерного векторного пространства тогда и только тогда, когда ранг матрицы, составленной из координат этих векторов в некотором базисе, равен n .
Ранг квадратной матрицы порядка равен тогда и только тогда, когда определитель матрицы не равен нулю. Таким образом получаем следующее утверждение.
Следствие 2. Упорядоченная система из n векторов образует базис n -мерного векторного пространства тогда и только тогда, когда равен нулю определитель, составленной из координат этих векторов в некотором базисе.
|
из
5.00
|
Обсуждение в статье: Базисы векторного геометрического пространства |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

