 |
Главная |
Задачи, решаемые методом информационного параметра
|
из
5.00
|
Метод информационного параметра применяется для построения математических моделей различных радиосистем и радиоустройств, в которых осуществляются преобразования информационного параметра. Особенно широко этот метод используется при формировании математических моделей радиозвеньев следящего типа, и в частности:
- радиоустройств измерения параметров движения объектов (дальности, скорости, направления, местоположения и т.п.);
- РЛС слежения за целью, систем радиоуправления (самонаведения);
- систем автоматического слежения в радиоприёмном устройстве за фазой (ФАП), частотой (ЧАП, ФАПЧ);
- оптимальных и квазиоптимальных демодуляторов.
Большинство подобных радиосистем и радиоустройств одноканального типа с одним сигнальным входом могут быть представлены в виде обобщённой схемы (рис. 1)
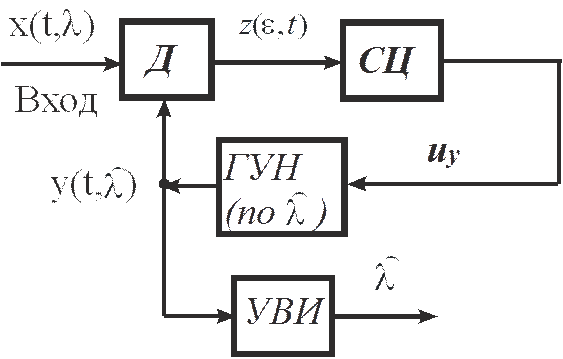
Рис. 1.
Здесь информационным параметром λ(t), за которым следит схема, является любой из параметров – амплитуда, частота, фаза, групповое время запаздывания и др. Измеренным (отслеженным) параметром является оценка 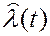 , являющаяся информационным параметром опорного радиосигнала y[t,
, являющаяся информационным параметром опорного радиосигнала y[t, 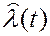 ], вырабатываемого в процессе слежения генератором, управляемым напряжением (ГУН) uу(t) по параметру
], вырабатываемого в процессе слежения генератором, управляемым напряжением (ГУН) uу(t) по параметру 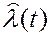 . Напряжение uу(t) формируется с помощью дискриминатора (Д) и линейной сглаживающей цепи (СЦ). В случае необходимости устройство выделения информации (УВИ) вырабатывает оценку из напряжения ГУН. В качестве примера на рис. 2, а показана типовая схема ФАП (ФАПЧ), следящая за полной фазой Ф(t)=ω0t-Ψ(t) или мгновенной частотой ωмгн(t)=dФ(t)/dt=ω0-dΨ(t)/dt входного радиосигнала, где роль дискриминатора исполняет БНРЗ – фазовый дискриминатор (ФД) типа коррелятора.
. Напряжение uу(t) формируется с помощью дискриминатора (Д) и линейной сглаживающей цепи (СЦ). В случае необходимости устройство выделения информации (УВИ) вырабатывает оценку из напряжения ГУН. В качестве примера на рис. 2, а показана типовая схема ФАП (ФАПЧ), следящая за полной фазой Ф(t)=ω0t-Ψ(t) или мгновенной частотой ωмгн(t)=dФ(t)/dt=ω0-dΨ(t)/dt входного радиосигнала, где роль дискриминатора исполняет БНРЗ – фазовый дискриминатор (ФД) типа коррелятора.
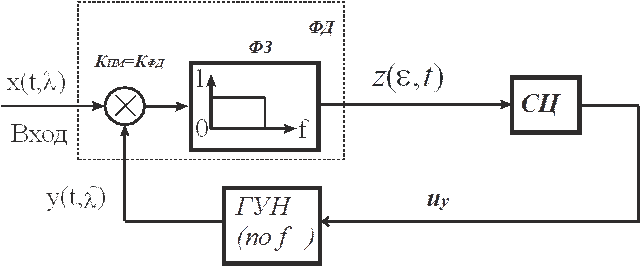
Рис. 2, а.

Рис. 2, б.
В схемах ФАПЧ обычно ГУН управляется не по фазе, а по частоте. Вариант схемы ФАП (ФАПЧ), работающей по промежуточной частоте (рис. 2, б), состоит из преобразователя частоты (ПЧ), УПЧ и собственно фазового дискриминатора (ФД) с автономным гетеродином (АГ) промежуточной частоты. Подобная схема является основой автоматических селекторов частоты («скорости») в следящих РЛС.
К следящим схемам (рис. 1) сводятся оптимальные демодуляторы (ОДМ), синтезируемые в постановке задачи Ван-Триса (рис. 3). Задачей оптимального демодулятора является формирование оптимальных оценок  ,
, 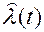 (в рамках выбранного критерия оптимальности) сигнала (сообщения)
(в рамках выбранного критерия оптимальности) сигнала (сообщения) 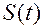 и информационного параметра
и информационного параметра 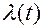 из смеси
из смеси 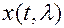 модулированного сигнала
модулированного сигнала 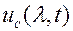 и шума
и шума  . При этом постулируется линейная связь функций
. При этом постулируется линейная связь функций 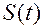 и
и 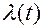 с помощью линейного фильтра с импульсной характеристикой
с помощью линейного фильтра с импульсной характеристикой  .
.
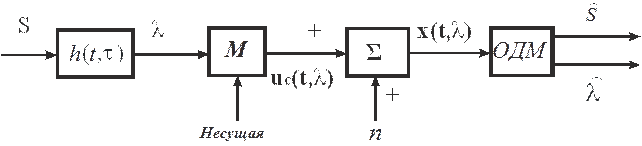
Рис. 3.
Структурная схема оптимального демодулятора для случая белого гауссовского шума 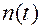 с нестационарной спектральной плотностью
с нестационарной спектральной плотностью 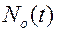 и гауссовских процессов
и гауссовских процессов 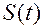 и
и 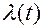 с заданной корреляционной функцией
с заданной корреляционной функцией 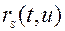 (рис. 4, а) состоит из оптимального дискриминатора (ОД), ГУН и оптимального линейного фильтра (ОЛФ) с импульсной характеристикой
(рис. 4, а) состоит из оптимального дискриминатора (ОД), ГУН и оптимального линейного фильтра (ОЛФ) с импульсной характеристикой
h0(t,t-τ)=ω(t,u)=rS(t,u), (1)
принципиально не реализуемого. Оптимальные оценки  ,
, 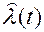 разделены тем же фильтром с импульсной характеристикой
разделены тем же фильтром с импульсной характеристикой  , что и в схеме рис. 3. Оптимальный дискриминатор, как видно из рис. 4, б, работает от двух опорных напряжений, вырабатываемых ГУН:
, что и в схеме рис. 3. Оптимальный дискриминатор, как видно из рис. 4, б, работает от двух опорных напряжений, вырабатываемых ГУН:
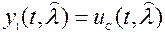 ;
; 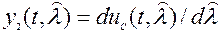 , (2)
, (2)
где 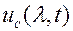 - радиосигнал в смеси.
- радиосигнал в смеси.
Теория оптимальных демодуляторов с текущей оценкой по байесовскому критерию при гауссовском шуме n(t) и параметре 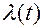 при аддитивной смеси была развита сов. учёными. Схемы оптимального дискриминатора и генератора таких оптимальных демодуляторов (рис. 5, а) не отличаются от схем на рис. 4,а,б. Всё отличие в оптимальном линейном фильтре, управляемом (адаптивном) и реализуемом. Для этого в специальном блоке точности (БТ) от трёх опорных радиосигналов ГУН (рис. 5,б)
при аддитивной смеси была развита сов. учёными. Схемы оптимального дискриминатора и генератора таких оптимальных демодуляторов (рис. 5, а) не отличаются от схем на рис. 4,а,б. Всё отличие в оптимальном линейном фильтре, управляемом (адаптивном) и реализуемом. Для этого в специальном блоке точности (БТ) от трёх опорных радиосигналов ГУН (рис. 5,б)
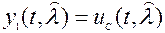 ;
; 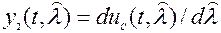 ;
; 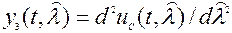
на выходе усилителя с коэффициентом усиления K(t)=2/N0(t) формируется управляющая функция p(t).
Существует и третье направление оптимальных демодуляторов (Р.Л. Стратонович, В.И. Тихонов и др.) при допущении марковости шума n(t) и параметра 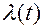 с формированием оптимальных оценок по текущей апостериорной плотности вероятностей. Решения здесь несколько отличаются от вышеописанных в основном схемой оптимального линейного фильтра.
с формированием оптимальных оценок по текущей апостериорной плотности вероятностей. Решения здесь несколько отличаются от вышеописанных в основном схемой оптимального линейного фильтра.
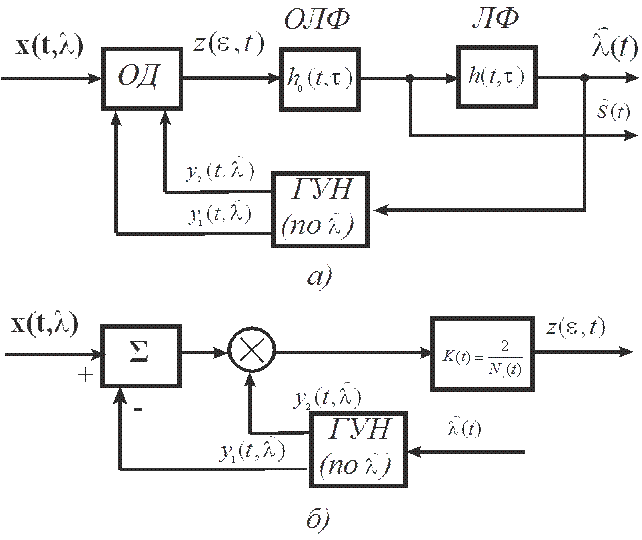
Рис. 4 а, б.
Сущность метода информационного параметра
Сущность метода информационного параметра, являющегося одним из основных методов математического моделирования следящих радиосистем и радиоустройств (рис. 1), заключается в их замене петлёй автоматического регулирования (рис. 7) с входным воздействием в виде информационного параметра 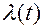 . Рассмотрим этапы решения подобной задачи математического моделирования:
. Рассмотрим этапы решения подобной задачи математического моделирования:
1) Замена входной смеси 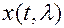 информационным параметром
информационным параметром 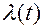 , а в двухцелевой ситуации двумя параметрами
, а в двухцелевой ситуации двумя параметрами 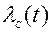 ,
, 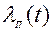 ;
;
2) Замена дискриминатора его статистическим эквивалентом (СЭ);
3) Замена ГУН низкочастотной моделью;
4) Составление математического описания петли автоматического регулирования (рис. 7) с дальнейшим переводом полученных алгоритмов на цифровую модель.
При выполнении вышеуказанных этапов сглаживающая цепь (СЦ) остается без изменений, как и в реальной схеме. На этапе 4 применяют следующие способы математического описания моделей на рис. 7.:
а) интегральные (интегродифференциальные) уравнения – каждое звено
описывается временными методами, что позволяет получить систему интегродифференциальных уравнений;
б) дифференциальные уравнения – исходя из первого способа (или другими методами) можно найти дифференциальное уравнение высокого порядка, описывающее схему модели типа на рис 7;
в) предварительное упрощение.
В теории автоматического регулирования разработано много способов исследования (временные, частотные) петлей слежения типа на рис. 7 (способы линеаризации и др.), которые можно использовать для предварительного упрощения математического описания модели.
Модель на рис. 7, являющаяся универсальной для всех следящих радиосистем и радиоустройств, позволяет осуществлять их моделирование с единых позиций. Значение подобных универсальных моделей в задачах исследования порой весьма сложных радиосистем трудно переоценить. Главным вопросом математического моделирования является обеспечение статистической адекватности на рис. 7 и реальной следящей схемы на рис. 1. Обычно удовлетворяются идентичностью дифференциальных уравнений по оценке 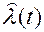 или сигналу ошибки
или сигналу ошибки  .
.
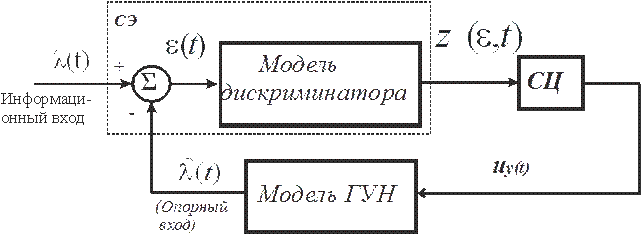
Рис. 7.
|
из
5.00
|
Обсуждение в статье: Задачи, решаемые методом информационного параметра |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

