 |
Главная |
Геометрическая интерпретация устойчивости по Ляпунову
|
из
5.00
|
Геометрическую интерпретацию устойчивости по Ляпунову удобно продемонстрировать на динамической системе второго порядка
 (6.6)
(6.6)
Представим, что операторы  имеют следующий вид
имеют следующий вид
 (6.7)
(6.7)
Характеристическое уравнение (6.6) с учетом (6.7) будет следующим
 . (6.8)
. (6.8)
Пусть  , тогда корни уравнения (7.8) будут комплексно-сопряженными с отрицательной вещественной частью, т.е.
, тогда корни уравнения (7.8) будут комплексно-сопряженными с отрицательной вещественной частью, т.е.  , где
, где  (
(  всегда положительно). Движения (фазовые траектории), характерные для таких корней представлены на рисунке 6.1. Выполняются условия Ляпунова (6.4) и (6.5) - все фазовые траектории сходятся к состоянию равновесия. Такое состояние равновесия называется «устойчивый фокус» (асимптотически устойчивое состояние равновесия).
всегда положительно). Движения (фазовые траектории), характерные для таких корней представлены на рисунке 6.1. Выполняются условия Ляпунова (6.4) и (6.5) - все фазовые траектории сходятся к состоянию равновесия. Такое состояние равновесия называется «устойчивый фокус» (асимптотически устойчивое состояние равновесия).
Примечание. Названия состояниям равновесия для динамических систем второго порядка дал А.Пуанкаре. В настоящее время существует классификация состояний равновесия (особых точек) вплоть до систем четвертого порядка.

Рисунок 6.1 - Состояние равновесия типа «устойчивый фокус»
Пусть  , тогда корни уравнения (6.8) будут комплексно-сопряженными с положительной вещественной частью, т.е.
, тогда корни уравнения (6.8) будут комплексно-сопряженными с положительной вещественной частью, т.е.  , где
, где  . Движения (фазовые траектории), характерные для таких корней представлены на рисунке 6.2. Не выполняется условие Ляпунова (6.4) - все фазовые траектории направлены от состояния равновесия. Такое состояние равновесия называется «неустойчивый фокус» (неустойчивое состояние равновесия).
. Движения (фазовые траектории), характерные для таких корней представлены на рисунке 6.2. Не выполняется условие Ляпунова (6.4) - все фазовые траектории направлены от состояния равновесия. Такое состояние равновесия называется «неустойчивый фокус» (неустойчивое состояние равновесия).

Рисунок 6.2 - Состояние равновесия типа «неустойчивый фокус»
Пусть  , тогда корни уравнения (7.8) будут вещественными отрицательными, т.е.
, тогда корни уравнения (7.8) будут вещественными отрицательными, т.е.  ,
,  . Фазовые траектории, характерные для таких корней представлены на рисунке 6.3. Выполняются условия Ляпунова (6.4) и (6.5) - все фазовые траектории сходятся к состоянию равновесия. Такое состояние равновесия называется «устойчивый узел» (асимптотически устойчивое состояние равновесия).
. Фазовые траектории, характерные для таких корней представлены на рисунке 6.3. Выполняются условия Ляпунова (6.4) и (6.5) - все фазовые траектории сходятся к состоянию равновесия. Такое состояние равновесия называется «устойчивый узел» (асимптотически устойчивое состояние равновесия).

Рисунок 6.3 - Состояние равновесия типа «устойчивый узел»
Пусть  , тогда корни уравнения (6.8) будут вещественными положительными, т.е.
, тогда корни уравнения (6.8) будут вещественными положительными, т.е.  ,
,  . Фазовые траектории, характерные для таких корней, представлены на рисунке 6.4. Не выполняется условие Ляпунова (6.4) - все фазовые траектории направлены от состояния равновесия. Такое состояние равновесия называется «неустойчивый узел» (неустойчивое состояние равновесия).
. Фазовые траектории, характерные для таких корней, представлены на рисунке 6.4. Не выполняется условие Ляпунова (6.4) - все фазовые траектории направлены от состояния равновесия. Такое состояние равновесия называется «неустойчивый узел» (неустойчивое состояние равновесия).
Пусть  , тогда корни уравнения (6.8) будут вещественными разными (один – положительный, другой – отрицательный), т.е.
, тогда корни уравнения (6.8) будут вещественными разными (один – положительный, другой – отрицательный), т.е.  ,
,  . Фазовые траектории, характерные для таких корней, представлены на рисунке 6.5. Не выполняется условие Ляпунова (6.4) - все фазовые траектории в конечном итоге направлены от состояния равновесия. Такое состояние равновесия имеет название «седло» (неустойчивое состояние равновесия).
. Фазовые траектории, характерные для таких корней, представлены на рисунке 6.5. Не выполняется условие Ляпунова (6.4) - все фазовые траектории в конечном итоге направлены от состояния равновесия. Такое состояние равновесия имеет название «седло» (неустойчивое состояние равновесия).

Рисунок 6.4 - Состояние равновесия типа «неустойчивый узел»

Рисунок 6.5 - Состояние равновесия типа «седло»
Пусть 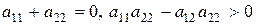 , тогда корни уравнения (6.8) будут комплексно-сопряженными с нулевой вещественной частью, т.е.
, тогда корни уравнения (6.8) будут комплексно-сопряженными с нулевой вещественной частью, т.е.  . Фазовые траектории, характерные для таких корней, представлены на рисунке 6.6. Выполняется условие Ляпунова (6.4) и не выполняется условие (6.5) – движения по фазовым траекториям осуществляются вокруг состояния равновесия (не приближаясь и не удаляясь). Такое состояние равновесия называется «центр» (устойчивое по Ляпунову состояние равновесия).
. Фазовые траектории, характерные для таких корней, представлены на рисунке 6.6. Выполняется условие Ляпунова (6.4) и не выполняется условие (6.5) – движения по фазовым траекториям осуществляются вокруг состояния равновесия (не приближаясь и не удаляясь). Такое состояние равновесия называется «центр» (устойчивое по Ляпунову состояние равновесия).

Рисунок 6.6 - Состояние равновесия типа «центр»
|
из
5.00
|
Обсуждение в статье: Геометрическая интерпретация устойчивости по Ляпунову |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

