 |
Главная |
Геометрическая интерпретация второго (прямого) метода Ляпунова
|
из
5.00
|
Движения системы второго порядка происходят в двухмерном пространстве переменных состояния - поверхности (частным случаем поверхности может быть плоскость). Движения системы третьего порядка происходят в трехмерном пространстве, четвертого – в четырехмерном и т.д. Поясним метод на примере динамической системы второго порядка (6.6), пространством состояний которой является плоскость переменных  .
.
Возьмем простейшую знакоопределенную функцию вида
 . (6.9)
. (6.9)
Пусть  , будем задавать постоянные значения функции, например
, будем задавать постоянные значения функции, например  ,
,  ,
,  и т.д. На плоскости состояний
и т.д. На плоскости состояний  функция
функция 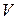 будет выглядеть в виде семейства окружностей, охватывающих состояние равновесия и обращаться в ноль в начале координат (представлено на рисунке 6.7).
будет выглядеть в виде семейства окружностей, охватывающих состояние равновесия и обращаться в ноль в начале координат (представлено на рисунке 6.7).
Пусть  , будем задавать постоянные значения функции
, будем задавать постоянные значения функции 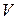 - на плоскости состояний функция будет выглядеть в виде семейства эллипсов, охватывающих состояние равновесия и также обращаться в ноль в начале координат
- на плоскости состояний функция будет выглядеть в виде семейства эллипсов, охватывающих состояние равновесия и также обращаться в ноль в начале координат  . Оси эллипса совпадают с координатами
. Оси эллипса совпадают с координатами  . При
. При  эллипс вытянут вдоль оси
эллипс вытянут вдоль оси  (представлено на рисунке 6.8), при
(представлено на рисунке 6.8), при  - вдоль оси
- вдоль оси  (представлено на рисунке 6.9).
(представлено на рисунке 6.9).
Возьмем еще одно уравнение функции
 . (6.10)
. (6.10)
Задаваясь различными (положительными) значениями функции 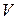 получим опять семейство эллипсов, оси которых в зависимости от численных значений коэффициентов
получим опять семейство эллипсов, оси которых в зависимости от численных значений коэффициентов  уже могут не совпадать с осями
уже могут не совпадать с осями  (представлено на рисунке 6.10).
(представлено на рисунке 6.10).
Согласно определению Ляпунова об устойчивости состояния равновесия, состояние равновесия асимптотически устойчиво, если все фазовые траектории (все движения в пространстве состояний) притягиваются этим состоянием равновесия (все траектории стремятся к состоянию равновесия); состояние равновесия неустойчиво, если все фазовые траектории (все движения в пространстве состояний) направлены от этого состояния равновесия в бесконечность. Состояние равновесия считается устойчивым по Ляпунову, если движения не уходят в бесконечность, но и не притягиваются состоянием равновесия, а все время находятся в некоторой окрестности состояния равновесия.
Представим, что мы не знаем, как выглядят фазовые траектории, т.е. мы не знаем притягиваются ли они состоянием равновесия или отталкиваются. Можно ли по исходным уравнениям динамики определить устойчивость (неустойчивость) состояния равновесия? Можно, если удастся найти функцию Ляпунова.
Примечание. До сих пор не существует общих методов отыскания функции Ляпунова. Поиском методов нахождения функции Ляпунова занимались многие ученые: В.И.Зубов (Ленинград), Е.А.Барбашин (Москва), А.И.Лурье (Москва), И.Г.Малкин (Москва), С.Левшец и Ж.Ла-Салль (США) и др.

Рисунок 6.7 – Функция 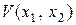 не является функцией Ляпунова
не является функцией Ляпунова

Рисунок 6.8 – Функция 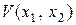 является функцией Ляпунова
является функцией Ляпунова
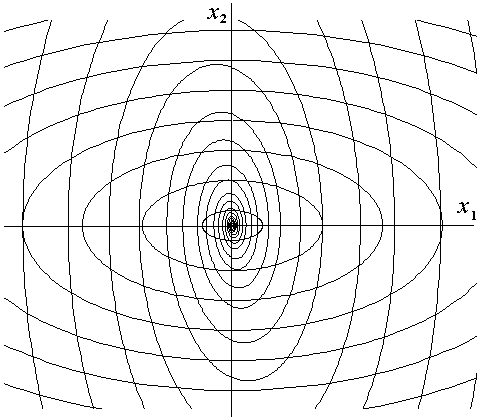
Рисунок 6.9 - Функция 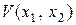 не является функцией Ляпунова
не является функцией Ляпунова

Рисунок 6.10 - Функция 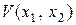 является функцией Ляпунова
является функцией Ляпунова
Поскольку координаты плоскости состояний  являются функциями времени, полная производная сложной функции
являются функциями времени, полная производная сложной функции 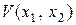 будет выглядеть как
будет выглядеть как
 . (6.11)
. (6.11)
Выясним смысл выражения (6.11). Обратим внимание, что с увеличением значений координат  значение функции
значение функции  возрастает. Определим вектор-градиент возрастания функции
возрастает. Определим вектор-градиент возрастания функции  как:
как:
 , (6.12)
, (6.12)
где  - единичные векторы – орты координат.
- единичные векторы – орты координат.
Рассмотрим плоскость  в смысле плоскости состояний системы. Во время движения системы ее координаты
в смысле плоскости состояний системы. Во время движения системы ее координаты  изменяются, принимая в каждый момент времени определенные значения. Если координаты представить в виде точки (такая точка называется изображающей), то перемещение этой точки во времени и составит фазовую траекторию. Мгновенная скорость перемещения изображающей точки по фазовой траектории определяется выражением
изменяются, принимая в каждый момент времени определенные значения. Если координаты представить в виде точки (такая точка называется изображающей), то перемещение этой точки во времени и составит фазовую траекторию. Мгновенная скорость перемещения изображающей точки по фазовой траектории определяется выражением
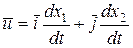 . (6.13)
. (6.13)
Возьмем скалярное произведение вектора (6.12) и вектора (6.13)
 . (6.14)
. (6.14)
Итак, геометрический смысл  - скалярное произведение двух векторов (6.14), один вектор показывает направление возрастания функции
- скалярное произведение двух векторов (6.14), один вектор показывает направление возрастания функции  , другой – мгновенную скорость перемещения изображающей точки на плоскости.
, другой – мгновенную скорость перемещения изображающей точки на плоскости.
Если угол между векторами тупой (  ), то
), то  и соответственно
и соответственно  . С геометрической точки зрения это означает, что все фазовые траектории пересекают поверхности уровня функции в сторону ее уменьшения - в сторону состояния равновесия (представлено на рисунке 6.11).
. С геометрической точки зрения это означает, что все фазовые траектории пересекают поверхности уровня функции в сторону ее уменьшения - в сторону состояния равновесия (представлено на рисунке 6.11).
Если угол между векторами острый (  ), то
), то  и соответственно
и соответственно  . С геометрической точки зрения это означает, что все фазовые траектории пересекают поверхности уровня функции в сторону ее увеличения - от состояния равновесия (представлено на рисунке 6.12).
. С геометрической точки зрения это означает, что все фазовые траектории пересекают поверхности уровня функции в сторону ее увеличения - от состояния равновесия (представлено на рисунке 6.12).

Рисунок 6.11 – Геометрическая интерпретация метода ( 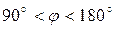 )
)
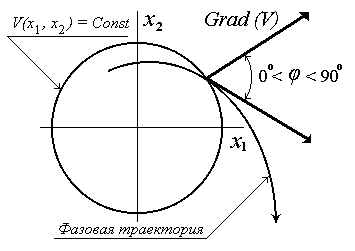
Рисунок 6.12 - Геометрическая интерпретация метода (  )
)
Рассмотрим пример 1. Пусть уравнения возмущенного движения имеют вид
 (6.15)
(6.15)
Требуется определить устойчивость (неустойчивость) состояния равновесия
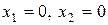 . (6.16)
. (6.16)
Применим первый метод Ляпунова – определение устойчивости состояний равновесия (6.16) для нелинейных уравнений возмущенного движения (6.15) по соответствующей линейной модели (соответствующим линейным уравнениям возмущенного движения). Необходимо линеаризовать уравнения (6.15), для этого будем считать, что переменные 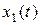 ,
,  всегда находятся вблизи состояния равновесия (переменные
всегда находятся вблизи состояния равновесия (переменные 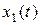 и
и  достаточно малы). Тогда произведение переменных будет малой величиной более высокого порядка. Пренебрежение малыми величинами более высокого порядка в уравнениях (6.15) позволяет получить соответствующую линейную модель.
достаточно малы). Тогда произведение переменных будет малой величиной более высокого порядка. Пренебрежение малыми величинами более высокого порядка в уравнениях (6.15) позволяет получить соответствующую линейную модель.
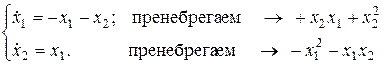 (6.17)
(6.17)
Характеристическое уравнение системы (7.17) имеет вид
 . (6.18)
. (6.18)
Корни уравнения (6.18)  - комплексно-сопряженные с отрицательной вещественной частью. Состояние равновесия устойчиво, тип состояния равновесия «устойчивый фокус».
- комплексно-сопряженные с отрицательной вещественной частью. Состояние равновесия устойчиво, тип состояния равновесия «устойчивый фокус».
Рассмотрим пример 2. Уравнения возмущенного движения имеют вид
 (6.19)
(6.19)
Как и в предыдущем примере требуется определить устойчивость (неустойчивость) состояния равновесия  . Рассмотрим соответствующую линейную модель уравнений (6.19)
. Рассмотрим соответствующую линейную модель уравнений (6.19)
 (6.20)
(6.20)
Характеристическое уравнение (7.20) имеет вид 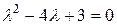 , корни которого
, корни которого  - вещественные положительные. Состояние равновесия неустойчиво, тип состояния равновесия «неустойчивый узел».
- вещественные положительные. Состояние равновесия неустойчиво, тип состояния равновесия «неустойчивый узел».
Рассмотрим пример 3. Уравнения возмущенного движения следующие
 (6.21)
(6.21)
Соответствующая линейная модель имеет вид
 (6.22)
(6.22)
Корни характеристического уравнения  чисто мнимые (комплексно-сопряженные с нулевой вещественной частью). Определить устойчивость (неустойчивость) состояния равновесия с помощью первого метода не предоставляется возможным, состояние равновесия может оказаться как устойчивым, так и неустойчивым.
чисто мнимые (комплексно-сопряженные с нулевой вещественной частью). Определить устойчивость (неустойчивость) состояния равновесия с помощью первого метода не предоставляется возможным, состояние равновесия может оказаться как устойчивым, так и неустойчивым.
Применим второй метод Ляпунова. Возьмем положительную знакоопределенную функцию вида
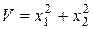 . (6.23)
. (6.23)
Если производная  окажется знакоопределенной функцией противоположного с
окажется знакоопределенной функцией противоположного с  знака, т.е.
знака, т.е.  , то состояние равновесия устойчиво асимптотически, если
, то состояние равновесия устойчиво асимптотически, если  - устойчиво по Ляпунову, если одного с
- устойчиво по Ляпунову, если одного с  знака, т.е.
знака, т.е.  - неустойчиво.
- неустойчиво.
Вычислим полную производную сложной функции  , а именно:
, а именно: 
После приведения подобных слагаемых получим
 . (6.24)
. (6.24)
Функция (6.24) не является ни знакоопределенной ни знакопостоянной. Следовательно, нам не удалось подобрать функцию Ляпунова.
Возьмем другую положительную знакоопределенную функцию вида
 . (6.25)
. (6.25)
Вычислим производную 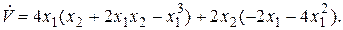 После раскрытия скобок и приведения подобных слагаемых получим
После раскрытия скобок и приведения подобных слагаемых получим
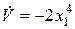 . (6.26)
. (6.26)
Функция (6.26) является знакоопределенной функцией противоположного с функцией (6.25) знака. Нам удалось подобрать функцию Ляпунова (функция (6.25)) и доказать асимптотическую устойчивость состояния равновесия системы (6.21). В каждой точке плоскости (за исключением точки состояния равновесия) характер пересечения линий уровня функции Ляпунова (6.25) и фазовых траекторий, получаемых при интегрировании уравнений (6.21), соответствует геометрическому образу, представленному на рисунке 6.11.
На рисунках 6.7, 6.9 геометрически представлены случаи неудачного подбора знакоопределенной функции, на рисунках 6.8, 6.10 – удачного (знакопределенная функция является функцией Ляпунова).
Рисунок 6.11 демонстрирует, насколько может быть труден подбор функции Ляпунова в случае состояния равновесия типа «седло».

Рисунок 6.11 – Состояние равновесия типа «седло». Подбор функции Ляпунова
|
из
5.00
|
Обсуждение в статье: Геометрическая интерпретация второго (прямого) метода Ляпунова |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

