Шаг второй. Дидактическая схема.

Как мы уже указывали, выбор предметного материала продиктован, в первую очередь, стремлением предложить школьникам разобраться в важной для современной науки и достаточно общей проблеме. Поэтому выбор предметного материала – это работа по поиску такой проблемы и анализу соответствующих исследований с тем, чтобы эту проблему сформулировать.

Современная наука, и в первую очередь, физика создали за многие годы своего становления и развития очень мощный понятийный аппарат и огромное множества более или менее общих моделей, которые позволяют описывать поведение одиночных, изолированных объектов. Собственно, вычленение объекта из его окружения, изоляция его свойств и структуры от тех условий, в которые он помещен, является необходимым условием его успешного модельного описания в рамках физики.

В химии дело обстоит несколько сложнее. С одной стороны, химия возникала как препаративная область практики, связанная с синтезом новых соединений и исследованием их свойств путем проведения химических реакций. В этом направлении был достигнут огромный успех – современная химия синтезирует до миллиона новых соединений в год. Но каждый химик, знакомый с методиками осуществления синтезов знает, какое важное значение играют при этом внешние условия.

С другой стороны, развитие химии как теоретической науки связано, прежде всего, с привлечением физических онтологий. Химическая термодинамика, химическая кинетика, квантовая химия – все эти дисциплины созданы путем использования по отношению к объектам химии – веществам и реакциям – физических моделей. Именно поэтому теоретическое описание этих объектов может строиться только тогда, когда они вычленены из окружающих условий. Это особенно верно по отношению к квантовой химии, которая, между тем, предпринимает попытки объяснить устройство всех химических объектов.

Получается, что как только дело доходит до описания и исследования коллективного поведения огромного множества объектов, как это происходит каждый раз, когда мы сталкиваемся с химической реакцией или просто с веществом, мы такого описания построить не можем.

Единственное исключение составляют те коллективные явления, которые адекватно схватываются моделью идеального газа – такой же монопроцессуальной моделью, как и все модели в физике. Невозможность увидеть на одном и том же объекте развертывание двух и более соотносящихся друг с другом процессов – это и есть ключевая, на наш взгляд, проблемная точка современной науки.

Наиболее же самобытная теория химического строения вещества – теория Бутлерова, при всей своей силе является, как мы показывали также в описании курса «Развитие химических представлений о веществе», теорией структурной. Она по своему категориальному устройству не способна видеть и описывать процессы.

Таким образом, речь идет о той проблеме, которая в науке получила название проблемы самоорганизации (или синергии по Хакену), или проблемы нелинейности коллективного поведения объектов, когда в принципе не может быть выделен и очерчен один ведущий процесс так, чтобы все остальные процессы могли бы быть учтены в виде поправок.

Это наблюдается, с одной стороны, в том, что рассматриваемый объект (который уже не есть просто совокупность отдельных объектов) приобретает собственное сложное поведение, приобретает меняющуюся структуру, самоорганизуется, самособирается из некоторых элементов и при этом демонстрирует аномальные с точки зрения имеющихся моделей свойства. С другой стороны, оказывается, что у нас практически не существует математического аппарата, который позволял бы количественно описывать такого рода явления. Дифференциальные уравнения и линейная алгебра – основа используемого в физике математического аппарата, не могут эффективно справляться с такими эффектами, в которых зависимость свойств кольцевая и, поэтому, нелинейная. В каком-то смысле само понятие функции работает только тогда, когда мы можем выделить аргумент и зависящую от него функцию. В том случае, если непонятно, что является аргументом, а что – функцией, обычная дифференциальная математика искомых решений дать не может.

Итак, мы выделили проблему, или область нашего незнания, неприменимости наших моделей. Это все случаи, когда мы наблюдаем такое коллективное поведение двух и более объектов, которые включены в более чем один процесс, а сами процессы при этом взаимосвязаны.

Типичным случаем, когда при исследовании выявляется сложное коллективное поведение, является исследование химико-физических свойств воды. Это вещество демонстрирует богатый набор аномальных свойств, а также очень сложное, постоянно изменяющееся внутреннее строение. При этом аномалии свойств воды просто понятны, и эти свойства не могут быть описаны ни теми моделями, которые есть у школьников, хорошо знающих предмет физики, ни теми, которые есть у современной науки. Поэтому мы выбрали в качестве основного объекта для моделирования именно воду.

Другим частым случаем столкновения с самоорганизацией является исследование взаимных колебаний двух микро- или макроскопических объектов. В этой области обнаруживается богатый набор необъяснимых эффектов нелинейного характера. При этом в силу своей наглядности, такие – маятниковые – объекты более удобны для работы со школьниками. Поэтому мы выбрали именно работу по моделированию аномальных колебаний маятников в качестве той точки, где моделирование должно было вывести нас к новому знанию. Тому знанию, которое позволило бы приблизиться к описанию многих процессов, завязанных на одном и том же материале.

В целом структура курса представлена тремя большими тематическими и функциональными блоками. Каждый из блоков организован в соответствии с указанными нами принципами. При этом в рамках каждого блока проходит несколько циклов моделирования, но моделируемые объекты все время меняются.

Первый блок посвящен выделению аномальных свойств воды и восстановлению таких предметных моделей, которые должны описывать данное поведение воды, но не могут этого сделать. Таким образом, первый блок посвящен восстановлению имеющихся в науке моделей: модели теплоемкости идеального газа и идеального кристалла, а также модели водородных связей в воде. Первый блок завершается фиксацией тех экспериментальных данных, которые не могут быть объяснены этими моделями, и очерчиванием круга подходов к решению данной проблемы.

На втором блоке происходит резкая смена предметного материала. Здесь осуществляется моделирование маятниковых объектов. Целью второго блока является выделение нового физического принципа взаимодействия. Для этого проводится моделирование физического маятника (практически, восстановление имеющейся предметной модели), восстановление стоящих за моделью идеализаций и понятий. После этого данные идеализации безуспешно применяются при моделировании нелинейного арументного маятника. Построение модели такого маятника позволяет рефлексивно и аналитически вычленить новый физический принцип.

Наконец, третий блок предполагает ситуацию применения нового физического принципа и его расширение при моделировании устройства воды. Так происходит возвращение к первоначально заявленной физической проблеме, но с расширением используемого материала. Всего за курс происходит порядка 10 циклов моделирования.

Мы сосредоточим свое внимание только на втором блоке, посвященном моделированию маятников и колебаний. При этом мы сосредоточим особое внимание на том, как разнообразно осуществлялось моделирование, какие процессы метапредметной работы и как при помощи моделирования запускались, а также на том, как происходило последовательное движение в получении нового знания о том, как могут быть описаны процессы. Но до описания самого курса нам необходимо обсудить принципиальное устройство такой деятельности, как моделирование, и соответственно, дидактическую схему всего курса в целом, которой и выступает схема моделирования.

Схема моделирования (Схема 24) достаточно проста по всему устройству, но эта простота предоставляет очень богатые возможности для движения по этой схеме с получением как богатого набора побочных результатов, так и с построением целевого продукта этой деятельности – работоспособных моделей.

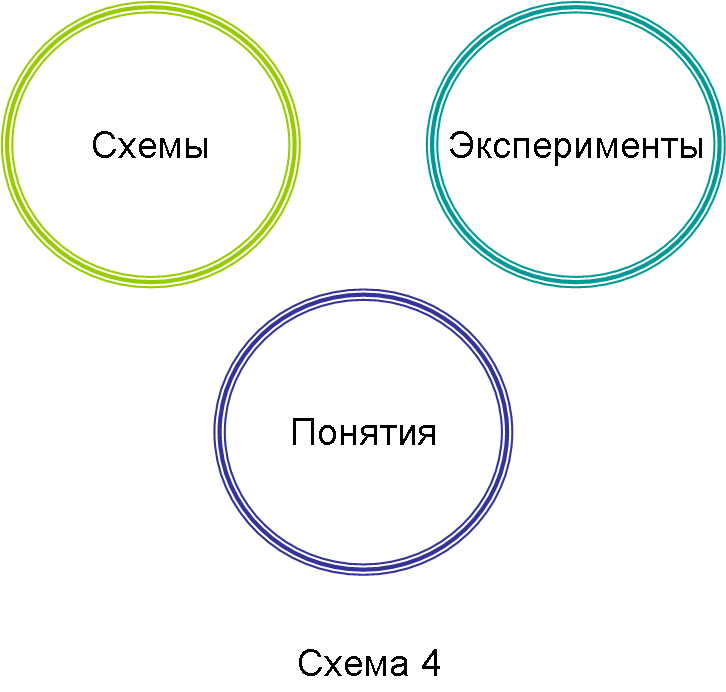
Схема 24

С одной стороны, модель является схемой. Она должна схватывать идеальное содержание нашего видения объекта. Причем модель является синтетической схемой – она собирается из определенного набора базовых идеализаций, закрепленных в конструктивах на схеме, но кроме того, она предполагает четко определенные правила сборки этих конструктивов и, соответственно, идеализаций в единую картинку. В рамках этой картинки конструктивы должны «жить» сообразно законам существования данной модели (Схема 25).

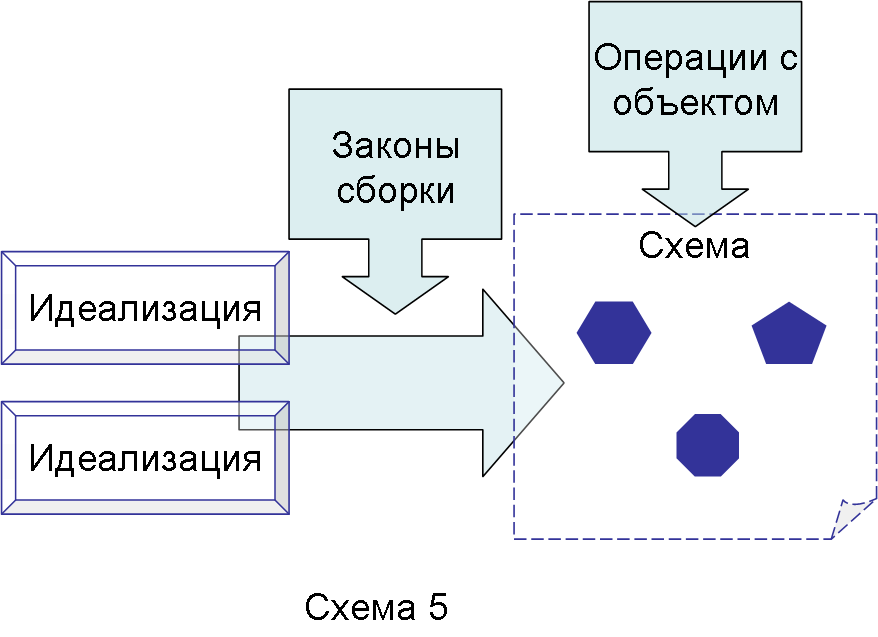
Схема 25

Выстраивая модель, мы не просто набираем элементы этой модели и определяем каждому элементу свое функциональное место, но и задаем такое описание, которое говорит о том, что начинает происходить с элементами, когда модель верно из них собрана. В каком-то смысле, знаковый, схемный, или семиотический фокус модели представляет из себя сборочный чертеж. Но это – только чертеж, а сама модель обязательно включает в себя некоторое внутреннее происходящее.

При этом принципы сборки и разборки моделей, также как и возможные или невозможные в ней события определяются теми категориями, которые мы используем в нашем мышлении. Модель всегда адекватна только данным категориям, а потому допускает только те или иные действия с собой.

На самом деле, то происходящее с элементами, что фиксируется моделью, является нашими действиями с моделируемым объектом. Так, если в модели водородных связей ключевым является правило разрыва и образования этих связей, это фиксирует только тот момент, что в нашем оперировании со связями мы установили, что с ними возможно производить те, а не иные действия. Впрочем, далее в рамках натурального подхода осуществляется достаточно сложное, но ключевое полагание. Получив правила осуществления действий с объектом, мы говорим, что эти действия сообразны не нашему оперированию с ним, а естественно происходящему внутри него. Тогда мы можем прописывать правила внутренней жизни элементов модели, говоря, что эти правила – суть законы существования объекта, а сам объект, его устройство и его существование фиксируются моделью.

Вокруг этого вопроса – правомерно ли приписывать действительному устройству объекта те особенности, которые отличают наши с ним операции, – развернулась одна из наиболее острых дискуссий в естественных науках XX века. Речь идет о знаменитых Сольвеевских конгрессах и непримиримом споре между Эйнштейном и Бором. Все дело в том, что авторы копенгагеновской интерпретации квантовой механики, получая только вероятностные результаты в своих измерениях свойств микрообъектов, эту вероятностную природу приписали самим микрообъектам.

Как мы уже упомянули, операции, производимые с моделью и ее элементами, диктуются используемыми категориями. Но кроме категорий они задаются также используемыми предметными понятиями. Собственно, категории «вшиты» в структуру этих используемых понятий. Мы всегда строим модель, опираясь на наши знания. В этом плане мы можем построить только такую модель, которая собирается на основе имеющихся у нас понятий. Здесь показателен знаменитый случай, описываемый Миклухо-Маклаем: аборигены Папуа-Новой Гвинеи, впервые увидев зеркало, назвали его «твердой водой», поскольку они использовали только доступные им понятийные точки.

Таким образом, из эпистемического фокуса модель является набором используемых при ее построении понятий. Эти понятия служат своего рода цветными стеклами, позволяющими увидеть моделируемый объект в преломленном и окрашенном этими понятиями виде. Модель всегда показывает нам схватываемый ею объект через призму используемых понятий.

 Наконец, последний, третий фокус существования модели – это эксперимент. Модель должна строиться адекватно объекту, а значит – опираться на результаты наших операций с этим объектом. Если модель оказывается неадекватна полученным экспериментальным данным, она оказывается неработоспособной. Экспериментальные данные как раз дают нам сведения о тех операциях, которые сообразны устройству объекта и о тех операциях, которые не сообразны. На основе этих данных создаются правила «внутренней жизни» элементов модели.

Мы описали пока что только некоторые топы в моделировании – схемы, понятия, эксперименты. Важнейшим является вопрос взаимной функционализации этих топов, их взаимосвязи и возможных типов движения по ним. Как мы упомянули, схема моделирования предполагает возможность реализации большого набора вариантов такого движения. Здесь все зависит от задачи. Если перед нами стоит задача проверки адекватности имеющихся понятий, мы на основе этих понятий создаем такую схему, которая выступала бы схемой результатов, полученных в еще не состоявшемся эксперименте. Если результаты, которые мы получаем в реальном эксперименте, соответствуют схеме, то понятия оказываются верными, адекватными.

 Если перед нами стоит задача исследования какого-то объекта, мы строим на основе имеющихся понятий такую схему, которая выступала бы схемой эксперимента: необходимые операции с объектом и точки получения экспериментальных данных. Такие циклы, каждый из которых имеет свою начальную точку и свою логику разворачивания, может, вообще говоря, много.

Нас в данном случае интересуют только некоторые из разворачиваний цикла моделирования. Во-первых, речь идет о таком моделировании, которое позволяет восстанавливать за моделями идеализации и понятия. Во-вторых, нас интересует такое моделирование, которое позволяет сталкивать имеющиеся понятия и построенные на их основе схемы с экспериментальными данными и тем самым показывать границы их возможностей, а значит – очерчивать границы незнания.

Но самый большой интерес вызывает такое моделирование, в котором на основе анализа проводимого эксперимента производится схематизация феноменально обнаруженного нового эффекта. После этого разрабатываются такие новые идеализации и вообще знания, которые позволили бы перейти от схемы, фиксирующей эффект, к схеме, его объясняющей. Это движение позволяет делать моделирование технологией получения новых знаний и их деятельностной проверки. Как видно, именно наличие понятийного фокуса делает моделирование эпистемической технологией.

Между тем, идеализационная работа не заложена в схему моделирования. Здесь мы осуществляем неизбежный выход из этой схемы в действительность метапредмета «Знание», и должны использовать эпистемическую технологию идеализации (Схема 26).

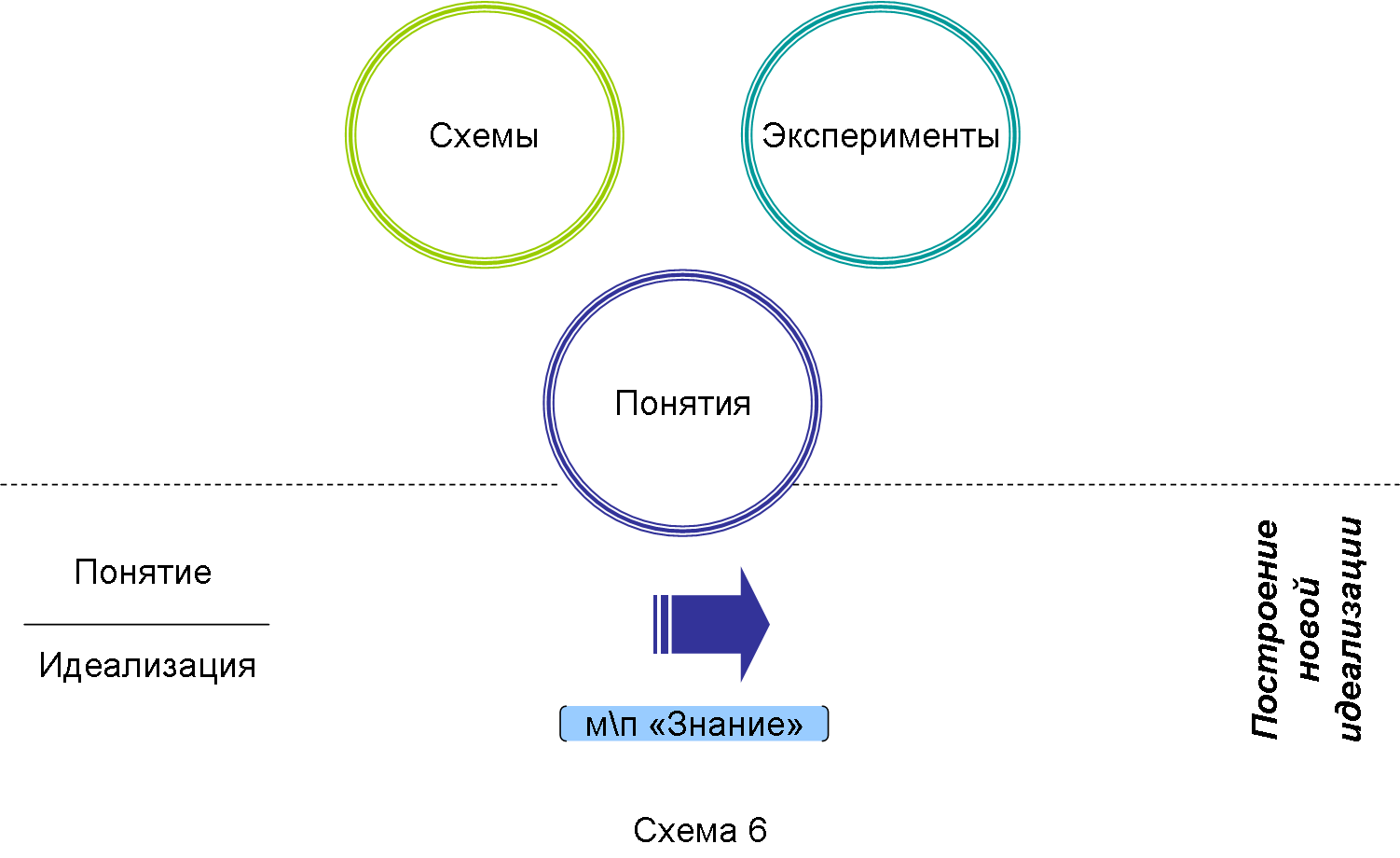
Схема 26

Такое идеализационной движение осуществляется, как правило, путем смысловой прочистки построенных при моделировании схем и свободном предложении нового идеального видения объекта или элемента модели. Предложение новой идеализации, идеального принципа или видения задает возможность для появления новой сборки схемы или новых конструктивов. Поскольку новые идеализации возникают, в каком-то смысле, как некоторое прозрение, когда мы видим невидимый идеальный объект, причем по-новому, так важно при идеализационной работе способность воображения.

«Идеализация – это идеальный конструкт, или идеальный теоретический объект, лежащий в основе того или другого предметного понятия и определяющий его смысл, а если рассматривать шире – то в основе той или другой предметной области»[5], - пишет в учебнике по метапредмету «Знание» Н.В. Громыко. В своей работе мы старались как раз задавать рамку выделения наиболее базовых для того или иного подхода к физике идеализаций.

При этом основной была работа по построению новой идеализации, а значит – нового знания, которое позволило бы школьникам модельно описывать результаты уникальных экспериментов. Это была та точка, в которой схема моделирования позволяет выводить школьников к новому научному знанию.

Совершенно особенным типом движения по схеме моделирования является движение, призванное обеспечить смену используемого нами типа схем. Это моделирование предполагает нахождение такого схематического языка и таких подходов к схематизации, при которых оказалось бы возможным схватить в схеме как предметные операции, адекватные обнаруженным в эксперименте эффектам, так и используемые при моделировании понятия. Устройство используемых схем определяет нашу возможность увидеть, или же наоборот, невозможность видеть, какие-то важнейшие аспекты устройства объекта. Без соответствующих схем невозможно применение новых идеализаций. Только соответствие всех трех топов задает момент наличия модели и ее работоспособности.

Развитие возможностей схематизации в науке, на наш взгляд, связано со сменой используемых категорий. Ю.В. Громыко пишет: «За категориями и категориальными мирами стоят целые формации мышления и мыследеятельности. И часто категориальные оппозиции, задаваемые одной парой, снимаются, выводятся из употребления при введении новой категории. Те противоречия, которые были неразрешимы при действии одной категориальной пары, становятся вполне разрешимы при введении новой»[6]. Поскольку именно категории, заложенные в устройство схем, определяют наше движение по этим схемам, категориальный анализ позволяет осуществлять разработку новых типов схем и попытки смены категорий собственного мышления. При этом важно отметить, что в данной области нашей работы мы опять же выходим за рамки схемы моделирования. Здесь происходит зацепление содержания метапредмета «Знак», а именно категориального анализа схем (Схема 27).

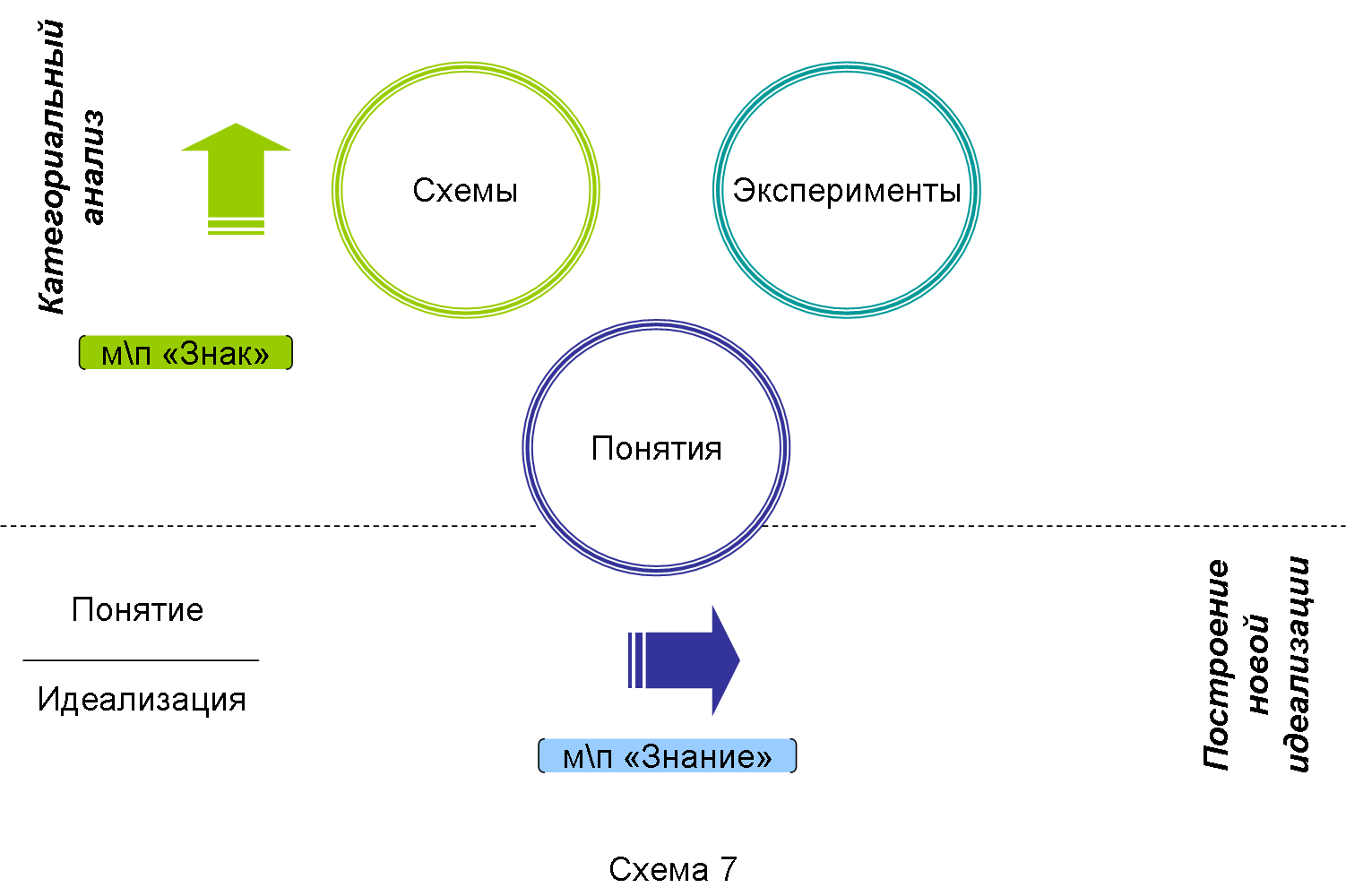
Схема 27

Какую же смену категорий мы программируем, закладываем в устройство курса? Одна из этих категорий нами уже упоминалась при анализе выбранной для работы научной проблемы. Это – категория процесса. С одной стороны, сам ход от категории структуры и структурных схем, о которых мы писали в статье про курс «Развитие химических представлений об устройстве вещества», является делом непростым. Но уход в действительность физики позволяет начать оперировать с процессами и видеть их, поскольку процессуальное мышление – центральное в физике. Конечно, мы не сможем мыслить процессуально химические объекты, в том числе, потому что, видимо, категория процесса является слабой для химической действительности. Но сама возможность строить процессуальные модели у нас появляется с ходом в физику. Что же значит, мыслить нечто как процесс? Г.П. Щедровицкий описывал, что «если мы можем получать последовательно некоторые специфические модели какого-то объекта м₁, м₂, м₃ и т.д. через некоторые промежутки времени и можем эти модели прикладывать друг к другу и или вкладывать друг в друга, например, как с отрезками пути, разбивая м₂ на м₁ и Δм, то таким образом собранное изображение объекта мы называем процессуальным изображением...»[7].

Поэтому такую роль в физике играют математические функции. Они позволяют фиксировать связанные изменения числовых характеристик моделей объекта, задают математическое описание сборки отдельных представлений объекта в единое процессуальное представление.

Как мы отмечали, категория процесса задает на настоящий момент границу физического и наиболее передового химического мышления. Она не позволяет видеть такие объекты, в которых сосуществуют и взаимно определяют друг друга множество процессов, в которые в каждый момент по-своему включены различные взаимосвязанные объекты. Категория, которая способна видеть такого рода объекты, – это категория системы. Поэтому из фокуса развития категориального аппарата учащихся, мы обучаем их системному подходу и системному мышлению. Системный подход очень подробно разрабатывается в трудах замечательного русского философа и методолога Г.П. Щедровицкого. Он пишет: «Суть нового подхода можно выразить в весьма простом принципе: рассмотреть какой-либо объект в виде сложной системы — значит представить его последовательно в четырех категориальных планах — процессов какого-то одного вида, функциональной структуры, организованностей материала, морфологии...»[8].

И далее: «Другое преимущество состоит в том, что без затруднений и парадоксов решается проблема взаимодействия систем...»[9]. Этот момент – то, что категория системы позволяет видеть и описывать взаимодействия, является для нас центральным. Дело обстоит таким образом, что именно представление о взаимодействии, а не о воздействии дает возможность моделировать самоорганизующиеся процессы, и, что самое важное, не видеть их как отклонение от нормы законосообразного поведения природных объектов.

Таким образом, в рамках описываемого фрагмента курса, который является самым важным в плане эпистемической работы, мы должны были осуществить смену используемой категории с оппозиции структура – процесс на категорию системы и в соответствии с этим построить идеализацию взаимодействия – новый физический принцип (Схема 28).

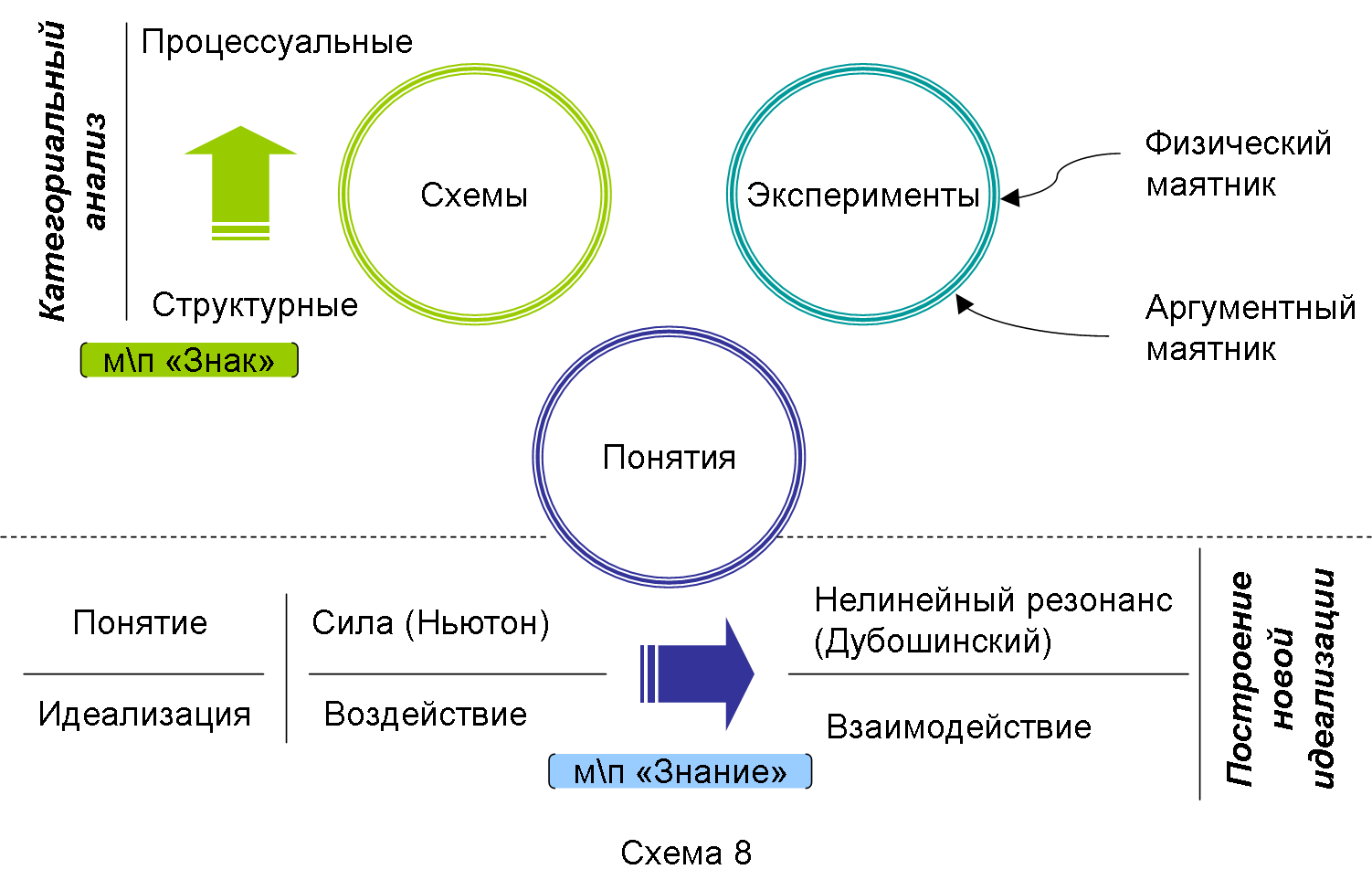
Схема 28

При этом мы осуществляли два цикла моделирования и строили сначала модель физического маятника, потом – модель аргументного маятника. Далее мы покажем, как строилась эта работа, опираясь на построенную дидактическую схему курса – схему моделирования.