Вычисление корней полинома.

ЛЕКЦИЯ 5

 

Элементы программирования в среде MATLAB

 

Операции над полиномами

В системе MATLAB имеется большое количество функций для работы с полиномами, с использованием которых можно вычислить значение полинома, найти корни полинома, выполнить операции умножения и деления полиномов, произвести дифференцирование и интегрирование полиномов.

Как известно, полином (или многочлен) – это выражение вида

,

где  – постоянные коэффициенты.

В MATLAB полином задается и хранится в виде вектора, элементами которого являются коэффициенты полинома

.

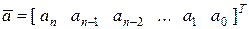Так, например, для задания полинома  следует ввести команду:

>> p=[5 -4 2 -1 8]

p =

5 -4 2 -1 8

 

Вычисление значения полинома.

Для вычисления значения полинома от некоторого аргумента предназначена функция polyval, имеющая следующий синтаксис:

y=polyval(p,x)

где p – вектор коэффициентов полинома; x – значение аргумента.

В частности, для рассматриваемого полинома можем вычислить

>> polyval(p,2)

ans =

62

В качестве аргумента может быть задан вектор или матрица. В этом случае значение полинома будет вычислено для каждого элемента данного вектора или матрицы, в результате чего будет сформирован вектор или матрица того же размера, что и аргумент x. Например:

>> p=[2 0 4 6];

>> x=[1 3; 2 7];

>> y=polyval(p,x)

y =

12 72

30 720

 

Пример выполнения лабораторной работы.

Пример 1. Табулирование полинома  на отрезке [ , 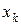] с последующим построением графика, а также выдачей максимального и минимального значения функции и точек, где эти значения достигаются,

, ,

 

Пример текста М-файла

p=input('ввести коэффициенты полинома: [a(n),a(n-1),...,a(1),a(0)]=');

xn=input('ввести начальное значение xn=');

xk=input('ввести конечное значение xk=');

n=input('ввести значение n=');

h=(xk-xn)/n;

x=xn:h:xk;

y=polyval(p,x);

[fmin,imin]=min(y);

[fmax,imax]=max(y);

fprintf('\n fmin=%8.2f в точке xmin=%6.2f \n fmax=%8.2f в точке xmax=%6.2f \n',fmin,x(imin),fmax,x(imax))

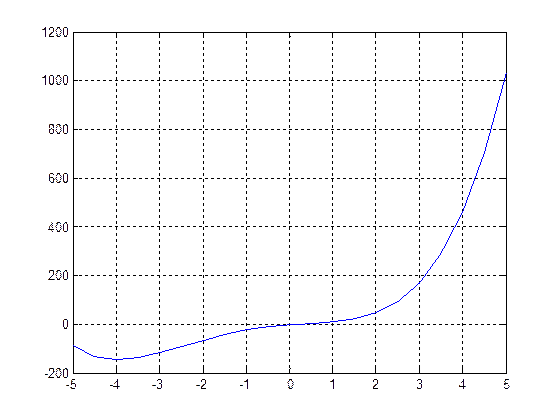
plot(x,y),grid on

 

Результаты счета

ввести коэффициенты полинома: [a(n),a(n-1),...,a(1),a(0)]=[1 4 -6 12 -1]

ввести начальное значение xn=-5

ввести конечное значение xk=5

ввести значение n=20

 

 fmin= -145.00 в точке xmin= -4.00

 fmax= 1034.00 в точке xmax= 5.00

 

Вычисление корней полинома.

Вычислить все корни полинома можно с помощью функции roots (причем число корней полинома всегда совпадает со степенью полинома).

Вычислив корни полинома, можно восстановить коэффициенты приведенного полинома (т.е. полинома, у которого коэффициент при старшей степени равен 1). Для этих целей в MATLAB имеет функция poly:

>> p=[2 -6 6 -6 4];

>> r=roots(p)

r =

2.0000 + 0.0000i

0.0000 + 1.0000i

0.0000 - 1.0000i

1.0000 + 0.0000i

>> p1=poly(r)

p1 =

1.0000 -3.0000 3.0000 -3.0000 2.0000

Для того, чтобы получить коэффициенты исходного полинома, следует умножить полученные вектор коэффициентов на коэффициент при старшей степени полинома (в рассматриваемом примере он равен 2):

>> p1*2

ans =

2.0000 -6.0000 6.0000 -6.0000 4.0000

 

Пример 2. Найти корни полинома ,

Пример текста М-файла

p=input('ввести коэффициенты полинома: [a(n),a(n-1),...,a(1),a(0)]=');

r=roots(p);

fprintf('\n корни полинома:\n'),disp(r)

 

Результаты счета

вести коэффициенты полинома: [a(n),a(n-1),...,a(1),a(0)]=[1 4 -6 12 -1]

корни полинома:

-5.4953         

0.7042 + 1.2643i

0.7042 - 1.2643i

0.0869         

>>