Дифференцирование и интегрирование полиномов.

Для нахождения производной от полинома можно использовать функцию polyder, к которой можно обратиться различными способами (в зависимости от необходимого результата):

q=polyder(p) – выполняется вычисление вектора коэффициентов полинома-производной (q) от исходного полинома, заданного вектором коэффициентов p;

c=polyder(a,b) – выполняется вычисление производной от произведения двух полиномов, заданных векторами коэффициентов a и b;

[q,d]=polyder(a,b) – выполняется вычисление производной от отношения двух полиномов, заданных векторами коэффициентов a и b, причем результат выдается в виде отношения полиномов q и d, т.е. q/d.

Пусть, например, требуется вычислить производную от уже рассматривавшегося выше полинома 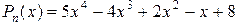. Имеем:

>> p=[5 -4 2 -1 8];

>> q=polyder(p)

q =

20 -12 4 -1

Вычислим теперь производную от произведения двух полиномов:

>> a=[1 2 9];

>> b=[-4 7];

>> c=polyder(a,b)

c =

-12 -2 -22

Заметим, что тот же результат можно получить, если предварительно перемножить полиномы с использованием функции conv, после чего определить производную от этого произведения:

>> p=conv(a,b)

p =

-4 -1 -22 63

>> c=polyder(p)

c =

-12 -2 -22

Для интегрирования полиномов служит функция polyint, имеющая следующий синтаксис:

q=polyint(p,k)

где k – константа (постоянная) интегрирования, которая может быть опущена (по умолчанию принимается равной нулю).

Приведем пример:

>> p=[2 5 7 -4];

>> q=polyint(p)

q =

0.5000 1.6667 3.5000 -4.0000    0

 

Пример 5. Табулирование полинома 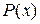, его производных и первообразной на отрезке [ 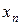, 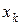] с последующим построением  графиков,

, ,

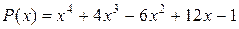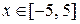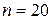
Пример текста М-файла

p4=input('ввести коэффициенты полинома: [a(n),a(n-1),...,a(1),a(0)]=');

p3=polyder(p4); % 1-я производная

p2=polyder(p3); % 2-я производная

p1=polyder(p2); % 3-я производная

p0=polyder(p1); % 4-я производная

p5=polyint(p4); % 1-я первообразная

xn=input('ввести начальное значение xn=');

xk=input('ввести конечное значение xk=');

n=input('ввести значение n=');

h=(xk-xn)/n;

x=xn:h:xk;

y0=polyval(p0,x);

y1=polyval(p1,x);

y2=polyval(p2,x);

y3=polyval(p3,x);

y4=polyval(p4,x);

y5=polyval(p5,x);

hold on

plot(x,y4,'r',x,y3,'b',x,y2,':b',x,y1,'c',x,y0,'m',x,y5,'g'),grid on

legend('P','dP','d2(P)','d3(P)','d4(P)','int(P)',0)

 

Результаты счета

ввести коэффициенты полинома: [a(n),a(n-1),...,a(1),a(0)]=[1 4 -6 12 -1]

ввести начальное значение xn=-5

ввести конечное значение xk=5

ввести значение n=20

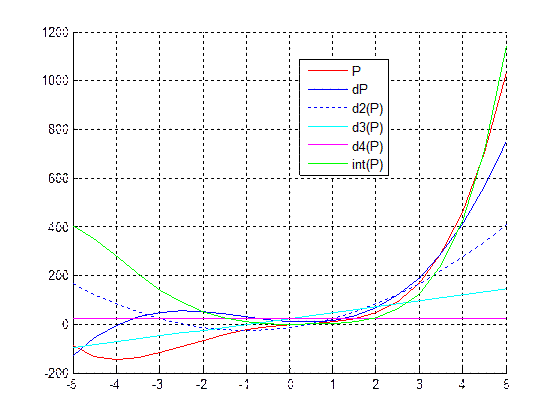
Пример 6. Табулирование полинома 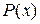, , 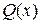производной от :

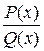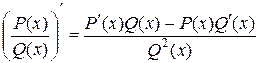
на отрезке [ 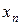, 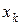] с последующим построением  графиков, где

, ,

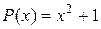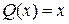т.е. 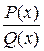 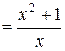                               и ,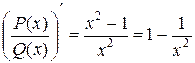

,

 

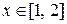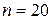
Пример текста М-файла

p=input('ввести коэффициенты полинома P : [a(n),a(n-1),...,a(1),a(0)]=');

q=input('ввести коэффициенты полинома Q: [a(n),a(n-1),...,a(1),a(0)]=');

[t r]=polyder(p,q) % производная P/Q

[tr rr]=deconv(t,r) % tr-коэффициенты полинома TR частного и остатка RR от деления T/R

xn=input('ввести начальное значение xn=');

xk=input('ввести конечное значение xk=');

n=input('ввести значение n=');

h=(xk-xn)/n;

x=xn:h:xk;

P=polyval(p,x);

Q=polyval(q,x);

T=polyval(t,x);

R=polyval(r,x);

TR=polyval(tr,x);

RR=polyval(rr,x);

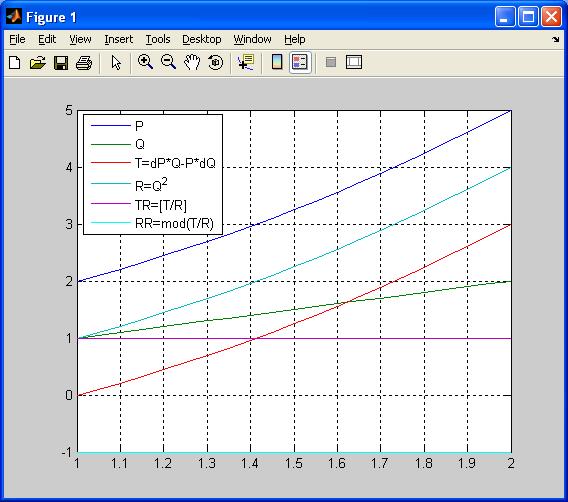
plot(x,P,x,Q,x,T,x,R,x,TR,x,RR),grid on

legend('P','Q','T=dP*Q-P*dQ','R=Q^2','TR=[T/R]','RR=mod(T/R)',0)

 

Результаты счета

ввести коэффициенты полинома P : [a(n),a(n-1),...,a(1),a(0)]=[1 0 1]

ввести коэффициенты полинома Q: [a(n),a(n-1),...,a(1),a(0)]=[1 0]

t =

1 0 -1

r =

1 0 0

tr =

1

rr =

0 0 -1

ввести начальное значение xn=1

ввести конечное значение xk=2

ввести значение n=20

>>