Определение параметров эмпирической зависимости

Лекция 4. Аппроксимирование экспериментальных данных.

При интерполировании функций мы использовали условие равенства значений интерполяционного многочлена и данной функции в известных точках – узлах интерполяции. Это предъявляет высокие требования к точности данных значений функции. В случае обработки опытных данных, полученных в результате наблюдений или измерений, нужно иметь в виду ошибки этих данных. Они могут быть вызваны несовершенством измерительного прибора, субъективными причинами, различными случайными факторами и т. д. Ошибки экспериментальных данных можно условно разбить на три категории по их происхождению и величине: систематические, случайные и грубые.

Систематические ошибки обычно дают отклонение в одну сторону от истинного значения измеряемой величины. Они могут быть постоянными или закономерно изменяться при повторении опыта, и их причина и характер известны. Систематические ошибки могут быть вызваны условиями эксперимента (влажностью, температурой среды и др.), дефектом измерительного прибора, его плохой регулировкой (например, смещением указательной стрелки от нулевого положения) и т. д. Эти ошибки можно устранить наладкой аппаратуры или введением соответствующих поправок.

Случайные ошибки определяются большим числом факторов, которые не могут быть устранены либо достаточно точно учтены при измерениях или обработке результатов. Они имеют случайный (несистематический) характер, дают отклонения от средней величины в ту или другую стороны при повторении измерений и не могут быть устранены в эксперименте, как бы тщательно он ни проводился. С вероятностной точки зрения математическое ожидание случайной ошибки равно нулю. Статистическая обработка экспериментальных данных позволяет определить величину случайной ошибки и довести ее до некоторого приемлемого значения повторением измерений достаточное число раз.

Грубые ошибки явно искажают результат измерения; они чрезмерно большие и обычно пропадают при повторении опыта. Грубые ошибки существенно выходят за пределы случайной ошибки, полученной при статистической обработке. Измерения с такими ошибками отбрасываются и в расчет при окончательной обработке результатов измерений не принимаются.

Таким образом, в экспериментальных данных всегда имеются случайный ошибки. Они, вообще говоря, могут быть уменьшены до сколь угодно малой величины путем многократного повторения опыта. Однако это не всегда целесообразно, поскольку могут потребоваться большие материальные или временные ресурсы. Значительно дешевле и быстрее можно в ряде случаев получить уточненные данные хорошей математической обработкой имеющихся результатов измерений.

В частности, с помощью статистической обработки результатов измерений можно найти закон распределения ошибок измерений, наиболее вероятный диапазон изменения искомой величины (доверительный интервал) и другие параметры.

Эмпирические формулы

Пусть, изучая неизвестную функциональную зависимость между y и x, мы в результате серии экспериментов произвели ряд измерений этих величин и получили таблицу значений

Задача состоит в том, чтобы найти приближенную зависимость

,                                                  (4.1)

значения которой при  мало отличаются от опытных данных y_i. Приближенная функциональная зависимость (4.1), полученная на основании экспериментальных данных, называется эмпирической формулой.

Задача построения эмпирической формулы отличается от задачи интерполирования. График эмпирической зависимости, вообще говоря, не проходит через заданные точки (x_i, y_i), как в случае интерполяции. Это приводит к тому, что экспериментальные данные в некоторой степени сглаживаются, а интерполяционная формула повторила бы все ошибки, имеющиеся в экспериментальных данных.

Построение эмпирической формулы состоит из двух этапов: подбора общего вида этой формулы и определения наилучших значений содержащихся в ней параметров. Общий вид формулы иногда известен из физических соображений. Например, для резистора связь между напряжением u и током i определяется законом Ома: u = R∙ i , где R – активное сопротивление. Задача в данном случае сводится к определению одного неизвестного параметра R.

Если характер зависимости неизвестен, то вид эмпирической формулы может быть произвольным. Предпочтение обычно отдается наиболее простым формулам, обладающим достаточной точностью. Они первоначально выбираются из геометрических соображений: экспериментальные точки наносятся на график и примерно угадывается общий вид зависимости путем сравнения полученной кривой с графиками известных функций (многочлена, показательной или логарифмической функций и т. п.). Успех здесь в значительной мере определяется опытом и интуицией исследователя.

Простейшей эмпирической формулой является линейная зависимость

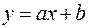.                                          (4.2)

Близость экспериментального распределения точек к линейной зависимости легко просматривается после построения графика данной экспериментальной зависимости. Кроме того, эту зависимость можно проверить путем вычисления значений k_i:

Если при этом k ≈ const, то точки (x_i, y_i) расположены приблизительно на одной прямой, и может быть поставлен вопрос о применимости эмпирической формулы (4.2). Точность такой аппроксимации определяется отклонением величин k_i от постоянного значения. В частном случае равноотстоящих точек x_i (т. е. Δx_i = const) достаточно проверить постоянство разностей Δy_i.

В ряде случаев к линейной зависимости могут быть сведены и другие экспериментальные данные, когда их график в декартовой системе координат не является прямой линией. Это может быть достигнуто путем введения новых переменных ξ , η вместо x, y:

,                             (4.3)

Функции φ(x,y) и ψ(x,y) выбираются такими, чтобы точки (ξ_i, η_i) лежали на некоторой прямой линии в плоскости (ξ, η ). Такое преобразование называется выравниванием данных.

Для получения линейной зависимости

с помощью преобразования (4.3) исходная формула должна быть записана в виде

.

К такому виду легко сводится, например, степенная зависимость 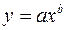(x>0, y>0). Логарифмируя эту формулу, получаем . Полагая , , находим линейную связь: , .

Другой простейшей эмпирической формулой является квадратный трехчлен

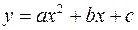.                                            (4.4)

Возможность использования этой формулы для случая равноотстоящих точек x_i можно проверить путем вычисления вторых разностей . При Δ²y_i ≈ const в качестве эмпирической формулы может быть выбрана (4.4).

Определение параметров эмпирической зависимости

Будем считать, что тип эмпирической формулы выбран, и ее можно представить в виде:

                               (4.5)

где φ – известная функция, a_i – неизвестные постоянные параметры. Задача состоит в том, чтобы определить такие значения этих параметров, при которых эмпирическая формула дает хорошее приближение данной функции, значения которой в точках x_i равны y_i (i = 0,1,…, n).

Здесь не ставится условие (как в случае интерполяции) совпадения опытных данных y_i со значениями эмпирической функции (4.5) в точках x_i. Разность между этими значениями (отклонения) обозначим через ε_i. Тогда

.        (4.6)

Задача нахождения наилучших значений параметров a₀, a₁,…, a_m сводится к некоторой минимизации отклонений ε_i. Существует несколько способов решения этой задачи.

Простейшим из них является метод выбранных точек. Он состоит в следующем. По заданным экспериментальным значениям на координатной плоскости X0Y наносится система точек. Затем проводится простейшая плавная линия (например, прямая), которая наиболее близко примыкает к данным точкам. На этой линии выбираются точки, которые, вообще говоря, не принадлежат исходной системе точек. Число выбранных точек должно быть равным количеству искомых параметров эмпирической зависимости. Координаты этих точек тщательно измеряются и используются для записи условия прохождения графика эмпирической функции (4.5) через выбранные точки:

.             (4.7)

Из этой системы уравнений находим значения параметров a₀, a₁,…, a_m.

В частности, если в качестве эмпирической формулы принята линейная зависимость 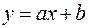, то на этой прямой выбираются точки и , и уравнения (4.7) примут вид

                                    (4.8)

Можно также записать уравнение прямой, проходящей через эти выбранные точки. В этом случае не нужно решать систему (4.8).

Рассмотрим еще один способ определения параметров эмпирической формулы – метод средних. Он состоит в том, что параметры a₀, a₁,…, a_m зависимости (4.5) определяются с использованием условия равенства нулю суммы отклонений (4.6) во всех точках x_i:

         (4.9)

Полученное уравнение служит для определения параметров a₀, a₁,…, a_m. Ясно, что из одного уравнения нельзя однозначно определить все m+1 параметров. Однако, поскольку других условий нет, равенство (4.9) путем группировки отклонений ε_i разбивается на систему, состоящую из m+1 уравнений. Например,

                                    (4.10)

Решая эту систему уравнений, можно найти неизвестные параметры.

Рассмотренные методы определения параметров эмпирической формулы являются сравнительно простыми, однако в ряде случаев получаемые с их помощью аппроксимации не обладают достаточной точностью. В настоящее время одним из наиболее распространенных методов для аппроксимации экспериментальных данных является метод наименьших квадратов.