Создать и изобразить сигналы f(t), представленные прямоугольными импульсами длительностью 1, 5, 20 периодов сигнала s(t).

Для начала рассмотрим пример анализа прямоугольного импульса, приведенный в курсе лекций (пункт 3.1.1).

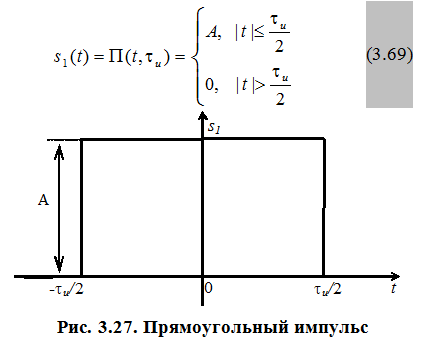
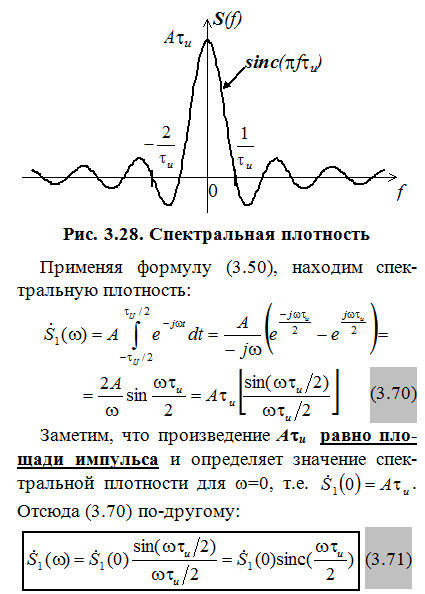
Внимательно посмотрите, как параметры прямоугольного импульса (его амплитуда А и длительность 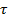 влияют на соответствующие параметры спектральной плотности (ее максимальное значение, места пересечения с осью абсцисс).

Теперь в среде MathCad сгенерируем три прямоугольных импульса единичной амплитуды и длительностью 1, 5, 20 секунд соответственно.

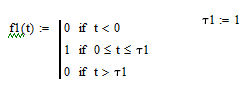
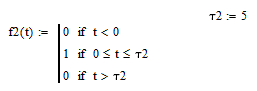
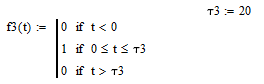
Спектральную плотность для каждого из импульсов рассчитываем по формуле (3.50).

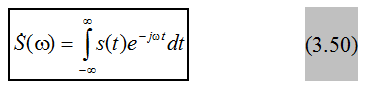
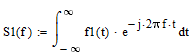
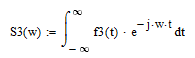
       На рисунках 8 – 10 представлены для каждого импульса его временное отображение, спектральная плотность и модель спектральной плотности.

Рисунок 8а – прямоугольный импульс f1(t)

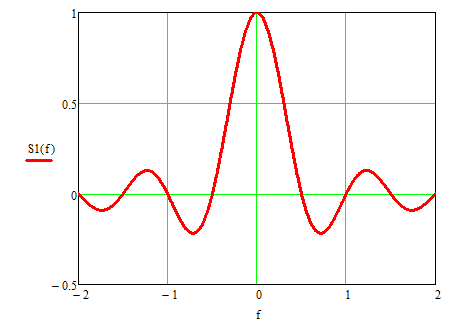
Рисунок 8б – спектральная плотность импульса f1(t)

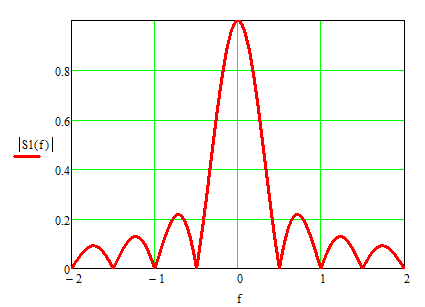
Рисунок 8в – модуль спектральной плотности импульса f1(t) (АЧХ)

Обратите внимание на точки, в которых функция sinc(f) пересекает ось абсцисс, а также на амплитуду этой функции.

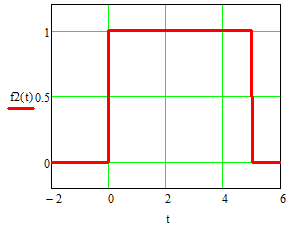
Рисунок 9а – прямоугольный импульс f2(t)

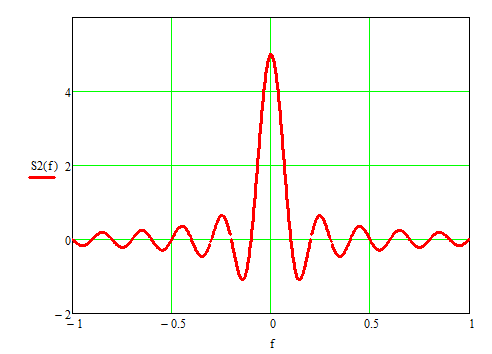
Рисунок 9б – спектральная плотность импульса f2(t)

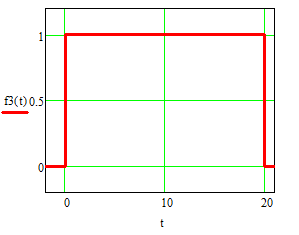
Рисунок 10а – прямоугольный импульс f3(t)

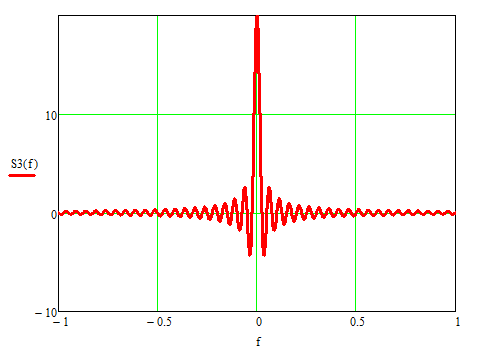
Рисунок 10б - спектральная плотность импульса f3(t)

Как видно из рисунков 8-10, чем продолжительнее во времени прямоугольный импульс, тем «плотнее» функция sinc(f) – его спектральная плотность.

Вопросы к пункту 2:

1. Какой функцией представлена спектральная плотность прямоугольного импульса? Как взаимосвязаны характеристики этой функции и прямоугольного импульса?

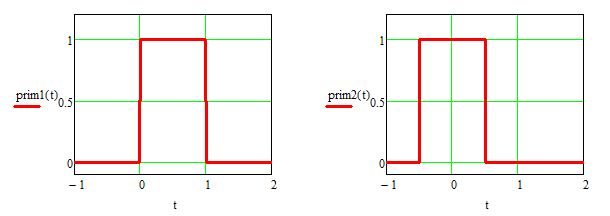
2. Чем будет отличаться спектральная плотность для двух следующих импульсов?

Объясните теорему запаздывания.

3. В чем различие между спектром и спектральной плотностью? Приведите примеры и напишите формулы.

4. Теоремы о спектрах. Объясните теорему «Изменение масштаба времени».

4. Построить сигнал g(t) = s(t)*f(t), а также его спектральную плотность, используя свойства спектров.

Исходный сигнал s(t) периодический и бесконечный. Умножая его на прямоугольный импульс определенной длительности получается выделить несколько необходимых периодов сигнала. Таким образом, получается группа одинаковых, равноотстоящих  импульсов.

Основная теория, необходимая для выполнения задания:

А) Теоремы о спектрах. Произведение двух сигналов (3.3.7 в лекциях).

Б) Пример определения спектра для группы одинаковых равноотстоящих импульсов (3.1.5 в лекциях).

4.1. Выполнить задание для сигнала g1(t) = s(t)*f1(t) – один период.

Перемножим сигналы. Затем воспользуемся формулой (3.50) для расчета спектральной плотности. На рисунке 11а показан сигнал g1(t). На рисунке 11б – модуль его спектральной плотности.

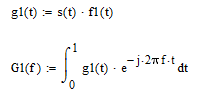
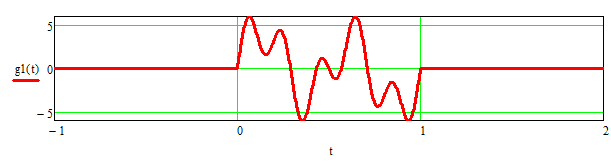
Рисунок 11а – сигнал g1(t), отображающий один период сигнала s(t)

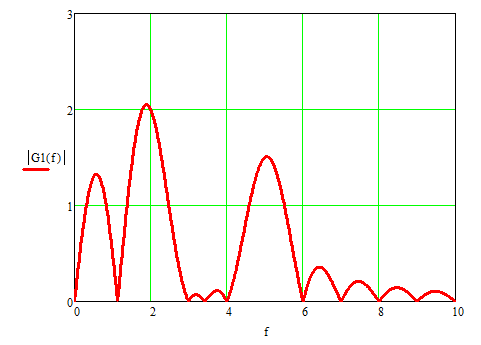
Рисунок 11б – модуль спектральной плотности g1(t)

Теперь немного окунемся в лекции. Документ «03-1Продолжение Главы 3 Примеры определения спектров», пункт 3.1.5 – группа одинаковых и равноотстоящих импульсов.

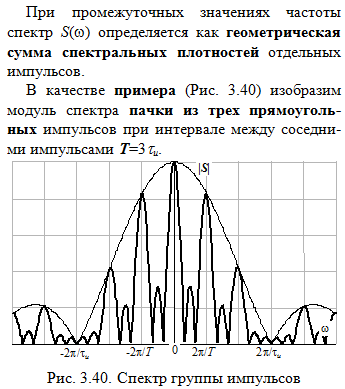
       По сути, сейчас мы будем выполнять ту же самую операцию над сигналом g1(t). В первом случае число N повторений равно 5, во втором – 20.