Алгоритм Флойда-Уоршелла

Рассмотрим структуру кратчайшего пути. В основе алгоритма Флойда-Уоршелла лежат два её свойства.

Во-первых, пусть имеется кратчайший путь

от вершины v₁ до вершины v_k, а также его подпуть

                                     

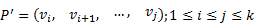
Если P — кратчайший путь от v₁ до v_k, то P’ также является кратчайшим путем от вершины v_i до v_j

Это легко доказать, так как стоимость пути P складывается из стоимости пути P’ и стоимости остальных его частей. Если существует более короткий путь, чем P’, следовательно, заменив P’в Pна него, мы получим путь, более короткий, чем P. Это противоречит утверждению, что для Pсумма пути минимальна.

 

Второе свойство является основой алгоритма. Мы рассматриваем граф G с пронумерованными от 1 до n вершинами {v₁,v₂,… ,v_n} и путь p_ij от v_i до v_j, проходящий через определенное множество разрешенных вершин, ограниченное индексом k.

То есть если k=0, то мы рассматриваем прямые соединения вершин друг с другом, так как множество разрешенных промежуточных вершин рано нулю. Если k=1 — мы рассматриваем пути, проходящие через вершину v₁, при k=2 — через вершины {v₁, v₂}, при k=3 — {v₁, v₃, v₃} и так далее.

Например, у нас есть такой граф (слева) и k=1, то есть в качестве промежуточных узлов разрешен только узел «1». В этом графе при k=1 нет пути p₄₃, но есть при k=2, тогда можно добраться из «4» в «3» через «2» или через «1» и «2».

Рассмотрим кратчайший путь p_ij с разрешенными промежуточными вершинами {1..k-1} стоимостью d_ij. Теперь расширим множество на k- тый элемент, так что множество разрешенных вершин станет {1..k}. При таком расширении возможно 2 исхода:

Случай 1. Элемент k не входит в кратчайший путь p_ij, то есть от добавления дополнительной вершины мы ничего не выиграли и ничего не изменили, а значит, стоимость кратчайшего пути d^k_ij не изменилась, соответственно

d^k_ij = d^k-1_ij — просто перенимаем значение до увеличения k.

Случай 2. Элемент k входит в кратчайший путь p_ij, то есть после добавления новой вершины в можество разрешенных, кратчайший путь изменился и проходит теперь через вершину v_k. Какую стоимость получит новый путь?

Новый кратчайший путь разбит вершиной v_k на p_ik и p_kj, используем первое свойство, согласно ему, p_ik и p_kj также кратчайшие пути от v_i до v_k и от v_k до v_j соответственно. Значит

d^k_ij = d^k_ik + d^k_kj

А так как в этих путях k либо конечный, либо начальный узел, то он не входит в множество промежуточных, соответственно его из него можно удалить:

d^k_ij = d^k-1_ik + d^k-1_kj

Алгоритм

Посмотрим на значение d^k_ij в обоих случаях — верно! оно в обоих случаях складывается из значений d для k-1, а значит, имея начальные (k=0) значения для d, мы сможем рассчитать d для всех последующих значений k. А значения d для k=0 мы знаем, это вес/стоимость рёбер графа, то есть соединений без промежуточных узлов.

При k=n (n — количество вершин) мы получим оптимальные значения d для всех пар вершин.

При увеличении с k-1 до k, какое значение мы сохраним для d^k_ik? Минимумом значений случая 1 и 2, то есть смотрим дешевле ли старый путь или путь с добавлением дополнительной вершины.

Сначала происходит инициализация матрицы кратчайших расстояний D⁰, изначально она совпадает с матрицей смежности, в цикле увеличиваем значение k и пересчитываем матрицу расстояний, из D⁰ получаем D¹, из D¹ — D² и так далее до k=n.

 

Если между двумя какими-то вершинами нет ребра, то в матрице смежности было записано какое-то большое число (достаточно большое, чтобы оно было больше длины любого пути в этом графе); тогда это ребро всегда будет невыгодно брать, и алгоритм сработает правильно.

Задача №257.  Алгоритм Флойда (acmp.ru)

(Время: 1 сек. Память: 16 Мб)

Полный ориентированный взвешенный граф задан матрицей смежности. Постройте матрицу кратчайших путей между его вершинами. Гарантируется, что в графе нет циклов отрицательного веса.

Входные данные

В первой строке записано единственное число N (1 <= N <= 100) - количество вершин графа. В следующих N строках по N чисел - матрица смежности графа (j-ое число в i-ой строке соответствует весу ребра из вершины i в вершину j). Все числа по модулю не превышают 100. На главной диагонали матрицы - всегда нули.

Выходные данные

Выведите N строк по N чисел - матрицу кратчайших расстояний между парами вершин. j-ое число в i-ой строке должно быть равно весу кратчайшего пути из вершины i в вершину j.

Пример

Ввод	Вывод
4 0 5 9 100 100 0 2 8 100 100 0 7 4 100 100 0	0 5 7 13 12 0 2 8 11 16 0 7 4 9 11 0

Решение

Для создания матрицы минимальных путей заменяем каждый элемент матрицы минимумом из непосредственного расстояния между вершинами (в матрице смежности) и суммой длин пути между ними, проходящим через одну из их общих вершин.

#include <iostream>

#define ALL(p) for(p=0; p<n; p++)

using namespace std;

int main() {

int n, d[100][100], i, j, k;

cin >> n;

ALL(i)

     ALL(j)

           cin >> d[i][j];

 

ALL(k)

     ALL(i)

           ALL(j)

                d[i][j] = min (d[i][j], d[i][k] + d[k][j]);

 

ALL(i){

     ALL(j)

           cout << d[i][j] << ' ';

           cout << endl;

     }

}

Задача №258.  Флойд (e-olymp)

Дан ориентированный взвешенный граф. Найти пару вершин, кратчайшее расстояние от одной из которых до другой максимально среди всех пар вершин.

Входные данные

В первой строке записано количество вершин графа n (1 ≤ n ≤ 100). В ней -1 означает отсутствие ребра между вершинами, а любое неотрицательное число - присутствие ребра данного веса.В следующих n строках записано по n чисел - матрица смежности графа (j-ое число в i-ой строке соответствует весу ребра из вершины i в вершину j). На главной диагонали матрицы - всегда нули.

Гарантируется, что в графе есть хотя бы одно ребро.

Выходные данные

Выведите одно число - искомое максимальное кратчайшее расстояние.

Пример

Ввод	Вывод
4 0 5 9 -1 -1 0 2 8 -1-1 0 7 4-1-1 0	16

Решение

#include <iostream>

#define ALL(p) for(p=0; p<n; p++)

using namespace std;

int main() {

int n, d[100][100], i, j, k, maxd = 0;

cin >> n;

ALL(i)

   ALL(j)

       cin >> d[i][j];

ALL(k)

   ALL(i)

     ALL(j)

           if(i != j && d[i][k] != -1 && d[k][j] != -1){

                if(d[i][j] == -1) d[i][j] = d[i][k] + d[k][j];

                else d[i][j] = min(d[i][j], d[i][k] + d[k][j]);

           }

ALL(i)

ALL(j)

     maxd = max(maxd, d[i][j]);

cout << maxd << endl;

}