Динамическое программирование

В теории нет разницы между теорией и практикой. Но на практике она есть

Ян ван де Снепшойт

Решение некоторых задач сводится к нахождению решений подзадач меньшей размерности, которые запоминаются в таблице и никогда более не пересчитываются, а подзадачи большей размерности используют эти уже найденные решения. Такой метод называется динамическим программированием, еще его называют табличным методом. В общей же форме под динамическим программированием понимают процесс пошагового решения задачи оптимизации, при котором на каждом шаге из множества допустимых решений выбирается одно, которое оптимизирует заданную целевую или критериальную функцию.

Задача №259.  Разностные уравнения

Разностное уравнение — уравнение, связывающее значение некоторой неизвестной функции в любой точке с ее значением в одной или нескольких точках, отстоящих от данной на определенный интервал.

Для функции A(n), определённой на множестве натуральных чисел, не превышающих 10000, известно, что

       A(0)= 1

       A(1)= 4

       A(2)= 5

       A(n) = A(n div 2) + A (n div 3) +A(n div 4), для 3 ≤ n ≤ 10000

Операция div в данном случае означает деление нацело. Для заданного значения n найдите A(n).

Решение

Несмотря на то, что, казалось бы, сама постановка задачи подводит нас к рекурсивному решению:

#include <iostream>

int A(int n){

if(n==0) return 1;

if(n==1) return 4;

if(n==2) return 5;

return A(n/2) + A(n/3) + A(n/4);

}

int main(){

int k;

std::cin>>k;

std::cout<<A(k)<<"\n";

}

Такое решение является крайне неэффективным как по времени, так и по использованию памяти. В самом деле, даже для относительно небольшого n = 19 задача решается с помощью тернарного дерева вызовов функции A:

A(19) a

A(9) a

A(6) a

A(4) a

A(2) a

A(1) a

A(1) a

A(3) a

A(2) a

A(1) a

A(1) a

A(1) a

A(0) a

A(4) a

A(3) a

A(2) a

A(1) a

A(1) a

A(0) a

A(2) a

A(1) a

A(1) a

Как можно заметить на схеме, для A(19) произошло 22 вызова функции. Для некоторых значений n (3,4) величина A(n) вычислялась по несколько раз. Более разумным способом решения задачи было бы запоминать найденные значения в массив.

#include <iostream>

int A[10000]={1,4,5};

int main(){

int k;

std::cin >> k;

for(int i = 3; i <= k; i++)

   A[i] = A[i/2] + A[i/3] + A[i/4];

std::cout<< A[k] << "\n";

}

Задача №260.  Гвоздики

(Время: 1 сек. Память: 16 Мб)

На прямой дощечке вбиты гвоздики. Любые два гвоздика можно соединить ниточкой. Требуется соединить некоторые пары гвоздиков ниточками так, чтобы к каждому гвоздику была привязана хотя бы одна ниточка, а суммарная длина всех ниточек была минимальна.

Входные данные

В первой строке записано число N - количество гвоздиков (2 ≤ N ≤ 100). В следующей строке записано N чисел - координаты всех гвоздиков (неотрицательные целые числа, не превосходящие 10000).

Выходные данные

В выходной файл OUTPUT.TXT нужно вывести единственное число - минимальную суммарную длину всех ниточек.

Пример

Ввод	Вывод
6 3  4  12  6  14  13	5

Решение

Вначале упорядочим координаты всех гвоздиков по возрастанию. Если известна оптимальная суммарная длина ниточек для каждого из i-1 гвоздей, то легко определить, что для i-го гвоздя эта величина будет:

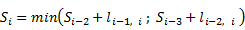
где l_{k, p} – длина ниточки, протянутой от гвоздя k до гвоздя p

#include <iostream>

#include <algorithm>

using namespace std;

int main(){

int n, a[101], s[101];

cin >> n;

for (int i=0; i < n; i++)

cin >> a[i];

sort(a, a + n);

s[0] = 1e9;

s[1] = a[1] - a[0];

s[2] = a[2] - a[0];

for (int i = 3; i < n; i++)

s[i] = min(s[i-2] + a[i] - a[i-1], s[i-3] + a[i] - a[i-2]);

cout << s[n-1];

}

Задача №261.  Уменьшающееся число (e-olimp)

(Лимит времени 1 секунда. Лимит использования памяти 64 Мб)

Над целым числом можно производить следующие операции:

1. Если число делится на 3, то делить его на 3;

2. Если число делится на 2, то делить его на 2;

3. Вычитать 1.

По заданному натуральному числу n найти наименьшее количество операций, после выполнения которых получится 1.

Входные данные

Каждая строка содержит одно натуральное число n (1 ≤ n ≤ 10⁶).

Выходные данные

Для каждого значения n в отдельной строке вывести наименьшее количество операций, после выполнения которых получится 1.

Пример

Ввод	Вывод
1 5 10	0 3 3

Решение

Обозначим за m максимальное число, для которого ответ уже посчитан. Для того чтобы ускорить процесс вычислений, для первых 1000 значений ответ найдём сразу. Далее величину m будем увеличивать при необходимости, заполняя недостающие значения от последнего значения m до n.

#include <iostream>

int n, m, a[1000001] = {0, 0, 1, 1,};

 

void calc(int l, int r){        // подсчет ответов от l до r

for(int i = l, minx; i <= r; i++){

   minx = a[i-1];

   if (i%2==0 && a[i/2]<minx) minx = a[i/2];

   if (i%3==0 && a[i/3]<minx) minx = a[i/3];

   a[i] = minx + 1;

}

m = r;

}

 

int main(){

calc(3, 1000);              // предварительные вычисления

 

while(std::cin >> n){

   if(n > m) calc(m, n);

   std::cout << a[n] << '\n';

}

}

Задача №262.  Максимальная подпоследовательность (acmp.ru)

(Время: 1 сек. Память: 32 Мб)

Дана числовая последовательность, требуется найти длину наибольшей возрастающей подпоследовательности.

Подпоследовательностью назовём произвольную группу элементов исходной последовательности с сохранением порядка их следования (элементы могут идти не подряд)

Входные данные

В первой строке записано число N - длина последовательности (1 <= N <= 1000). Во второй строке записана сама последовательность (через пробел). Числа последовательности - целые числа, не превосходящие 10000 по модулю.

Выходные данные

Требуется вывести наибольшую длину возрастающей подпоследовательности.

Пример

Ввод	Вывод
6 3  29  5  5  28  6	3

Решение

Заведём вспомогательный массив d_i, для хранения длины самой большой возрастающей подпоследовательности до элемента с индексом i включительно.

Для текущего индекса i, элементы d_i принимают значение 1, если до индекса i в массиве a не было элементов меньших a_i. Если же таковые элементы a_jнашлись, то d_i = d_j + 1

Ответом задачу будет наибольший элемент массива d_i.

#include <iostream>

int n, a[1000], d[1000], x, i, j;

int main(){

std::cin >> n;

for (i = 0; i < n; i++) {

   std::cin >> a[i];

    d[i] = 1;

    for (j = 0; j < i; j++)

       if (a[j] < a[i] && d[i] <= d[j])

           d[i] = 1 + d[j];

    if(d[i] > x) x = d[i];

}

std::cout << x;

}

Можно получить более быстрое решение для больших значений N (например, 10⁵), поскольку предложенный алгоритм за 1 секунду не справится и даст TLE.

Идея заключается в следующем: заведём вспомогательный массив U_p в котором будем хранить величину максимального элемента возрастающей подпоследовательности длины p. При этом для двух возрастающих подпоследовательностей длины p будем выбирать меньшее из этих двух чисел.

Очевидно, что массив U будет строго возрастающим. Так, например, для массива из 8 целых чисел

70 80 1 2 90 3 5  -1

нахождение элементов массива U будет происходить так

u[0] = 70

u[1] = 80

u[0] = 1

u[1] = 2

u[2] = 90

u[2] = 3

u[3] = 5

u[0] = -1

i	0	1	2	3	…
Ui	-1	2	3	5	…

Каждый следующий элемент исходного массива A легко находить в упорядоченном массиве U методом бинарного поиска (рассматривался в главе «Массивы»). Очевидно, индекс последнего найденного элемента, увеличенный на 1, будет ответом к задаче. Для более быстрого ввода и вывода такого большого набора чисел воспользуемся библиотекой stdio.

Автор решения: Козлов А. И.

#include <stdio.h>

 

int n, a[100000], u[100000], ans = 1, t;

 

int bs(int p) {      // бинарный поиск p в массиве u

int l = 0, r = ans, c;

while (l < r) {

   c = (l + r) / 2;

   if (u[c] >= p) r = c; else l = c + 1;

}

return l;

}

 

int main() {

scanf("%d", &n);

for (int i = 0; i < n; i++)

   scanf("%d", &a[i]);

   

u[0] = a[0];

for (int i = 1; i < n; i++) {

   t = bs(a[i]);

   u[t] = a[i];

   if (t == ans) ans++;

}

printf("%d\n", ans);

}

Задача №263.  Голодная черепашка

Черепаха находится в левом верхнем углу таблицы и мечтает попасть в правый нижний. Ползти она может только вправо либо вниз. В клетке (i,j) содержится F_i,j еды. Помогите черепахе достичь цели, собрав как можно больше еды.

Вывести единственное число – максимально возможное количество собранной еды по пути черепахи

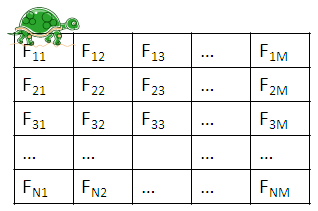
Рис. 48 Иллюстрация к задаче "Голодная черепашка"

Решение

Очевидно, что самым неэффективным алгоритмом решения задачи будет полный перебор всех вариантов пути черепахи как с точки зрения времени выполнения, так и по затратам памяти. Воспользуемся динамическим программированием для решения данной задачи.

Определим, какое максимальное значение по пути черепахи к клетке может быть в ней собрано. Начать следует с верхней горизонтали и левой вертикали. Например, рассмотрим такую матрицу и выделим в ней цветомячейки, в которые можно прийти единственным образом, рассчитав, сколько еды при этом съест черепаха.

2	3	2	4	7		2	5	7	11	18
4	1	1	6	9		6
0	5	3	12	6		6
8	2	2	8	1		14

В каждую из незаполненных ячеек можно прийти с соседней клетки слева и соседней сверху. Например, в ячейку с 3 единицами еды можно прийти из соседних клеток, по дороге к которым черепаха может съесть 17 и 15 единиц еды соответственно.

17

15

3

17

15

20

Очевидно, что черепаха предпочтёт попасть в заданную клетку из соседней слева (17), а не соседней сверху (15). Таким образом, добравшись до этой ячейки, черепаха сможет съесть максимальное количество еды 20.

Завершим заполнение матрицы из предыдущего примера:

2	5	7	11	18
6	7	8	17	27
6	12	15	29	35
14	14	17	37	38

Код, реализующий поставленную задачу, будет выглядеть следующим образом:

#include <iostream>

#define N 4                               // строки

#define M 5                               // столбцы

#define MAX(a, b) ((a) > (b) ? (a) : (b))

int a[N][M]={2, 3, 2, 4, 7,

        4, 1, 1, 6, 9,

        0, 5, 3, 12, 6,

        8, 2, 2, 8, 1};

int main() {

for(int i = 0; i < N; i++)

   for(int j = 0; j < M;j++)

       a[i][j] += MAX((i ? a[i-1][j] : 0),

                      (j ? a[i][j-1] : 0));

std::cout << a[N-1][M-1];

}

У этой задачи существует множество вариаций.

Задача №264.  Минимальный путь в таблице (acmp.ru)

(Время: 1 сек. Память: 16 Мб)

В прямоугольной таблице N×M (в каждой клетке которой записано некоторое число) в начале игрок находится в левой верхней клетке. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). При проходе через клетку с игрока берут столько у.е., какое число записано в этой клетке (деньги берут также за первую и последнюю клетки его пути).

Требуется найти минимальную сумму у.е., заплатив которую игрок может попасть в правый нижний угол.

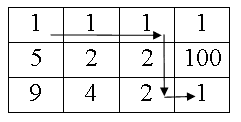
Рис. 49. Минимальный путь в таблице

Входные данные

Во входном файле INPUT.TXT задано два числа N и M - размеры таблицы (1 ≤ N ≤ 20, 1 ≤ M ≤20). Затем идет N строк по M чисел в каждой - размеры штрафов в у.е. за прохождение через соответствующие клетки (числа от 0 до 100).

Выходные данные

В выходной файл OUTPUT.TXT выведите минимальную сумму, потратив которую можно попасть в правый нижний угол.

Пример

№	INPUT.TXT	OUTPUT.TXT
1	3 4 1  1  1  1 5  2  2 100 9  4  2  1	8
2	5 5 1  1  1  1  1 3  100 100 100 100 1  1  1  1  1 2  2  2  2  1 1  1  1  1  1	11

Решение

#include <fstream>

using namespace std;

int n, m, a[20][20], x, y;

int main() {

ifstream cin("input.txt");

ofstream cout("output.txt");

cin >> n >> m;

for(int i = 0; i < n; i++)

     for(int j = 0; j < m; j++){

           cin >> a[i][j];

           if(!i && !j) x = y = 0;

           else{

                y = i ? a[i-1][j] : 1e9;

                x = j ? a[i][j-1] : 1e9;

           }

           a[i][j] += min(x, y);

     }

cout << a[--n][--m];

}

Как можно найти не только сумму оптимального пути (максимум или минимум), но и восстановить сам путь? Рассмотрим следующую задачу.

Задача №265.  Маршрут

(Лимит времени 1 с, лимит памяти 64 MB)

В таблице из N строк и N столбцов клетки заполнены цифрами от 0 до 9. Требуется найти такой путь из клетки (1, 1) в клетку (N, N), чтобы сумма цифр в клетках, через которые он пролегает, была минимальной; из любой клетки ходить можно только вниз или вправо.

Входные данные

В первой строке находится число N (2 ≤ N ≤ 250). В следующих N строках содержатся по N цифр без пробелов.

Выходные данные

Выводятся N строк по N символов. Символ решётка показывает, что маршрут проходит через эту клетку, а точка - что не проходит. Если путей с минимальной суммой цифр несколько, вывести любой.

Входные данные	Выходные данные
3 943 216 091	#.. ### ..#

Решение

Как и в предыдущей задаче, вначале потребуется определить сумму на оптимальном пути. Она будет записана в последнюю ячейку таблицы. Затем определим, из какой именно клетки мы туда попали – т.е. из соседней сверху и соседней слева выберем ту, где наименьшее значение и т.д.

#include <iostream>

#define SIZE 251

using namespace std;

 

int a[SIZE][SIZE], n, i, j;

char road[SIZE][SIZE];

 

bool bestleft(){                // предпочтительнее идти влево

if (!i) return false;

if (!j) return true;

return a[i-1][j] < a[i][j-1];

}

 

int main() {

cin >> n;

for (i = 0; i < n; i++) // чтение данных

   for (j = 0; j < n; j++) {

       cin >> road[i][j];

       a[i][j] = road[i][j] - '0';

}

for(i = 0; i < n; i++) // определяем наилучшую сумму

   for(j = 0; j < n; j++){

       if (!i && j) a[i][j] += a[i][j-1];          

       if (i && !j) a[i][j] += a[i-1][j];

       if (i && j) a[i][j] += min(a[i-1][j] , a[i][j-1]);

   }

for (i = 0; i < n; i++)

   for (j = 0; j < n; j++)

       road[i][j] = '.';

i = j = n - 1;

while(i || j){        // восстанавливаем путь

   road[i][j] = '#';

   if(bestleft()) i--;

   else j--;

};

road[0][0] = '#';

for (i = 0; i < n; i++) // вывод результата

   for (j = 0; j < n; j++)

       cout << road[i][j] << (j==n-1 ? "\n" : "");

}

Задача №266.  Только вправо или вниз (acmp.ru)

(Время: 1 сек. Память: 16 Мб)

Игровое поле N × M заполняется целыми числами, одно неотрицательное целое число в каждой клетке. Цель игры состоит в том, чтобы пройти по любому разрешенному пути от верхнего левого угла до правого нижнего. Целое число в каждой клетке указывает, какой длины шаг должен быть из текущей клетки. Все шаги могут быть или направо или вниз. Если в результате какого-либо шага игрок покидает пределы поля, такой шаг запрещается.

На рисунке приведен пример игрового поля 3×4, где левая верхняя и правая нижняя клетка таблицы – начало и конец пути соответственно. На следующих трёх таблицах показаны три возможных пути от начала до цели.

2 1 1 2   2         2   1     2   1 2 3 2 1 44                 1             3 1 1 0   3     0       1 0         0

 Требуется написать программу, которая определит число различных вариантов путей от верхнего левого угла до правого нижнего.

Входные данные

В первой строке размеры поля N (1 ≤ N ≤ 70) и M (1 ≤ M ≤ 70). В последующих N строках входного файла, каждая из которых описывает отдельную строку игрового поля, записаны через пробел по M целых чисел – длины шагов из клеток данной строки.

Выходные данные

Одно число - число различных вариантов путей от верхнего левого угла до правого нижнего. Для каждого поля будет менее чем 231 различных путей.

Пример

Ввод	Вывод
3  4 2  1  1  2 3  2  1  44 3  1  1  0	3

Решение

Будем считать, что в начальную клетку существует ровно один способ попасть. Если в клетку с координатами (i, j) можно попасть из клетки (x, y), то будем добавлять к числу способов попасть туда A_ij величину A_xy. Единственный «подводный камень» задачи заключается в том, чтобы исключить из рассмотрения клетки, в которые записано число 0, поскольку к величине A_ij будет добавляться её значение повторно.

#include <iostream>

int a[70][70] = {1,}, x, n, m, i, j;

int main(){

std::cin >> n >> m;

for(i = 0; i < n; i++)

     for(j = 0; j < m; j++){

           std::cin >> x;

           if(i+x < n  &&  x) a[i+x][j] += a[i][j];

           if(j+x < m  &&  x) a[i][j+x] += a[i][j];

     }

std::cout << a[n-1][m-1];

}

Задача №267.  Ферзя в угол! (acmp.ru)

(Время: 1 сек. Память : 16 Мб)

Рассмотрим бесконечную вправо и вверх шахматную доску, на которой стоит ферзь. Двое по очереди двигают этого ферзя. Разрешается двигать ферзя только вниз, влево или по диагонали вниз влево. Цель игры – задвинуть ферзя в угол, то есть клетку с координатами (1, 1). На рисунке показаны разрешенные движения ферзя.

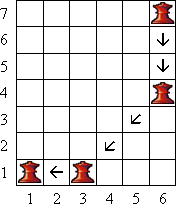
Рис. 50. Иллюстрация к задаче "Ферзя в угол"

Требуется написать программу, которая найдет номер игрока, который выиграет при правильной игре.

Входные данные

Координаты ферзя перед первым ходом - два числа M и N, записанные через пробел (1 ≤ M, N ≤ 250).

Выходные данные

Одно число - найденный номер победителя.

Примеры

№	Ввод	Вывод
1	3  2	2
2	6  7	1

Решение

Заведём двумерный массив, который будем заполнять единицами либо двойками – номерами того игрока, который для данной клетки обладает выигрышной стратегией:

#include <iostream>

int x, y, a[250][250];

void fill(int p, int q){

a[p][q] = 2;

for(int i = 1; i < 249; i++){

   if(p + i < 250) a[p+i][q] = 1;

   if(q + i < 250) a[p][q+i] = 1;

   if(p + i < 250 && q + i < 250) a[p+i][q+i] = 1;

}

}

int main() {

for(int i = 0; i < 250; i++)

   for(int j = 0; j < 250; j++)

       if(!a[i][j]) fill(i, j);

std::cin >> x >> y;

std::cout << a[--y][--x];

}

Задача №268.  Прямоугольник (acmp.ru)

(Время: 1 сек. Память: 16 Мб)

Задан целочисленный прямоугольный массив MxN. Необходимо определить прямоугольную область данного массива, сумма элементов которого максимальна.

Входные данные

В первой строке записаны два натуральных числа N и M (1 ≤ N, M ≤ 100) – количество строк и столбцов прямоугольной матрицы. Далее идут N строк по M чисел, записанных через пробел – элементы массива, целые числа, не превосходящие 100 по абсолютной величине.

Выходные данные

Вывести целое число – сумму элементов найденного прямоугольного подмассива.

Примеры

№	Ввод	Вывод
1	2  3 5  0  9 1  2  7	24
2	4  5 -7  8  -1  0  -2 2  -9  2  4  -6 -7  0  6  8  1 4  -8  -1  0  -6	20

Решение

Очевидно, что самым неэффективным алгоритмом решения данной задачи будет полный перебор всех прямоугольников. Вместо этого применим подход, который называется суммы на префиксах. Будем записывать в двухмерный массив не сами значения, а сумму всех элементов исходной матрицы, которые входят в прямоугольную область от начала матрицы до текущего элемента включительно. Таким образом, матрица из первого примера

5	0	9
1	2	7

будет преобразована к виду:

5	5	14
6	8	24

Теперь мы можем найти сумму прямоугольного набора элементов исходной матрицы от (p, q) до (i, j) за одно арифметическое действие.

A p-1,q-1         A p-1, j           A p, q       A p, j                                                 A i,q-1 A i, q       A i, j

Для того чтобы найти сумму в данном прямоугольнике, надо от суммы A[i][j] отнять две суммы A[i][q-1] и A[p-1][j] и добавить сумму A[p-1][q-1], поскольку эта величина входила в обе вычитаемые суммы и т.о. была посчитана дважды.

Временная сложность представленного алгоритма O(N²×M²)

#include <iostream>

int main() {

long long a[101][101], n, m, i, j, p, q, s, ans = -100;

std::cin >> n >> m;

for(i = 0; i < n; i++)

   for(j = 0; j < m; j++){

       std::cin >> a[i][j];

       a[i][j] += (i ? a[i-1][j] : 0) + (j ? a[i][j-1] : 0)

                   - ( i && j ? a[i-1][j-1] : 0);

   }

for(i = 0; i < n; i++)

   for(j = 0; j < m; j++)

       for(p = 0; p <= i; p++)

           for(q = 0; q <= j; q++){

               s = a[i][j] - (p ? a[p-1][j] : 0)

                       - (q ? a[i][q-1] : 0)

                       + (p && q ? a[p-1][q-1] : 0);

               if (s > ans) ans = s;

           }

std::cout << ans;   

}

Задача №269.  Новый Лабиринт Амбера (e-olymp)

(Лимит времени 0,5 c; память 64 Мб)

Как-то Корвину – принцу Амбера, по каким-то важным делам срочно понадобилось попасть в самую далекую тень, которую он только знал. Как всем известно, самый быстрый способ путешествия для принцев Амбера – это Лабиринт Амбера. Но у Корвина были настолько важные дела, что он не хотел тратить время на спуск в подземелье (именно там находится Амберский Лабиринт). Поэтому он решил воспользоваться Новым Лабиринтом, который нарисовал Дворкин. Но этот Лабиринт не так прост, как кажется…

Новый Лабиринт имеет вид последовательных ячеек, идущих друг за другом, пронумерованных от 1 до N. Из ячейки под номером i можно попасть в ячейки под номерами i+2 (если i+2 ≤ N) и i+3 (если i+3 ≤ N). На каждой ячейке лежит какое-то количество золотых монет k_i. Для того чтобы пройти лабиринт нужно, начиная ходить из-за границ лабиринта (с нулевой ячейки) продвигаться по выше описанным правилам, при этом подбирая все монетки на ячейках, на которых вы делаете промежуточные остановки. Конечная цель путешествия – попасть на ячейку с номером N. Дальнейшее путешествие (в любое место Вселенной) возможно лишь тогда, когда достигнув ячейки с номером N, вы соберете максимально количество монеток. Напишите программу, которая поможет Корвину узнать, какое максимальное количество монеток можно собрать, проходя Новый Лабиринт Амбера.

Входные данные

В первой строке входного файла содержится натуральное число N (2 ≤ N ≤ 100000), а во второй N целых чисел, разделенных одним пробелом, k_i – количество монеток лежащих в ячейке с номером i (0 ≤ k_i ≤ 1000).

Выходные данные

В выходной файл вывести одно целое число – максимальное количество монеток, которое можно собрать, проходя лабиринт.

Примеры

№	Ввод	Вывод
1	5 1000  2  3  1  3	6
2	2 1  2	2
3	4 1  3  100  0	3

Решение

#include <iostream>

using namespace std;

int m[100001];

int main(){

int n;

cin >> n;

for(int i = 1; i <= n; i++)

   cin >> m[i];

 

m[1] = 0;

for(int i = 3; i <= n; i++)

   m[i] += max(m[i-2], m[i-3]);

 

cout << m[n];

}

Задача №270.  Распределение оценок (e-olymp)

Лимит времени 1 секунда. Лимит использования памяти 64 MiB

В экзаменационный период студент сдал n предметов, за которые в сумме получил t баллов. Наименьший балл, при котором ставится зачет по каждому предмету, равен p. Вам следует подсчитать количество способов, которыми студент мог получить баллы на экзаменах. Например, если n = 3, t = 34 и p = 10, то баллы по трем предметам могли распределиться следующими способами:

	Предмет 1	Предмет 2	Предмет 3
1	14	10	10
2	13	11	10
3	13	10	11
4	12	11	11
5	12	10	12
6	11	11	12
7	11	10	13
8	10	11	13
9	10	10	14
10	11	12	11
11	10	12	12
12	12	12	10
13	10	13	11
14	11	13	10
15	10	14	10

Студент может сдать сессию 15 способами.

Входные данные

Первая строка содержит количество тестов. Каждый тест содержит в одной строке три числа n, t и p, значения каждого из которых не больше 70.

Выходные данные

Для каждого теста вывести количество способов, которыми студент мог получить баллы на экзаменах. Ответ всегда является знаковым 32-битовым целым числом.

Ввод	Вывод
2 3 34 10 3 34 11	15 3

Решение

#include <iostream>

#define SIZE 4901

int test, n, t, p, i, j, a[SIZE][SIZE];

int main(){

std::cin >> test;

for(i = 0; i < 70; i++) a[0][i] = 1;

for(; test--;){

   std::cin >> n >> t >> p;

   for(i = 1; i < n*t; i++)

       for(j = 0; j < n*t; j++)

           a[i][j] = 0;

   for(i = 1; i < n; i++)

       for(j = (i+1)*p; j <= t; j++)

          a[i][j] = a[i][j-1] + a[i-1][j-p];     

   std::cout << a[n-1][t] << std::endl;

}

}

Задача №271.  Компьютерная игра – 2 (acmp.ru)

Вы можете вспомнить хоть одного своего знакомого до двадцатилетнего возраста, который в детстве не играл в компьютерные игры? Если да, то может быть вы и сами не знакомы с этим развлечением? Впрочем, трудностей при решении этой задачи это создать не должно.

Во многих старых играх с двумерной графикой можно столкнуться с подобной ситуацией. Какой-нибудь герой прыгает по платформам (или островкам), которые висят в воздухе. Он должен перебраться от одного края экрана до другого. При этом при прыжке с одной платформы на соседнюю, у героя уходит |y2-y1| единиц энергии, где y1 и y2 – высоты, на которых расположены эти платформы. Кроме того, у героя есть суперприем, который позволяет перескочить через платформу, но на это затрачивается 3*|y3-y1| единиц энергии. Конечно же, энергию следует расходовать максимально экономно.

Предположим, что вам известны координаты всех платформ в порядке от левого края до правого. Сможете ли вы найти, какое минимальное количество энергии потребуется герою, чтобы добраться с первой платформы до последней?

Входные данные

В первой строке входного файла INPUT.TXT записано количество платформ n (1 ≤ n ≤ 30000). Вторая строка содержит n натуральных чисел, не превосходящих 30000 – высоты, на которых располагаются платформы.

Выходные данные

В выходной файл OUTPUT.TXT запишите единственное число – минимальное количество энергии, которую должен потратить игрок на преодоление платформ (конечно же в предположении, что cheat-коды использовать нельзя).

Пример

INPUT.TXT	OUTPUT.TXT
3 1  5  10	9
3 1  5  2	3

Решение

Эта задача по способу решения очень похожа на предыдущую:

#include <fstream>

#include <cstdlib>

#define SIZE 30000

using namespace std;

int h[SIZE], e[SIZE] = {0};

int main(){

ifstream cin("input.txt");

ofstream cout("output.txt");

int n;

cin >> n;

for(int i = 0; i < n; i++) cin >> h[i];

e[1] = abs(h[1] - h[0]);

for(int i=2; i<n; i++)

   e[i] = min(e[i-2] + 3*abs(h[i] - h[i-2]),

              e[i-1] + abs(h[i] - h[i-1]));

cout << e[n-1];

}

Задача №272.  Фермер (acmp.ru)

(Время: 1 сек. Память: 16 Мб)

Фермер решил на своем квадратном участке земли вспахать пашню квадратной формы максимальной площади, т.к. он посчитал, что именно квадратная форма пашни наиболее удобна для обработки. Но на его участке присутствуют деревья и хозяйственные постройки, которые он никуда не хочет переносить, а так же иные места, не пригодные для пашни. Для удобства он составил квадратную карту местности NxN в форме матрицы и пометил нулями непригодные для пашни зоны, в остальные зоны он поставил единицу.

Необходимо помочь фермеру определить максимальную площадь пашни.

Входные данные

В первой строке записано единственное натуральное число N (1 ≤ N ≤ 1000) – длина стороны квадратного участка фермы. Далее, следует N строк, в каждой из которых находится последовательность (без пробелов) нулей и единиц, описывающих ферму.

Выходные данные

Необходимо вывести максимально возможную площадь пашни.

Пример

Ввод	Вывод
7 1101101 1111110 1011100 0011100 1000010 1100111 1001110	9

Решение

Идея решения задачи состоит в следующем. Для каждой ячейки матрицы поля рассмотрим три соседние с ней (сверху, слева и слева сверху). Квадрат из них можно построить только если они все ненулевые. Если все соседи равны 1, то в ячейку матрицы поставим 2. Если соседние не меньше 2, то в ячейку поставим 3 и т.д. Таким образом мы вычисляем размер стороны квадратной пашни, которую удастся построить от заданной клетки вверх и влево.

#include <iostream>

#define SIZE 1000

using namespace std;

int n, dp[SIZE][SIZE]={0,}, t1, t2, t3, mx = 0;

int main(){

string s;

cin >> n;

for(int i=0; i<n; i++){

   cin >> s;

   for(int j = 0; j<n; j++){

       dp[i][j] = s[j] - '0';

       if(dp[i][j]){

           t1 = i ? dp[i-1][j] : 0;  //проверка наличия

           t2 = j ? dp[i][j-1] : 0;  //соседних клеток

           t3 = i && j ? dp[i-1][j-1] : 0;

           dp[i][j] += min(t1, min(t2,t3));

       }

       if(dp[i][j] > mx) mx = dp[i][j];

   }

}

cout << mx * mx;

}

 

Задача №273.  Лестница

Предположим, некто, двигаясь по лестнице способен переступать со ступеньки на ступеньку, либо перескакивать через 1 ступеньку. Сколькими способами Q он может добраться с нижнего уровня (высота 0 ступенек) до вершины лестницы из N ступеней.

Пример

При N = 3 таких способов окажется 3. Эти способы с номерами ступенек выглядят так 1-2-3, 2-3, 1-3.

Идея решения

N	Q	Способы
1	1	1
2	2	1-2, 2
3	3	1-2-3, 2-3, 1-3
4	5	1-2-3-4, 2-3-4, 1-3-4, 1-2-4, 2-4
5	8	1-2-3-4-5, 2-3-4-5, 1-3-4-5, 1-2-4-5, 2-4-5, 1-2-3-5, 2-3-5, 1-3-5
6	13	1-2-3-4-5-6, 2-3-4-5-6, 1-3-4-5-6, 1-2-4-5-6, 2-4-5-6, 1-2-3-5-6, 2-3-5-6, 1-3-5-6, 1-2-3-4-6, 2-3-4-6, 1-3-4-6, 1-2-4-6, 2-4-6

и т.д. Как видно, на любую ступеньку K, начиная с номера 3, можно прийти со ступенек K-1 и К-2. Например, все способы оказаться на ступеньке номер 6 получаются «дописыванием» 6 к способам дойти до 5 и к способам дойти до 4. Т.е.

       Q(K) = Q(K-1) + Q(K-2)

а сама последовательность Q(K) соответствует ряду Фибоначчи.

Задача №274.  Сломанная лестница

Усложним предыдущую задачу. Допустим, часть ступенек на лестнице разрушена. Сколько в таком случае имеется способов достигнуть вершины?

Входные данные

В первой строке единственное число N, не превышающее 20. Во второй строке Nчисел

S₁ S₂ S₃ … S_N ,

записанных через пробел, где S_i=0, если i-ая ступенька сломана и 1, если целая.

Выходные данные

Единственное число Q– количество способов достигнуть вершины.

Задача №275.  Заяц на лестнице

В нашем зоопарке появился заяц. Его поместили в клетку, и чтобы ему не было скучно, директор зоопарка распорядился поставить в его клетке лесенку. Теперь наш зайчик может прыгать по лесенке вверх, перепрыгивая через ступеньки. Лестница имеет определенное количество ступенек N. Заяц может одним прыжком преодолеть не более К ступенек. Для разнообразия зайчик пытается каждый раз найти новый путь к вершине лестницы. Директору любопытно, сколько различных способов есть у зайца добраться до вершины лестницы при заданных значениях K и N. Помогите директору написать программу, которая поможет вычислить это количество. Например, если K=3 и N=4, то существуют следующие маршруты: 1+1+1+1, 1+1+2, 1+2+1, 2+1+1, 2+2, 1+3, 3+1. Т.е. при данных значениях у зайца всего 7 различных маршрутов добраться до вершины лестницы