Основные формулы комбинаторики

Правило умножения: Если объект A₁можно выбрать k₁способами, A₂–k₂способами, …, A_n–k_nспособами, то их комбинацию A₁A₂…A_n можно выбрать k₁×k₁×…×k_nспособами.

Например, для участия в школьном утреннике из класса требуется в качестве ведущих отобрать одного темноволосого учащегося, одного рыжего и одного блондина. В классе 12 темноволосых учеников, 7 светловолосых и 3 рыжих. Всего имеется 12×7×3=252 способа выбрать ведущих.

Правило сложения: Если объект A₁можно выбрать k₁способами, A₂–k₂способами, …, A_n–k_nспособами, а их выборы несовместимы, то выбрать объект A₁ или A₂или … A_nможно k₁+k₁+…+k_nспособами.

Например, для участия в забеге спортсмен имеет 3 пары кроссовок и две пары кед. Сколько существует способов подобрать обувь? Очевидно, спортсмен не может одеть две пары обуви одновременно, т.е. по правилу сложения имеется 3+2=5 способов.

Перестановки: Пусть имеется n различных объектов.

Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно

Символ n! называется факториалом и обозначает произведение всех целых чисел от 1 до n. По определению, считают, что 0!=1.

Например, расставить 3 горшка с цветами по 3 разным подоконникам существует 3!=6 способов.

Размещения: Пусть имеется n различных объектов.

Будем выбирать из них m объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из n объектов по m, а их число равно

Например, выбрать из 4 кандидатур старосту класса и заместителя старосты существует

способов[40].

Сочетания: Пусть имеется nразличных объектов.

Будем выбирать из них m объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из n объектов по m, а их число равно

Например, если нужно назначить 3 дежурных из 10 человек, то таких способов существует .

Легко заметить, что . В самом деле, возвращаясь к приведенному примеру, способов выбрать 3 дежурных из 10 ровно столько же, сколько способов выбрать 7 учащихся из 10, которые дежурить не будут.

Задача №284.  Садовник-художник

(Время: 1 сек. Память: 16 Мб)

Садовник посадил N деревьев в один ряд. После посадки деревьев садовнику нужно их покрасить. В его распоряжении есть краска трех цветов: белая, синяя и оранжевая. Сколько способов покраски деревьев есть у него, если никакие два соседних дерева нельзя красить в одинаковый цвет?

Входные данные

В единственной строке записано одно натуральное число - количество деревьев N (1 ≤ N ≤ 50).

Выходные данные

В единственную строку нужно вывести одно число - количество способов покраски.

Пример

Ввод	Вывод
3	12

Решение

Первое дерево можно покрасить 3 способами. Каждое следующее – двумя. Т.о. общее число способов покраски по правилу умножения

#include <iostream>

int main(){

int n;

std::cin >> n;

std::cout << 3 * (1LL << --n);

}

Для n»50 результат окажется больше максимально возможного в типе int. Поэтому применим литерал 1 LL– единица в типе longlong. Для возведения двойки в степень проще и удобнее всего использовать операцию побитового сдвига влево.

Задача №285.  Треугольник Паскаля

Для разложения на слагаемые некоторой степени двучлена используется формула бинома Ньютона

где биномиальные коэффициенты

Например,

Выведите все биномиальные коэффициенты для степени n от 0 до 40.

Если продлить такую таблицу, то она называется «треугольником Паскаля».

Решение

Очевидно, самый неудачный способ решения задачи - считать число сочетаний непосредственно по формуле. Считать три факториала, над которыми затем производить операции умножения и деления – плохая идея. Воспользуемся рекуррентным соотношением, как поступают математики, считающие биномиальные коэффициенты вручную.

Определив, что для m = 0 или для m = n , построим рекурсивное решение.

#include <iostream>

#define N 20

using namespace std;

 

int C(int m, int n){

if(m==0 || m==n) return 1;

return C(m, n-1) + C(m-1, n-1);

}

 

int main() {

for(int i = 0; i < N; i++){

   for(int j = 0; j <= i; j++) cout << C(j,i) << " ";

   cout << endl;

}

return 0;

}

При N>30 решение становится очень долгим и затратным по памяти. Воспользуемся методом динамического программирования, чтобы его улучшить.

#include <iostream>

#define N 40

using namespace std;

unsigned long long C[N][N];

int main() {

for(int i = 0; i < N; i++){

   for(int j = 0; j <= i; j++){

       if(j==i || j==0) C[j][i] = 1;

           else C[j][i] = C[j][i-1] + C[j-1][i-1];

       cout << C[j][i] << " ";

   }

   cout << endl;

}

return 0;

}

В дальнейшем придётся применять длинную арифметику, чтобы получать правильные ответы для достаточно больших значений N.

Задача №286.  Салаты (acmp.ru)

(Время: 1 сек. Память: 16 Мб)

Как-то раз, придя домой со школы, Света обнаружила записку от мамы, в которой она просила сделать салат. Света знала, что салат – это смесь двух или более ингредиентов, поэтому ей не составило труда выполнить мамину просьбу.

Но Света хочет стать математиком, поэтому, для тренировки, решила посчитать, сколько различных салатов она сможет сделать из имеющихся продуктов (майонез, огурцы, помидоры). После небольших расчетов она получила ответ: 4.

Зная, что вы любите интересные задачки, и хотите стать программистами, Света попросила вас написать программу, которая определяет количество различных салатов для произвольного числа ингредиентов.

Входные данные

Натуральное число N – количество имеющихся ингредиентов (N < 32).

Выходные данные

Одно число – количество различных салатов.

Примеры

№	Ввод	Вывод
1	3	4
2	4	11

Решение

Наверное самое неэффективное решение, которое можно придумать для такой задачи, состоит в том, чтобы пытаться перебирать все возможные подмножества из 1..N– множества всех ингредиентов.

Количество всех подмножеств из множества N элементов составляет 2^N. Это очень легко доказать, воспользовавшись правилом умножения. Для каждого элемента имеется два возможных выбора – включать его в подмножество или не включать.

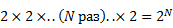
При этом салат, рассматривая его как подмножество (звучит ужасно, не правда ли), согласно условию задачи не может состоять из одного ингредиента – количество таких подмножеств равно N. И, естественно, он не может состоять из пустого множества ингредиентов. В итоге количество способов равно:

Для вычисления 2^N нет нужды пользоваться функцией возведения в степень или циклом. Достаточно применить побитовый сдвиг вправо на N разрядов.

#include <iostream>

intmain() {

int n;

std::cin >> n;

std::cout << (1 << n) – n - 1;

}

Задача №287.  Шахматные ладьи

Требуется найти число способов расставить на шахматной доске N×N K ладей так, чтобы они не били друг друга. Все ладьи считаются одинаковыми.

Входные данные

Во входном файле INPUT.TXT записаны натуральные числа N и K (N, K <= 20).

Выходные данные

В выходной файл OUTPUT.TXT выведите одно целое число – ответ на задачу.

Пример

INPUT.TXT	OUTPUT.TXT
8 8	40320

Решение

Самым неудачным решением будет использовать полный перебор всех вариантов с помощью рекурсии, как в случае с ферзями. Попробуем применить в задаче знание комбинаторики. Во-вторых, очевидно, что две мирные[41] ладьи не могут стоять на одной вертикали или горизонтали. Таким образом, каждая ладья должна стоять на отдельной вертикали, а для K ладей требуется K вертикалей. Расставить K ладей по K вертикалям высоты N существует  способов. Если Kбольше, чем N (ладей больше, чем вертикалей), то никакая расстановка не возможна. Во-вторых, выбрать K вертикалей из N можно 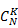 способами. Т.е. всего имеется

требуемых расстановок. Однако по этой формуле для больших величин n и k вычисление факториала может привести к переполнению. Преобразуем полученную формулу к виду:

или, что тоже самое

#include <fstream>

using namespace std;

int main() {

ifstream cin("input.txt");

ofstream cout("output.txt");

 unsigned long long s=1, i, n, k;

cin >> n >> k;

for (i = 1; i <= k; i++)

   (s *= (n-k+i)*(n-k+i)) /= i;

cout << (n<k ? 0 : s);

}

Примечание: в программе нельзя было использовать формулу в виде

s *= (n-k+i)*(n-k+i) / i;

несмотря на их математическую тождественность. В тех случаях, когда n-k+i не делится нацело на i, величина s будет домножаться на целую часть описанного выражения, что приведёт к неправильному ответу.

Задача №288.  Шаблоны (acmp.ru)

(Время: 1 сек. Память: 16 Мб)

Шаблоном размера n назовем строку длины n, каждый из символов которой входит в множество {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f, g, ?}. Шаблоны преобразуются в строки из цифр по следующим правилам:

· символы от 0 до 9 могут быть преобразованы только сами в себя;

· символ a может быть преобразован в любой из символов 0,1, 2, 3;

· символ b может быть преобразован в любой из символов 1,2,3,4;

· символ c может быть преобразован в любой из символов 2,3,4,5;

· символ d может быть преобразован в любой из символов 3,4,5,6;

· символ e может быть преобразован в любой из символов 4,5,6,7;

· символ f может быть преобразован в любой из символов 5,6,7,8;

· символ g может быть преобразован в любой из символов 6,7,8,9;

· символ ? может быть преобразован в любой из символов от 0 до 9;

Даны два шаблона: p1 и p2. Рассмотрим множество S1 строк, которые могут быть получены из p1 по описанным правилам, и множество S2 строк, которые могут быть получены из p2. Необходимо найти количество строк, входящих в оба этих множества.

Входные данные

Первая строка входного файла INPUT.TXT содержит шаблон p1, вторая — шаблон p2. Шаблоны имеют одинаковый положительный размер, не больше 9.

Выходные данные

В выходной файл OUTPUT.TXT выведите ответ на задачу.

Примеры

№	INPUT.TXT	OUTPUT.TXT
1	??? abc	64
2	??? 000	1
3	abc 999	0

Решение

Зададим в матрице T для каждого символа шаблона его нижнюю и верхнюю границу. Сами элементы шаблона сохраним в строке alphabet.

#include<fstream>

usingnamespacestd;

string alphabet = "0123456789abcdefg?", p1, p2;

int t[2][18]={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, 6, 0,

         0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 3, 4, 5, 6, 7, 8, 9, 9},

   count = 1, i, j, i1, i2;

int main(){

ifstream cin("input.txt");

ofstream cout("output.txt");

cin >> p1 >> p2;

int n = p1.size();

for(i = 0; i < n; i++){

   for(j = 0; j < 18; j++){

       if(p1[i] == alphabet[j]) i1=j;

       if(p2[i] == alphabet[j]) i2=j;

   }

   count *= min(t[1][i1],t[1][i2]) - max(t[0][i1],t[0][i2]) + 1;

   if (count <= 0) {cout << 0; return 0;}

}

cout << count;

}

Задача №289.  Нолики (acmp.ru)

(Время: 1 сек. Память: 16 Мб)

Для заданных натуральных чисел N и K требуется вычислить количество чисел от 1 до N, имеющих в двоичной записи ровно K нулей.

Например, если N=8 и K=1, то мы можем записать все числа от 1 до 8 в двоичной системе счисления:

1, 10, 11, 100, 101, 110, 111 и 1000.

Откуда видно, что только числа 10, 101 и 110 имеют ровно один ноль в записи, т.е. правильный ответ – 3.

Входные данные

В единственной строке вх записано два натуральных числа через пробел N и K, не превышающих 10⁹.

Выходные данные

Вывести одно целое число — количество чисел от 1 до N с K нулями в двоичном представлении.

Примеры

№	Ввод	Вывод
1	8  1	3
2	13  2	4
3	1000  5	210

Решение

 

#include <iostream>

using namespace std;

 

int n, k, c[32][32], l, ans, i, j, cnt0, a[32];

 

int main(){

for(i = 0; i < 32; i++)     // таблица сочетаний из i по j

   for(j = 0; j <= i; j++){

       c[i][j] = (!j || j == i ? 1 : c[i-1][j] + c[i-1][j-1]);

   }

   

cin >> n >> k;

   

if(k > 31){            // отсекаем заведомо невозможные k

   cout << 0;

   return 0;

}

   

while(n){              // получаем двоичное представление n

   a[l++] = n & 1;    // l - длина двоичного представления

   n >>= 1;

}

   

for(i = k + 1; i < l; i++) // проверяем числа, в двоичной записи

   ans += c[i-1][k];  // которых меньше l цифр

   

for (i = l - 2; ~i; i--){ // проверяем числа, у которых l цифр

   if(a[i]){          // в двоичной записи

       if (k-cnt0-1 >= 0)

           ans += c[i][k-cnt0-1];

   }

   else cnt0++;

}

if(cnt0 == k) ans++;

cout << ans;

}

Задача №290.  Делители числа N!

По заданному натуральному числу N необходимо вычислить количество натуральных чисел, которые являются делителями N! (факториала числа N).

Например, при N=4, N!=4·3·2·1=24. Это число имеет такие делители: 1, 2, 3, 4, 6, 8, 12, 24. Таким образом искомое количество равняется 8.

Входные данные

Входной файл содержит одно целое число N (1 ≤ N ≤ 45).

Выходные данные

Выходной файл должен содержать одно целое число - найденное количество делителей.

Пример

Ввод	Вывод
4	8

Решение

#include <iostream>

using namespace std;

// все простые числа до 50

const int prime[14] = {2, 3, 5, 7, 11, 13, 17,

                 19, 23, 29, 31, 37, 41, 43};

 

int main(){

int cnt[14] = {0,}; // массив счетчиков для простых делителей

long long k = 1;

int n, i, j, a;

cin >> n;

for (i = 2; i <= n; i++)

   for(j = 0, a = i; a > 1; j++)

       while(a % prime[j] == 0){

           a /= prime[j];

           ++cnt[j];

       }

for (i = 0; i < 14; i++)

   k *= cnt[i] + 1;

cout << k << endl;

return 0;

}

Задача №291.  Количество треугольников

Московская командная олимпиада 2005–2006 уч. г.

(Время: 1 сек. Память: 16 Мб)

Рассмотрим фигуру, аналогичную той, что на рисунке (большой равносторонний треугольник, составленный из маленьких равносторонних треугольников). На рисунке приведена фигура, состоящая из 4-х уровней треугольников.

Требуется написать программу, которая будет определять, сколько всего в ней треугольников (необходимо учитывать не только "маленькие" треугольники, а вообще все треугольники — в частности, треугольник, выделенный жирным, а также вся фигура, являются интересующими нас треугольниками).

Рис. 52. Иллюстрация к задаче "Количество треугольников"

Входные данные

Одно число N — количество уровней в фигуре (1 <= N <= 10⁵).

Выходные данные

Одно число - количество треугольников в такой фигуре.

Примеры

№	Ввод	Вывод
1	1	1
2	2	5
3	4	27

Решение

Заметим, что все возможные треугольники — равносторонние, и одна из их сторон — горизонтальная. Такие треугольники могут быть двух типов: горизонтальная сторона снизу (треугольник ориентирован как вся фигура) или горизонтальная сторона сверху (треугольник ориентирован как выделенный треугольник на рисунке из условия).

Подсчитаем сначала количество треугольников первого типа. Заметим, что каждый такой треугольник однозначно задается своим основанием, а значит, парой его концов — узлов сетки, лежащих на одной горизонтали. Если в некоторой горизонтали k узлов, то пару точек можно выбрать k(k – 1)/2 способами, то есть существуют k(k – 1)/2 треугольников с таким основанием. Если фигура состоит из n уровней, то в верхней горизонтали имеются 2 узла, в следующей — 3, …, в последней — n(n + 1)/2. Таким образом, количество треугольников первого типа равно

Для предложенных в задаче ограничений на входные данные можно вычислить эту сумму, используя цикл. Но можно вычислить эту сумму в явном виде, не используя компьютер.

Чуть сложнее подсчитать количество треугольников второго типа. Покажем один из возможных способов это сделать. Для удобства обозначим

Подсчитаем отдельно количество треугольников со стороной 1, со стороной 2, со стороной 3 и т.д. Из рисунка видно, что эти количества равны

S_n-1, S_n-3, S_n-5, … соответственно (слагаемые каждой из сумм S_i — это количества треугольников соответствующего размера в одном горизонтальном ряду).

Таким образом, общее количество треугольников второго типа равно

(последнее слагаемое в этой сумме равно S2 или S1 в зависимости от четности n). Эту сумму также можно сосчитать, используя цикл, а можно упростить, записав ответ в явном виде. Общее количество треугольников обоих типов равно

Доказать это можно по индукции [7].

Для первых 10⁵ натуральных чисел будет работать формула, полученная преобразованием формулы для четных n.

Результат целочисленного деления в этой формуле совпадёт как с результатом формулы для n=2k, так и для n=2k+1.

#include<iostream>

int main(){

__int64 n;

std::cin >> n;

std::cout << n*(n + 2)*(n * 2 + 1) / 8;

}