Анализ динамики безработицы с использованием временных рядов

 

1. Расчет аналитических (∆_у, Т_р, Т_пр, |%|) и средних показателей рядов динамики.

Наиболее простым показателем анализа динамики является абсолютный прирост (Dу): ,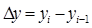

где: Dу - абсолютный прирост; у_i - текущий уровень ряда; у_{i - 1} - предшествующий уровень; i - номер уровня.

Цепные коэффициенты роста исчисляются по формуле:

 

где: К _р - коэффициент роста.

Базисные коэффициенты роста исчисляются:

 

Если коэффициенты роста выражаются в процентах, то их называют темпами роста: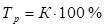   

Наряду с коэффициентами роста исчисляются и коэффициенты прироста:

 (по цепной системе),

 (по базисной системе).

Абсолютные и относительные величины необходимо брать вне отрыва друг от друга. Поэтому большое значение имеет расчет показателя абсолютного значения 1% прироста:

|%|=

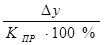
Средний абсолютный прирост определяется:

 (по цепной системе),

, (по базисной системе).

Средний коэффициент роста, а, следовательно, и прироста:  

Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах:  

 

Таблица 1. Расчетная таблица для ∆_у, Т_р, Т_пр,|%|.

год	безработные- всего, тыс.чел.	абсолютн прирост, тыс чел		темп роста, %		темп прироста, %		абс.знач. 1% прироста, тыс.чел.
		базис	цепн	базис	цепн	базис	цепн
1992	29,3	-	-	100	-	0	-	-
1993	29,25	-0,05	-0,05	99,83	99,83	-0,171	-0,171	0,29
1994	48,03	18,73	18,78	163,93	164,21	63,93	64,21	0,29
1995	60,06	30,76	12,03	204,98	125,05	104,98	25,05	0,48
1996	66,39	37,09	6,33	226,59	110,54	126,59	10,54	0,60
1997	96,26	66,96	29,87	328,53	144,99	228,53	44,99	0,66
1998	93,59	64,29	-2,67	319,42	97,23	219,42	-2,77	0,96
1999	84,74	55,44	-8,85	289,22	90,54	189,22	-9,46	0,94
2000	92,91	63,61	8,17	317,099	109,64	217,099	9,64	0,85
2001	81,26	51,96	-11,65	277,34	87,47	177,34	-12,54	0,93
2002	69,73	40,43	-11,53	237,99	85,81	137,99	-14,19	0,81
2003	76,85	47,55	7,12	262,29	110,21	162,29	10,21	0,697
2004	67,9	38,6	-8,95	231,74	88,35	131,74	-11,65	0,77
2005	54,13	24,83	-13,77	184,744	79,72	84,744	-20,28	0,68
итого	950,4	-	24,83	-	-	-	-	-

 

По данным таблицы 1 видно, что максимальное значение абсолютного прироста (по цепной системе) зафиксировано в 1997 году (29,87 тыс.чел.), минимальное значение - в 2005 году (-13,77тыс.чел.). Максимальное значение абсолютного прироста по базисной системе составило 66,96 тыс.чел. в 1997 году, минимальное - -0,05 тыс.чел. в 1993 году. В общем 1997г. по сравнению с 1992г. численность безработных увеличилась на 66,96 тыс.чел. и самая высокая численность безработных за период 1992-2005гг. зарегистрирована в 1997г - численность безработных в 3,28 раза больше, чем в 1992г. На 84,7% численность безработных в 2005г. больше, чем безработных в 1992г. 0,96 тыс.чел. приходится на 1% прироста безработных в 1998г.

Рассчитаем среднегодовой уровень численности безработных:

У=950,4/14=67,9тыс.ч., т.е. за период 1992-2005гг. ежегодно численность безработных составила 67,9 тыс. чел.

Средний абсолютный прирост:

Равен ∆=24,83/13=1,91тыс.чел., т.е. за период с 1992-2005гг. в среднем ежегодно абсолют. прирост численности безработных составил 1,91тыс. чел.

Средний темп роста:

Т_р=1,0096 или 100,96% - это говорит о том, что с 1992-2005гг. в среднем ежегодно темп роста безработных составил 100,96%.

Средний темп прироста:

Т_пр = 100,96%-100%= 0,96% - с 1992-2005гг. в среднем темп прироста достигал 0,96%.

2. Определение наличия тенденции средних и дисперсии на базе методов: Метод проверки существенности разности средних.

Выдвигаем гипотезу Н₀ об отсутствии тенденции, проверка осуществляется на основе кумулятивного t-критерия Стьюдента. Расчетное значение определяется по формуле:

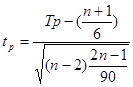, где  Таблица 2. Для расчёта характеристик S² и Z².

год	безработные-всего, тыс.чел.	S2	Z2
1992	29,3	1488,857	1488,857
1993	29,25	1492,72	2981,58
1994	48,03	394,25	3375,83
1995	60,06	61,24	3437,07
1996	66,39	2,237	3439,3
1997	96,26	805,1	4244,4
1998	93,59	660,71	4905,12
1999	84,74	284,07	5189,18
2000	92,91	626,22	5815,4
2001	81,26	178,87	5994,27
2002	69,73	3,4	5997,67
2003	76,85	80,36	6078,03
2004	67,9	0,000204	6078,03
2005	54,13	189,22	6267,25
итого	950,4	6267,25	65291,97
СРЕДН	67,886

 

 

T_p= 10,418; t_p=4,174

Табличное значение t-критерия Стьюдента для числа степеней свободы df=(n-2)=12 и вероятности 95% составляет 2,1788. Tp >t_табл → гипотеза Н₀ о равенстве средних отвергается, расхождение между средними существенно значимо и не случайно, то в ряде динамики существует тенденция средней и, следовательно в исходном временном ряду тенденция имеется.

Метод Фостера – Стюарта.

Кроме определения наличия тенденции явления этот метод позволяет выявить основную тенденцию дисперсии уровней ряда динамики.

1. Сравнивается каждый уровень ряда со всеми предыдущими, при этом

если у_i >y_i-1, то U_i=1; L_i=0; при у_i <y_i-1, то U_i=0; L_i=1;

2. Вычисляются значения величин S и d:

S=∑S_i , где S_i =U_i + L_i d=∑d_i , где d_i =U_i - L_i

Показатель S характеризует тенденцию изменения дисперсии ряда динамики, а показатель d - изменение тенденций в среднем.

3. Проверяется с использованием t-критерия Стьюдента гипотеза о том, можно ли считать случайными разности S-µ и d-0:

4. Сравниваются расчетные значения t_s и t_d c табличными значениями.

Таблица 3. Для определения U_i и L_i.

год	тыс.чел.	Ui	Li
1992	29,3	0	0
1993	29,25	1	0
1994	48,03	1	0
1995	60,06	1	0
1996	66,39	1	0
1997	96,26	1	0
1998	93,59	0	1
1999	84,74	0	1
2000	92,91	1	0
2001	81,26	0	1
2002	69,73	0	1
2003	76,85	1	0
2004	67,9	0	1
2005	54,13	0	1

 

 

 

 

Определяем значения S=13 и d=1. По данным таблицы при n=14, µ=4,636, σ₁=1,521, σ₂ =2,153. По этим значениям рассчитаем:

t_s =(13-4,636)/1,521=5,499 и t_d=(1-0)/2,153=0,465

Табличное значение t_табл для двустороннего критерия при уровне значимости 0,10 равно t_табл =1,761, т.е. t_табл > t_d , t_табл < t_s → гипотеза об отсутствии тенденции в дисперсии показателя численности безработных отвергается, а в средней - подтверждается.

3. Определение наличия тенденции автокорреляции.

Автокорреляцию измеряют при помощи коэффициента автокорреляции:

 , где

σ_я и σ_я+1-среднеквадратические отклонения рядов и 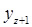соответственно.

Если значение последнего уровня (y_n) ряда мало отличается от первого (y₁), то сдвинутый ряд можно условно дополнить, принимая y_n=y₁. Тогда y_t=y_t+1 и значит формула коэффициента автокорреляции примет вид:

 

Таблица 4. Исходные данные и расчет необходимых величин.

год
	Числен-ть безраб-х тыс.чел.(yt)	уровни со сдвигом (yt+1)		yt2
1992	29,3	29,25	857,025	858,49
1993	29,25	48,03	1404,878	855,5625
1994	48,03	60,06	2884,682	2306,881
1995	60,06	66,39	3987,383	3607,204
1996	66,39	96,26	6390,701	4407,632
1997	96,26	93,59	9008,973	9265,988
1998	93,59	84,74	7930,817	8759,088
1999	84,74	92,91	7873,193	7180,868
2000	92,91	81,26	7549,867	8632,268
2001	81,26	69,73	5666,26	6603,188
2002	69,73	76,85	5358,751	4862,273
2003	76,85	67,9	5218,115	5905,923
2004	67,9	54,13	3675,427	4610,41
2005	54,13	29,3	1586,009	2930,057
итого	950,4	950,4	69392,08	70785,83
средн	67,89		4956,58	5056,13

 

r_a = 0,778

Приводим сопоставление полученного коэффициента автокорреляции с табличным при выборке n=14. При уровне значимости Р=0,05 r_{a табл} =0,335.

Следовательно, r_{a факт} > r_{a табл} , что говорит о наличии автокорреляции в ряду динамики.

Критерий Дарбина - Уотсона.

Выдвигается гипотеза Н₀ об отсутствии автокорреляции.

 

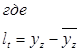
Таблица 5. Для определения величины Дарбина-Уотсона.

год	тыс.чел.	t	t2	yt	ytˆ	lt	Lt+1	Lt2	Lt+1-lt	(Lt+1-lt)2
1992	29,3	-13	169	-380,9	51,77	-22,47	-25	504,9	-2,53	6,4
1993	29,25	-11	121	-321,75	54,25	-25	-8,7	625	16,3	265,69
1994	48,03	-9	81	-432,27	56,73	-8,7	0,85	75,69	9,55	91,2
1995	60,06	-7	49	-420,42	59,21	0,85	4,7	0,72	3,85	14,82
1996	66,39	-5	25	-331,95	61,69	4,7	32,09	22,09	27,39	750,21
1997	96,26	-3	9	-288,78	64,17	32,09	26,94	829,8	-5,15	26,52
1998	93,59	-1	1	-93,59	66,65	26,94	15,61	125,76	-11,33	128,37
1999	84,74	1	1	84,74	69,13	15,61	21,3	243,67	5,69	32,38
2000	92,91	3	9	278,73	71,61	21,3	7,17	453,69	-14,13	199,66
2001	81,26	5	25	406,3	74,09	7,17	-6,84	51,41	-14,01	196,28
2002	69,73	7	49	488,11	76,57	-6,84	-2,2	46,79	4,64	21,53
2003	76,85	9	81	691,65	79,05	-2,2	-13,63	4,84	-11,43	230,65
2004	67,9	11	121	746,9	81,53	-13,63	29,88	185,78	43,51	1893,12
2005	54,13	13	169	703,69	84,01	-29,88	-	592,814	-	-
итого	950,4	-	910	1130,5	-	-	-	3756,83	-	5862,9

 

Величина критерия Дарбина – Уотсона D=5862,9/3756,83=1,56

d_L =1,08

d_U =1,36

Расчитанное значение попадает в отрезок от d_U до 4-d_U. Следовательно, нет оснований отклонять гипотезу Н₀ об отсутствии автокорреляции в остатках.

После того как установлено наличие тенденции в ряду динамики, производится ее описание с помощью методов сглаживания.

4. Выявление основной тенденции.

Метод скользящей средней.

Сначала найдем скользящие средние путем суммирования уровней ряда за каждые 4 года и разделив полученные суммы на 4. Потом найдем центрированные скользящие средние, для чего найдем средние значения из 2 последовательных скользящих средних. И найдем оценки сезонной компоненты.

 

Таблица 6. Расчет оценок сезонной компоненты.

	Безраб-ных, тыс.чел.	Скольз. Средняя	Центр. Скол.сред	Оценка сезон комп S
1	48,03	-	-	-
2	60,06	67,685	-	-
3	66,39	79,075	73,38	-6,99
4	96,26	85,245	82,16	14,1
5	93,59	91,875	88,56	5,03
6	84,74	88,125	90	-5,26
7	92,91	82,16	85,143	7,7675
8	81,26	80,188	81,173	0,086
9	69,73	73,935	77,061	-7,331
10	76,85	67,153	70,544	6,306
11	67,9	-	-	-
12	54,13	-	-	-

 

Рис. 1. Динамика численности безработных за 1994-2005гг.

 

Скользящая средняя дает более или менее плавное изменение уровней.

На графике не проявляется сильно выраженный недостаток скользящих средних. Но в начале и в конце динамического ряда отсутствуют данные, в результате чего становится не совсем ясна закономерность. Это и является минусом данного, наиболее простого из всех остальных метода. Для более точного анализа использую метод аналитического выравнивания.

Метод аналитического выравнивания и определение параметров.

Аналитическое выравнивание ряда динамики имеет задачу найти плановую линию развития (тренд) данного явления, характеризующую основную тенденцию её динамики.

Для отображения основной тенденции развития явления применяются полиномы разной степени, при которых оценка параметров производится по МНК. Так, для линейного тренда y=a+bt система уравнений следующая:

 

Таблица 7. Расчет параметров линейного тренда.

год	тыс.чел.	t	t2	уt
1992	29,3	1	1	29,3
1993	29,25	2	4	58,5
1994	48,03	3	9	144,09
1995	60,06	4	16	240,24
1996	66,39	5	25	331,95
1997	96,26	6	36	577,56
1998	93,59	7	49	655,13
1999	84,74	8	64	677,92
2000	92,91	9	81	836,19
2001	81,26	10	100	812,6
2002	69,73	11	121	767,03
2003	76,85	12	144	922,2
2004	67,9	13	169	882,7
2005	54,13	14	196	757,82
итого	950,4	105	1015	7693,23

 

Из таблицы 7 подставим значения в систему и получим:

Уравнение "линейной" модели примет вид: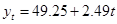  

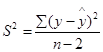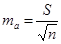Оценим параметры уравнения на типичность. Для расчёта используем следующие формулы:

где: S²- остаточная уточнённая дисперсия; m_а, m_в- ошибки по параметрам.

После подстановки значений получились следующие данные:

Оценим значимость параметров модели по критерию Стьюдента. Предположим, что параметры и коэффициент корреляции стат. значимы.

где: t_a , t_b- расчётное значение t-критерия Стьюдента для параметров.

После подстановки данных в формулы получим следующие значения:

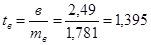
Сравним полученное значение с табличным t_{табличное} при Р=0,05 (уровень значимости) и (n-2)= 2,1788. Так как t_{расчётное} > t_{табличное} , то параметры уравнения типичны (значимы) и данное уравнение используется в дальнейших расчетах.

Оценим уравнение в целом по критерию Фишера, выдвигаем гипотезу Н₀: о том, что коэффициент регрессии равен нулю.

Fф=D_факт/D_ост=2410,54/405,25=5,95.

F_T(v₁=1;v₂=12)=4,75.

Поскольку Fф > F_T при 5%-ном уровне значимости гипотеза Н₀ отвергается, уравнение в целом стат. значимо.

Из уравнения видно, что ежегодно численность безработных возрастала в среднем на 2,49%.

Построим график исходных данных.

 

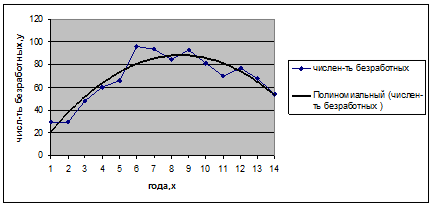
Рис. 2. График исходных данных.

 

По графику видно, что временной ряд характеризуется сначала тенденцией возрастания до 2000г., а затем убывания. Можно предположить, что данный ряд, вероятно, развивается согласно полиномиальной функции, которая описывается параболой второго порядка:

Система нормальных уравнений для расчета параметров параболы 2-ой степени составит:

год	тыс.чел.	t	t2	t3	t4	yt	yt2
1992	29,3	1	1	1	1	29,3	29,3
1993	29,25	2	4	8	16	58,5	117
1994	48,03	3	9	27	81	144,09	432,27
1995	60,06	4	16	64	256	240,24	960,96
1996	66,39	5	25	125	625	331,95	1659,75
1997	96,26	6	36	216	1296	577,56	3465,36
1998	93,59	7	49	343	2401	655,13	4585,91
1999	84,74	8	64	512	4096	677,92	5423,36
2000	92,91	9	81	729	6561	836,19	7525,71
2001	81,26	10	100	1000	10000	812,6	8126
2002	69,73	11	121	1331	14641	767,03	8437,33
2003	76,85	12	144	1728	20736	922,2	11066,4
2004	67,9	13	169	2197	28561	882,7	11475,1
2005	54,13	14	196	2744	38416	757,82	10609,5
итого	950,4	105	1015	11025	127687	7693,23	73913,9

Решив систему, получим параметры уравнения тренда:

а=13,37; b=13,94; c=-1,0017.

Соответственно уравнение тренда составит: у =13,37+13,94t-1,0017t²

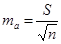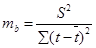Оценим параметры уравнения на типичность.

где: S²- остаточная уточнённая дисперсия; m_а, m_в, m_r - ошибки по параметрам.

После подстановки значений получились следующие данные:

 

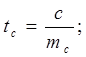Оценим значимость параметров модели по критерию Стьюдента.

 

Предположим, что параметры и коэффициент корреляции стат.

 

значимы. Для расчёта использую следующие формулы:

где: t_a , t_b , t_r - расчётное значение t-критерия Стьюдента для параметров.

После подстановки данных в формулы получил следующие значения:

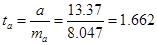
Сравним полученное значение с табличным t-критерием Стьюдента. t_{табличное} при Р=0,05 и (n-2)= 2,1788. Так как t_{расчётное} > t_{табличное} , то параметры b и r уравнения типичны (значимы). Так как t_{расчётное} < t_{табличное} , то параметры с и а незначимы.

Оценим уравнение в целом по критерию Фишера, выдвигаем гипотезу Н₀:о том, что коэффициент регрессии равен нулю.

Fф=D_факт/D_ост=10333,6/906,597=11,398.

F_T(v₁=1;v₂=12)=4,75.

Т.к. Fф > F_T при 5%-ном уровне значимости гипотеза Н₀ отвергается, уравнение в целом стат. значимо.

5. Автокорреляция уровней временного ряда.

Для выбора прогностической модели необходимо исследовать автокорреляцию уровней динамического ряда, т.е. изучить корреляционную связь между последовательными значениями уровней временного ряда.

 

Таблица 9. Расчет коэффициента автокорреляции.

год	тыс.чел.	yt-1	yt-2	yt-3
1992	29,3	-	-	-
1993	29,25	29,3	-	-
1994	48,03	29,25	29,3	-
1995	60,06	48,03	29,25	29,3
1996	66,39	60,06	48,03	29,25
1997	96,26	66,39	60,06	48,03
1998	93,59	96,26	66,39	60,06
1999	84,74	93,59	96,26	66,39
2000	92,91	84,74	93,59	96,26
2001	81,26	92,91	84,74	93,59
2002	69,73	81,26	92,91	84,74
2003	76,85	69,73	81,26	92,91
2004	67,9	76,85	69,73	81,26
2005	54,13	67,9	76,85	69,73
итого	950,4	896,27	828,37	751,52

 

По данному ряду определяю серию коэффициентов автокорреляции (автокорреляционную функцию):

r_a1=0,809, r_a2=0,52, r_a3=0,233, r_a4=-0,421, r_a5=-0,854, r_a6=-0,746, r_a7=-0,894, r_a8=-0,907, r_a9=-0,735, r_a10=-0,898, r_a11=-0,919.

Построим график автокорреляционной функции.

 

Рис. 3. Коррелограмма для ряда численности безработных в РБ за 1992-2005гг.

 

Коррелограмма представляет собой затухающую функцию. По графику видно, что наиболее высоким оказался r_a1=0,809, т.е. уровни текущего года на 80,9% обусловлены уровнями предыдущего года. Поэтому ряд содержит только тенденцию и не содержит периодических колебаний. В данном ряду отсутствует трендовая компонента Т и циклическая (сезонная) компонента S.