 |
Главная |
Векторная алгебра и аналитическая геометрия.
|
из
5.00
|
Методические указания к выполнению контрольных работ по математике
для студентов 1 курса, обучающихся
по заочной форме обучения
Москва 2019
| Оглавление
ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ 6 | ||
| I. Векторы на плоскости 6 | ||
| Нахождение координат вектора 6 | ||
| Длина вектора 6 Нахождение координат середины отрезка 7 Скалярное произведение векторов 7 Угол между векторами 8 Проекция одного вектора на другой вектор 8 | ||
| II. Прямая на плоскости 8 | ||
| Общее уравнение прямой 8 | ||
| Уравнение прямой проходящей через точку и перпендикулярной вектору 9 | ||
| Уравнение прямой проходящей через две точки 9 Каноническое уравнение прямой (уравнение прямой проходящей через точку и параллельной вектору) 9 Уравнение прямой в отрезках 10 Параметрическое уравнение прямой 10 Нормальное уравнение прямой 10 Расстояние от точки до прямой 11 | ||
| III. Векторы в пространстве 11 | ||
| Нахождение вектора 11 Длина вектора 11 Нахождение координат середины отрезка 12 Скалярное произведение векторов 12 Угол между векторами 13 Проекция одного вектора на другой вектор 13 Векторное произведение векторов 13 Смешанное произведение векторов 14 | ||
| IV. Плоскость в пространстве 14 | ||
| Общее уравнение плоскости 14 Уравнение плоскости проходящей через точку и перпендикулярной вектору 15 Уравнение плоскости, проходящей через три точки 15 Уравнение плоскости в отрезках 15 Нормальное уравнение плоскости 16 Расстояние от точки до плоскости 16 | ||
| V. Прямая в пространстве 17 Уравнение прямой проходящей через две точки 17 Каноническое уравнение прямой 17 Параметрическое уравнение прямой 18 Уравнение прямой, как пересечение двух плоскостей 18
VI. Кривые второго порядка на плоскости 19 Уравнение второй степени относительно двух переменных 20 Окружность (A C > 0, A = C) 20 Эллипс (A C > 0, A ≠ C) 20 Гипербола 22 Парабола 24
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ 48 | ||
|
| ||
Векторная алгебра и аналитическая геометрия на плоскости и в пространстве
I. Векторы на плоскости
Нахождение координат вектора
Пусть вектор задан двумя точками: 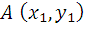 и
и 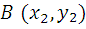
тогда координаты вектора 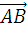 находятся по формуле:
находятся по формуле:
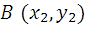 1.1
1.1 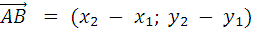
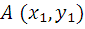
|
То есть из конца вектора (координаты точки 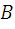 ) вычитается начало вектора (координаты точки
) вычитается начало вектора (координаты точки 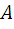 ) с координатами
) с координатами 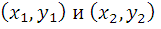 соответственно.
соответственно.
Длина вектора
a) если вектор 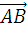 задан двумя точками
задан двумя точками  и
и  с координатами
с координатами 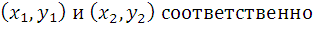 , то длина вектора
, то длина вектора 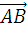 находится по формуле:
находится по формуле:
1. 2 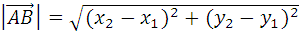
|
б ) если вектор 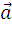 задан координатами
задан координатами 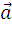 = (a 1 , a 2), то длину вектора
= (a 1 , a 2), то длину вектора 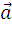 можно найти по формуле:
можно найти по формуле:
1.3 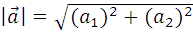
|
Нахождение координат середины отрезка
Если точка 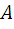 имеет координаты (x a , ya ), а точка B (x b , yb ), то координаты середины отрезка АB можно найти по формулам:
имеет координаты (x a , ya ), а точка B (x b , yb ), то координаты середины отрезка АB можно найти по формулам:
B
1.4 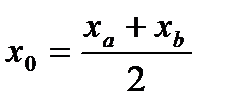 ' ' 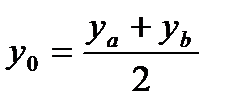 0
А 0
А
|
где точка О середина отрезка АВ, то есть 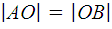 , иимеет координаты (x0 , y 0 ).
, иимеет координаты (x0 , y 0 ).
Скалярное произведение векторов
Если вектор 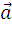 задан координатами (x 1 ; y 1), а вектор
задан координатами (x 1 ; y 1), а вектор 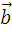 - (x 2 ; y 2), то скалярное произведение векторов находим по формуле:
- (x 2 ; y 2), то скалярное произведение векторов находим по формуле:
1.5 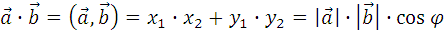
|
где φ – угол между векторами > 
Угол между векторами
Пусть заданы два вектора 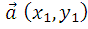 и
и 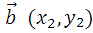 , тогда угол между векторами можно получить по формуле:
, тогда угол между векторами можно получить по формуле:
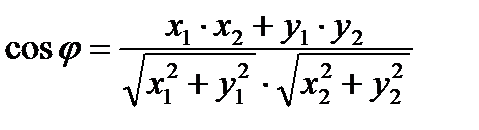
|
где 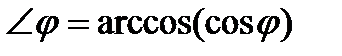 .
.
Формула 1.6 является следствием формул 1.5 и 1.3
Проекция одного вектора на другой вектор
Пусть вектор 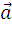 задан координатами (x 1 ; y 1), а вектор
задан координатами (x 1 ; y 1), а вектор 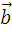 - (x 2 ; y 2), тогда проекцией вектора
- (x 2 ; y 2), тогда проекцией вектора 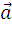 на вектор
на вектор 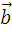 называется отрезок, который можно найти по формуле:
называется отрезок, который можно найти по формуле:
1.7 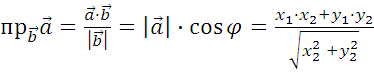
|
II. Прямая на плоскости
Общее уравнение прямой
2.1 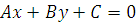  (А, В) (А, В)
|
Вектор 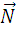 с координатами (А,В) – нормальный вектор, т. е. вектор перпендикулярный данной прямой.
с координатами (А,В) – нормальный вектор, т. е. вектор перпендикулярный данной прямой.
Уравнение прямой, проходящей через точку и перпендикулярной вектору
N (А,В)
2.2 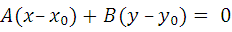 M0(x0,y0)
M0(x0,y0)
|
где 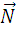 (А;В) – вектор нормали, или по другому нормальный вектор, M0(x0,y0) – точка лежащая на прямой, а (x,y) – координаты любой точки лежащей на данной прямой.
(А;В) – вектор нормали, или по другому нормальный вектор, M0(x0,y0) – точка лежащая на прямой, а (x,y) – координаты любой точки лежащей на данной прямой.
Уравнение прямой проходящей через две точки
Пусть заданы две точки M0(x0,y0) и M1(x 1 , y 1), тогда
M1(x1,y1)
2.3 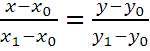 M0(x0,y0)
M0(x0,y0)
|
где (x , y)-координаты любой точки, лежащей на прямой
Каноническое уравнение прямой
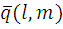 2.4
2.4 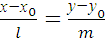 Мо(х0,у0)
Мо(х0,у0)
|
Уравнение прямой в отрезках
Если прямая не проходит через начало координат, то ее можно записать в виде:
У
2.5 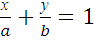 a х
b a х
b
|
прямая отсекает от осей координат прямоугольный треугольник с катетами a и b, где знак величин a и b показывает в какой четверти находится треугольник. Например, на рисунке 2.5: a >0, b<0 отсеченный треугольник находится в четвертый четверти.
Параметрическое уравнение прямой
На прямой за начало отсчета выберем точку M0(x0,y0), t-параметр, единица деления шкалированной прямой.
2.6 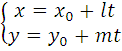 1
0 1
0
|
где 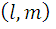 координаты направляющего вектора
координаты направляющего вектора 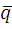
Нормальное уравнение прямой
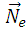 2.7
2.7 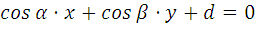
|
где 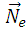 – единичный вектор нормали, то есть
– единичный вектор нормали, то есть
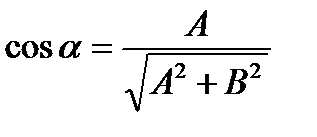 ,
, 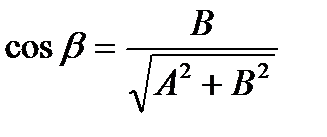 , а
, а 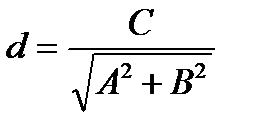 - расстояние от начала координат до заданной прямой.
- расстояние от начала координат до заданной прямой.
α, β - углы между вектором нормали и осями координат
Расстояние от точки до прямой
2.8 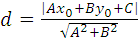 Мо(х0,у0) d Мо(х0,у0) d
|
III. Векторы в пространстве
Нахождение вектора
Пусть вектор задан двумя точками: А (х1, у1, z 1) и В (х2, у2, z 2)
Тогда координаты вектора 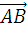 можно найти по формуле:
можно найти по формуле:
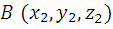 3.1
3.1 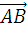 = (х2 - х1; у2 - у1; z 2 - z 1) = (х2 - х1; у2 - у1; z 2 - z 1)
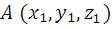
|
Длина вектора
а) если вектор 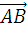 задан двумя точками: А (х1, у1,z1) и В (х2, у2,z2) Тогда длину вектора
задан двумя точками: А (х1, у1,z1) и В (х2, у2,z2) Тогда длину вектора 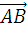 можно найти по формуле:
можно найти по формуле:
3.2 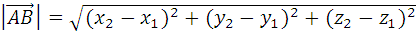
|
б) если вектор 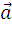 задан координатами
задан координатами 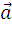 = (a 1 , a 2 , a 3), то длину вектора
= (a 1 , a 2 , a 3), то длину вектора 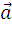 можно найти по формуле:
можно найти по формуле:
3.3 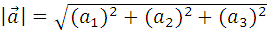
|
Нахождение координат середины отрезка
Если точка A имеет координаты 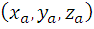 , а точка B -
, а точка B - 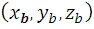 , то координаты середины отрезка АB можно найти по формулам:
, то координаты середины отрезка АB можно найти по формулам:
3.4 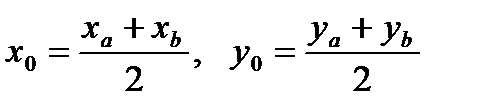 , , 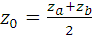 B
А О B
А О
|
Скалярное произведение векторов
Если вектор 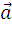 задан координатами (x 1 ; y 1
задан координатами (x 1 ; y 1 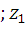 ), а вектор
), а вектор 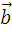 - (x 2 ; y 2
- (x 2 ; y 2 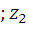 ), то скалярное произведение векторов находим по формуле:
), то скалярное произведение векторов находим по формуле:
3.5 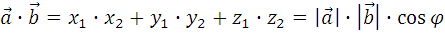
|
Угол между векторами
Пусть заданы два вектора 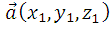 и
и 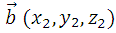
тогда угол между векторами можно получить по формуле:
3.6 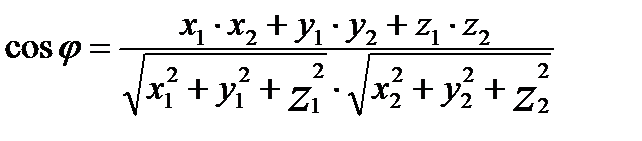
|
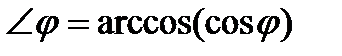
Проекция одного вектора на другой вектор
3.7 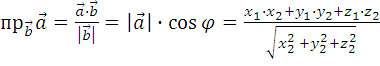
|
Векторное произведение векторов
Даны два вектора a и b.
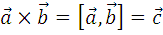
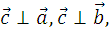
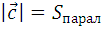
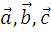 - образуют правую тройку векторов
- образуют правую тройку векторов
Буквой X или квадратными скобками обозначается векторное произведение двух векторов. Результатом такого произведения является вектор c, который перпендикулярен обоим заданным векторам ( a и b ). Кроме этого, длина полученного вектора численно равна площади параллелограмма, построенного на заданных векторах ( a и b ).
Координаты векторного произведения (вектора с) можно вычислить по формуле:
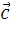 3.8
3.8  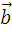
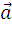
|
Смешанное произведение векторов
3.9 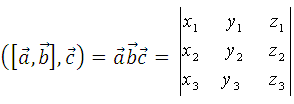
|
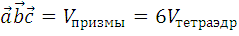
IV. Плоскость в пространстве
Общее уравнение плоскости
| N (А,В,С) 4.1 Ax + By + C z + D = 0 |
где A, B, C, D – координаты вектора нормали, причем хотя бы одно из чисел A, B, С отлично от нуля, (x;y;z) - координаты любой точки на плоскости.
Уравнение плоскости проходящей через точку и перпендикулярной вектору
4.2 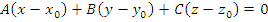 M0 (x0,y0,z0)
M0 (x0,y0,z0)
|
Уравнение плоскости, проходящей через три точки
M0 (x0,y0,z0), M1 (x1,y1,z1), M2 (x2,y2,z2)
M1 (x1,y1,z1)
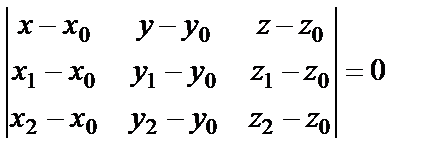
M2 (x2,y2,z2)
|
Уравнение плоскости в отрезках
Если плоскость не проходит через начало координат, то ее уравнение можно представить в следующем виде:
z
c
4.4 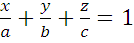 b
y
a
x b
y
a
x
|
Нормальное уравнение плоскости
 4.5
4.5 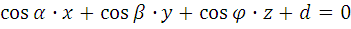
|
где 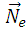 – нормальный единичный вектор с координатами:
– нормальный единичный вектор с координатами:
(  ,
, 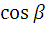 ,
, 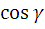 ), где
), где
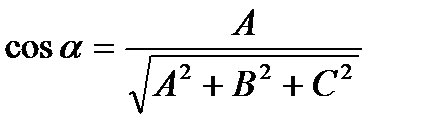 ,
, 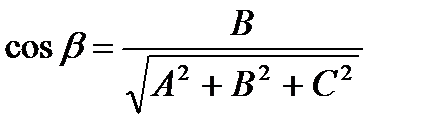 ,
, 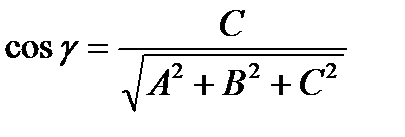 ,
, 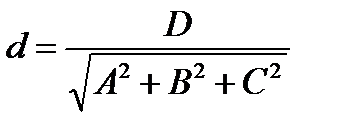
Расстояние от точки до плоскости
Пусть задано уравнение плоскости Ax + By + Cz + D =0 и точка 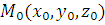 не лежащая на данной плоскости. Тогда расстояние от точки до плоскости находится по формуле
не лежащая на данной плоскости. Тогда расстояние от точки до плоскости находится по формуле
4.6 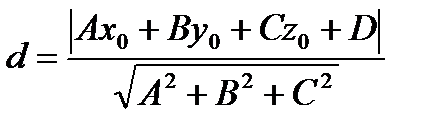
|
V. Прямая в пространстве
Прямая в пространстве характеризуется точкой на прямой и вектором, параллельным прямой, т.е. направляющим вектором. Направляющий вектор, если он не задан явно, можно получить с применением формул. Ниже приведены некоторые виды прямой в пространстве.
Уравнение прямой проходящей через две точки
Пусть заданы две точки M0(x0,y0) и M1(x 1 , y 1), тогда
M 1 ( x 1 , y 1 , z 1 )
5.1 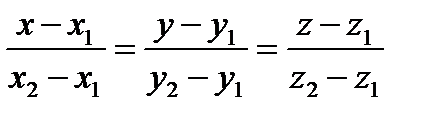 M 2 (x2,y2,z2)
M 2 (x2,y2,z2)
|
где (x , y , z) - координаты любой точки, лежащей на прямой
Каноническое у равнение прямой
q( l ,m, n )
5.2 L : 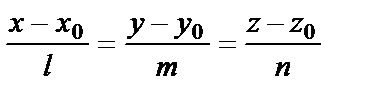 Мо(х0;у0; z 0 )
Мо(х0;у0; z 0 )
|
где, M 0 ( x 0 ; y 0 ; z 0 ) – лежащая точка на прямой L .
( l , m, n) – координаты направляющего вектора q прямой L.
Параметрическое уравнение прямой
На прямой за начало отсчета выберем точку M0(x 0 ; y 0 ; z 0), t-параметр, единица деления шкалированной прямой.
1
5.3 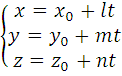 0
Мо(х0;у0; z 0 ) 0
Мо(х0;у0; z 0 )
|
где ( l , m, n) координаты направляющего вектора 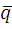
Уравнение прямой, как пересечение двух плоскостей
5.4 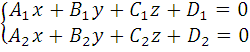
|
|
из
5.00
|
Обсуждение в статье: Векторная алгебра и аналитическая геометрия. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

