 |
Главная |
Уравнение точки имеет следующий вид
|
из
5.00
|

Гипербола (A C < 0, A ≠ C)
Гиперболой называется геометрическое место точек, разность расстояний от которых до двух данных точек (фокусов) есть постоянная величина 2а, причем 2а < 2 c, где 2с – расстояние между фокусами.
Каноническое уравнение гиперболы, симметричной относительно осей координат, имеет вид

|
где b2 = c2 – a2.
Параметр а называется вещественной полуосью гиперболы и представляет собой расстояние от начала координат до вершины гиперболы, параметр b называется мнимой полуосью.
Эксцентриситетом гиперболы называется величина
Расстояния текущей точки М (х,у) гиперболы до фокусов (фокальные радиусы) определяются по формулам
r 1 = 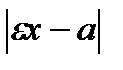
 r 2 =
r 2 = 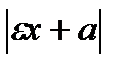
Прямые, заданные уравнениями y =  , являются асимптотами гиперболы.
, являются асимптотами гиперболы.
Гиперболаможет иметь другой вид, также симметричный относительно осей координат, имеет вид 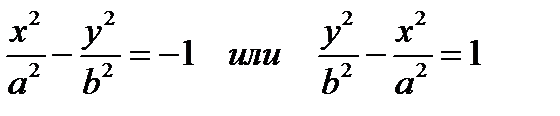
где b 2 = c 2 – a 2.
Параметр а называется вещественной полуосью гиперболы и представляет собой расстояние от начала координат до вершины гиперболы, параметр b называется мнимой полуосью.
2 прямые образуются в случае 
Парабола (A C = 0)
Параболой называется геометрическое место точек, одинаково удаленных от данной точки (фокуса) и данной прямой (директрисы).
Каноническое уравнение параболы, проходящей через начало координат и симметричной относительно оси Ох, имеет вид
|
Уравнение вида
x 2 = 2 py
|
описывает параболу, симметричную относительно оси Оу.
Фокальный радиус точки М(х,у), т.е. ее расстояние до фокуса на оси Ох, находится по формуле
r = x + 
Парабола, ось которой параллельна оси Оу, описывается уравнением y = ax 2 + bx + c .
Простая парабола относительно оси Оу
Смещенная парабола относительно оси Оу
Простая парабола относительно оси О x
Смещенная парабола относительно оси О x
Решение задач контрольной работы №2
Задача №1.
Даны координаты вершин треугольника АВС, A( ), B( ), C( ). Найти:
а) длину стороны АВ;
б) уравнение высоты, проведенной через вершину С;
в) уравнение медианы, проведенной через вершину С;
г) точку пересечения высот треугольника;
д) внутренний угол А в радианах;
е) длину высоты, опущенной из вершины В.
Решение задачи №1 а.
По условию задачи вершина треугольника имеют координаты A (0,-5), B (5,1), C (2,-2). Отметим данные точки на системе координат и нарисуем сторону АВ треугольника ABC.
(Смотри формулу 1.1)
Координаты вектора AB составят 
Найдем длину этого вектора (Смотри формулу 1.3)

Длина вектора АВ это то же самое, что и длина стороны АВ
Ответ: длина стороны АВ равна 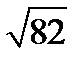
Решение задачи №1 б.
Найдем уравнение высоты, проведенной через вершину С;
Уравнение высоты это уравнение прямой перпендикулярной стороне АВ.
Следовательно, во-первых, необходимо найти уравнение стороны АВ
1)Таким образом, найдем уравнение стороны АВ.
Для этого есть две точки А и В.
Найдем уравнение стороны AB, как уравнение прямой проходящей через 2 точки A и B.
(Смотри формулу 2.3)
За первую точку  возьмем точку А, за вторую точку
возьмем точку А, за вторую точку  возьмем точку В.
возьмем точку В.
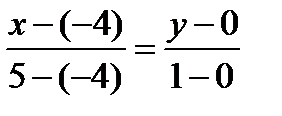

 , т.е. x - 9y + 4 = 0
, т.е. x - 9y + 4 = 0
2) Прямая СD перпендикулярна прямой АВ т. к прямая АВ задана каноническим уравнением: (Смотри формулу 2.4.),
Т.е.  , Вектор(9:1) параллельны прямой AB.
, Вектор(9:1) параллельны прямой AB.

Этот вектор q параллелен прямой AB и перпендикулярно прямой CD ,следовательно этот вектор можно принять за вектор перпендикулярный прямой CD, то есть нормальный вектор.
Таким образом для прямой CD есть т.С(2;-2) и вектор N=q=(9;1)
По формуле: 
Подставляем наши значения, получаем уравнение прямой CD

Упростив, получим


Ответ: 
Найдем уравнение медианы, проведенной через вершину С.
1)Найдем точку О, как середину отрезка АВ по формуле: (Смотри формулу 1.4)
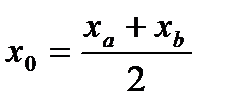 '
' 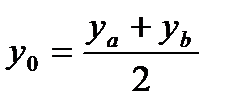
Так как А (-4;0), В (5;1)
Подставляем точки А (-4;0), В (5;1) в формулу 1.4 , получим:

2)Найдем уравнение медианы (прямой OC), как уравнение прямой проходящей через две точки О и С.
Уравнение медианы СО найдем, используя формулу для уравнения прямой, проходящей через две заданные точки.(Смотри формулу 2.4.) Медиана СО проходит через точки С(2;-2) и O (0,5;0,5), поэтому:

Ответ: 
Решение задачи №1 г.
Найти точку пересечения высот треугольника
1) Уравнение высоты CD найдено (задание №1б)
Имеем:

2)Аналогично получим уравнение высоты опущенной из т. В
Уравнение высоты BM - это уравнение прямой перпендикулярной стороне АC.
Таким образом, для начала найдем уравнение стороны для этого есть две точки А и С. (Смотри формулу 2.3.)
За первую точку возьмем точку А, за вторую возьмем точку С.


 или
или

Прямая ВМ перпендикулярна полученной стороне АС, следовательно, вектор нормали прямой АС (1;3), (коэффициенты при x и y) параллелен искомой прямой - высоте ВМ.
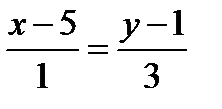

3)Найдем точку пересечения высоты т.К.
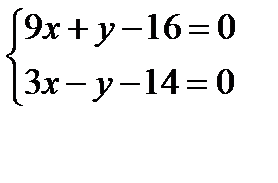
Сложив два уравнения, получим 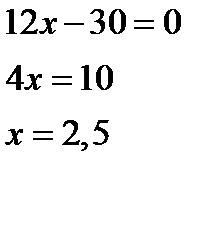
Подставив во второе уравнение x=2,5, получим 7,5-у-14=0
У=-6,5
Ответ: К(2,5;-6,5)
Решение задачи №1 д.
Найти внутренний угол A в радианах.
Для нахождения угла А в радианах, в начале найдем  .
.
 равен
равен  угла между векторами АВ и ВС. Вектор АВ
угла между векторами АВ и ВС. Вектор АВ
Найдем в задании №1а

Найдем вектор. (Смотри формулу 1.1) 

Найдем длину этого вектора
(Смотри формулу1.2 )

Угол между векторами находится (Смотри формулу1.6)

Ответ: А = 0,43 рад.
Решение задачи №1 е.
Длину высоты, опущенной из вершины В
Длина высоты ВМ находится, как расстояние из т.В до прямой АС
Уравнение прямой АС найдено в пункте 1г: x+3y+4=0
Найдем BM (Смотри формулу2.8), где за точку M0 принимаем точку B.
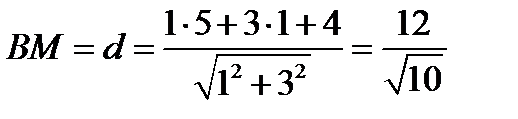
Ответ: BM = 
Задача №2.
Привести уравнение кривой второго порядка к каноническому виду и построить эту кривую.

Исходные данные 

Скомпонуем x и y
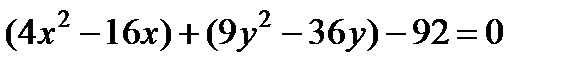
Вынесем коэффициенты х за скобки:


Приведем подобные члены:

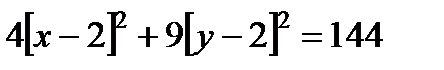
Разделим на 144

Ответ. 
Задача №3.
Найти координаты вектора  , перпендикулярного векторам
, перпендикулярного векторам  и
и  , если:
, если:
Задача №4.
Известно, что угол между векторами  и
и  равен
равен  . Найти косинус угла между векторами
. Найти косинус угла между векторами  и
и  .
.
Задача №5.
Даны координаты вершин пирамиды 

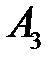
 .
.
Найти:
1) длину ребер  ,
,  ,
,  ;
;
2) угол между ребрами 
 и
и 
 ;
;
3) площадь грани 

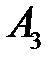 ;
;
4) проекцию вектора 
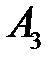 на вектор
на вектор 
 ;
;
5) объем пирамиды.
Решение задачи №5.1
Даны точки А1 (-1;0;2) А2 (3;2;5) А3 (7;0;-1) А4(-4;1;2)
Найти длину ребра А1 А2, А1А3, А1 А4 (Смотри формулу 3.3)
Найдем векторы А1 А2, А1 А3, А1 А4 (Смотри формулу 3.1, 3.3)



Решение задачи №5.2
Найти угол между ребрами А1 А2 и А1 А4
Угол между ребрами есть угол между векторами А1 А2 и А1 А4, координаты которых найдены в решении задания 5.1.
(Смотри формулу 3.6)

Решение задачи №5.3
Найдем площадь грани А1 А2 А3
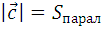

Решение задачи №5.4
Проекция вектора А1 А3 на вектор А1 А4 воспроизводится по формуле (3.7)
 Роль вектора А играет вектор А1 А3,а вектора В играет вектор А1 А4
Роль вектора А играет вектор А1 А3,а вектора В играет вектор А1 А4 
Решение задачи №5.5
Объем пирамиды вычисляется по формуле (Смотри формулу 3.9)
Вычислить объем тетраэдра с вершинами в точках 
 и его высоту, опущенную
и его высоту, опущенную  из вершины
из вершины  на грань
на грань 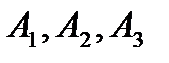 .
.

Решение. Найдем векторы:

Объем тетраэдра равен одной шестой от объема V параллелепипеда, построенного на векторах  .
.

отсюда V тетраэдра = 6 (куб. ед.).
Найдем теперь площадь S грани 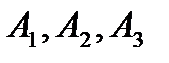 .
.
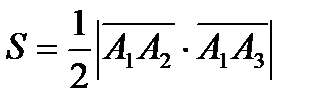 .
.
Найдем вектор производственных векторов  и
и 

Найдем длину полученного вектора:
 ,
,
отсюда  (кв.ед.), а
(кв.ед.), а  , т.к. HS есть объем треугольной призмы, равной половине объема V, т.е. 18.
, т.к. HS есть объем треугольной призмы, равной половине объема V, т.е. 18.
Задача №6
Задача №7
|
из
5.00
|
Обсуждение в статье: Уравнение точки имеет следующий вид |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

