Программное вычисление

 

По блок-схеме была создана программа для вычисления интеграла методами Симпсона и трапеций:

 

// Вводим переменные:

var

Form2: TForm2;

a,b,E,h,S,S1,x: real; n, i: integer;

implementation

{ TForm2 }

uses unit1,unit3,unit4,unit5;

// Описываем функцию:

function f (x: real): real;

begin

f: =1/Sqrt (1+3*x+2*x*x);

end;

// В соответствие с блок-схемой напишем программу на языке высокого уровня:

procedure TForm2. MenuItem4Click (Sender: TObject);

begin

// найдем площадь интеграла по методу трапеций

S: =0; // изначально обнуляем значение площади интеграла

n: =1; // начальное значение количества разбиений

Repeat // начало цикла

S1: =S; // предыдущее значение площади изначально равно значению площади с количеством разбиений равным 1

n: =2*n; // увеличиваем количество разбиений в два раза

h: = (b-a) /n; // формула вычисления шага

S: =f (a) +f (b); // значение функции в нижнем пределе + значение функции в верхнем пределе определенного интеграла

x: =a; // значению x присвоим значение нижнего предела

for i: =1 to n-1 do // для i-того элемента, изменяющегося от 1 до n-1

begin

x: =x+h; // х увеличиваем на шаг

S: =S+2*f (x) // сумма площадей трапеций

end;

S: =S*h/2; // вычислим площадь по формуле

Until abs (S-S1) <=E; // если разность значения площади и предыдущего значения площади меньше или равна заданной точности Е, то

Form4. Edit1. Text: =FloatToStr (S); // выводим значение на экран

Form4. Caption: ='Вычисление методом трапеций';

Form4. Button2. visible: =True;

Form4. Chart1. Visible: =True;

Form4. ShowModal;

end;

procedure TForm2. MenuItem8Click (Sender: TObject);

begin

// найдем площадь интеграла по методу Симпсона (парабол)

S: =0; // начальное значение количества разбиений

n: =1; // изначально обнуляем значение площади интеграла

Repeat // начало цикла

S1: =S; // предыдущее значение площади изначально равно значению площади с количеством разбиений равным 1

n: =2*n; // увеличиваем количество разбиений в два раза

h: = (b-a) /n; // формула вычисления шага

S: =f (a) +f (b); // значение функции в нижнем пределе + значение функции в верхнем пределе определенного интеграла

x: =a; // значению x присвоим значение нижнего предела

for i: =0 to n do // для i-того элемента, изменяющегося от 1 до n-1

begin

x: =a+i*h; // х увеличиваем

if x=a then s: =s+f (x) else

if x=b then s: =s+f (x) else

if i mod 2 = 0 then s: =s+2*f (x) else s: =s+4*f (x); // если число четное, то вычисляется по формуле s: =s+2*f (x), а если нечетное, то по s: =s+4*f (x)

end;

S: =S*h/3; // вычислим площадь по формуле

Until abs (S-S1) <=E; // если разность значения площади и предыдущего значения площади меньше или равна заданной точности Е, то

Form4. Edit1. Text: =FloatToStr (S); // выводим значение на экран

Form4. Caption: ='Вычисление методом парабол';

Form4. Button2. visible: =False;

Form4. Chart1. Visible: =False;

Form4. ShowModal;

end;

Визуализация методов

 

Для открытия программы необходимо запустить project1. exe. После запуска откроется окно программы (рис.4). Предварительно создаем текстовый файл integral. txt в том же каталоге, где расположена программа (рис.9) в этом файле должны сохраниться результаты сравнения.

Запускаем программу. С помощью компонента MainMenu выберем вкладки "Ввод", "Решение", "Исследование" и "Заставка".

Выбираем вкладку "Ввод - Параметры" открывается Form 2 и вводим параметры (рис.10):

 

Рисунок 9 – Меню

 

Рисунок 10 - Параметры

 

Нажимаем на кнопку "OK" и возвращаемся к основной форме. Выбираем методы решения:

 

Рисунок 12 - Вычисление методов трапеций

 

Аналогично выглядит форма, когда вычисляем площадь по методу Симпсона (парабол). Далее выбираем вкладку "Исследование на погрешность" открывается Form 5, нажимаем на кнопку "График", затем на кнопку "Сохранить"

 

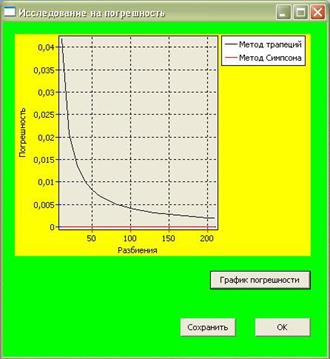
Рисунок 14 - Исследование на погрешность

 

Из графика видно, что метод Симпсона (парабол) намного точнее, почти совпадает с точным значением, вычисленным в пакете Maxima.

Затем на кнопку "Сохранить". Откроем каталог, где расположена программа и откроем текстовый файл integral. Txt

 

Рисунок 15 - Сохранение результатов сравнения

 

Нажмем на кнопку "OK" и вернемся в основной форме, чтобы завершить исследование вычислительных методов для нахождения интеграла.

 

Заключение

 

В процессе разработки курсовой работы были проработаны следующие методы вычисления определенных интегралов - метод трапеций и метод Симпсона (парабол). Был визуализирован ход вычисления интеграла в виде графика. На графике была представлена зависимость разбиений от заданной точности.

В процессе выполнения курсовой работы были закреплены практические навыки по разработке пользовательских приложений при помощи объектно-ориентированного языка программирования Lazarus и современных компьютерных технологий обработки информации, а также навыки в составлении текстовой документации.

Список литературы

 

1. Намиот Д.Е. Основные особенности языка программирования Delphi 7. - М.: ‘Память ’, 1999.

2. Пильщиков В.Н. Программирование на языке Delphi 7. - М.: Диалог--Мифи, 1999.

3. Михеева Е.В. Информационные технологии в профессиональной деятельности: Учебное пособие для сред. проф. образования. - 2-е издание, стер. - М.: Издательский центр "Академия", 2005. - 384 с.

4. Румянцева Е.Л., Слюсарь В.В. Информационные технологии: учеб. пособие / Под. ред. проф. Л.Г. Гагариной. - М.: ИД "ФОРУМ": ИНФРА - М, 2007. - 256 с.: ил.

5. Ильин В.А., Поздняк Э.Г. - Основы математического анализа. Часть 1 - М.: Физматлит, 2008 - 648 с.