VII. Проверка прочности валов.

Прочность валов проверим по гипотезе наибольших касательных напряжений.

Быстроходный вал.

Изготовление шестерни предусмотрено вместе с валом. Для материала вал-шестерня предел выносливости при симметричном цикле 0,43 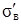 = 0,43 × 730 = 314 МПа.

Принимая [n] = 2,3, К_s = 2, K_s = 1 [s₄]_-1 = (s_-1/([n]К_s)) k_ри = (314/2,3 × ×2)1 = 68,3 МПа.

1. Вычерчиваем схему нагружения быстроходного вала и строим эпюры изгибающих и крутящих моментов.

2. Определяем реакции опор в вертикальной плоскости zO_y от сил F_a1 и F_r1 (рис. 2).

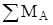= 0; F_a1 × 0,5 d_m1 – F_r1a₁ – Y_B × c₁ = 0;

Y_B =  = = – 4,9 Н;

= 0; Y_A× c₁ – F_j1 × 0,5 dm₁ – F_r (j₁ + c₁) = 0;

Y_А =  = = 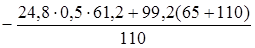150,9 Н­;

Проверка: –Y_B + Y_A – F_r1 = –49 + 150,9 – 99,2 = 0.

б) Определяем реакции опор в горизонтальной плоскости хО_z от силы F_t:

ΣМ_А = 0; Х_Вс₁ – F_ta₁ = 0;

X_B = Ft_a1/c₁ = 281 × 65/110 = 166 H;

Σ_МB = 0; –Х_Aс₁ – Ft(a₁ + c₁) = 0;

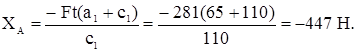
Проверка: X_B + F_t – X_A = 166 + 281 – 447 = 0.

в) Определяем размер изгибающих моментов в характерных сечениях в плоскости yO_z:

M_A = Y_ВС1 = –49 × 0,11 = –5,39 Н×м;

М_В = 0;

М_С = F_a1 × 0,5dm₁ = 24,8 × 0,5 × 0,0612 = 0,76 H×м.

Следовательно, M_Fa,Fr = –5,39 Н×м.

В плоскости хO_z:

М_В = М_С = 0;

М_А = –Х_ВС1 = –166 × 0,110 = –18,26 Н×м.

Следовательно, M_Ft = –18,26 Н×м.

Крутящий момент Т = Т₁ = 8,6 Н×м.

2. Вычисляем суммарный изгибающий момент и определяем нормальные напряжения изгиба в опасном сечении А при d = d₁^IV = 30 мм.

s_и = M_и/W_x = 32 M_и/(πd³) = 32 × 19/(314(30 × 10^–3)³) = 7,2 × 10⁶ Па.

3. Напряжение сжатия от силы F_a1 крайне малы и потому их можно не учитывать.

4. Определяем напряжение кручения в сечении А:

τ_к = Т/W_p = 16T₁/(πd³) = 16 × 8,6/(3,14(30 × 10^–3)³) = 1,62 × 10⁶ Па.

5. По гипотезе наибольших касательных напряжений находим эквивалентное напряжение и сравниваем его с допускаемым:

Тихоходный вал.

Для изготовления тихоходного вала принята сталь 40 (термообработка – нормализация), для которой по табл. П3 при d < 100 мм s_в = 550 МПа и, следовательно, предел выносливости s_–1 » 0,43_sв = 0,43 × 550 = 236 МПа.

Принимая [n] = 2,3, К_s = 2, k_ри = 1, вычисляем допускаемое напряжение прибора при симметричном цикле:

[s_и]_–1 = (s_–1/([n]K_s)) k_ри = (236/(2,3 × 2))1 = 51,3 МПа.

1. Вычеркиваем схему нагружения тихоходного вала и строим эпюры изгибающих и крутящих моментов.

а) Определяем реакции опор в вертикальной плоскости уОz от сил F_a2 и F_r2:

ZM_A = 0; F_a2 × 0,5d_m2 – F_r2a₂ + Y_B(a₂ + c₂) = 0;

Проверка: Y_A – F_r2 – Y_B = 103,3 – 24,8 – 76,5 = 0.

б) Определяем реакции опор в горизонтальной плоскости хО_z от силы F_t:

ΣM_B

X_B = F_ta₂/(a₂ + c₂) = 281 × 42/42 + 103 = 81,4 H;

ΣM_B = 0; –X_A(a₂ + c₂) + F_tc₂ = 0;

X_A = F_tc2/(a₂ + c₂) = 281 × 103/42 + 103 = 199,6 H.

Проверка: Х_А + Х_В – F_t = 199,6 + 81,4 – 281 = 0.

в) Определяем размер изгибающих моментов в характерных сечениях А и В:

в плоскости yO_z:

М_А = М_В = 0;

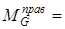Y_B c₂ = – 76,5 × 0,103 = –7,9 Н×м.

Следовательно, М_max = M_{Fa, Fr} = 7,9 H×м.

в плоскости хO_z:

М_А = М_В = 0;

М_с = Х_Аа₂ = 199,6 × 0,042 = 8,4 H×м.

Следовательно, М_Ft = 8,4 H×м.

Крутящий момент Т = Т₂ = 34,4 H×м.

2. Вычисляем суммарный изгибающий момент и определяем термальные напряжения изгиба в опасном сечении С:

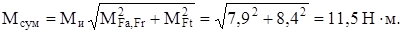
Так как вал в опасном сечении С ослаблен  = 36 мм) шпоночной канавкой, то при расчете следует уменьшить его диаметр на 8…10%. Принимая d = 32 мм, получаем

s_и = M_и/W_x = 32M_и/(πd³) = 32 × 11,5/(3,14(32 × 10^–3)³) = 3,57 × 10⁶ Па.

3. Напряжение сжатия ввиду их малости можно не учитывать.

4. Определяем касательные напряжения кручения в сечении С:

τ_к = Т/W_р = 16Т₂/(πd³) = 16 × 34,4/(3,14 × (32 × 10^–3)³) = 5,35 × 10⁶ Па.

5. Вычисляем эквивалентное напряжение и сравниваем его с допускаемым: