Четная и нечетная составляющие.

ГОУ ВПО

Уральский государственный горный университет

Институт геологии и геофизики Кафедра геоинформатики

620144 , г. Екатеринбург, ул. Куйбышева, 30

Тел. (343) – 2576661. E-mail: [email protected]

 

РЕФЕРАТ

Преобразование Хартли

Краткое содержание работы Р. Брейсуэлла

«Преобразование Хартли. Теория и приложения», М: Мир, 1990.

Курс: Теория цифровой обработки данных

Выполнила: Балаева Л.А.

E-mail: [email protected]

Руководитель : проф . Давыдов А.В.

E-mail: [email protected]

Содержание .

1. Введение.

2. Преобразование Хартли.

2.1. Четная и нечетная составляющие.

2.2. Формулы связи.

2.3. Энергетический и фазовый спектры.

3. Теоремы.

3.1. Соответствие операций.

3.2. Свертка.

4. Дискретное преобразование Хартли.

4.1. Физический смысл величин τ и ν.

4.2. Чётная и нечётная составляющие.

4.3. Степени свободы.

4.4. Другие вещественные ядра.

4.5. Теоремы, связанные с ДПХ.

4.6. Выводы по ДПХ.

5. Заключение.

Без сохранения форматирования исходного документа

Екатеринбург

2005

Введение.

Преобразование Хартли, как и преобразова­ние Фурье, может применяться для спектрального анализа и различных видов обработки сигналов. Данный вид преобразования назван в честь Р. Хартли, опубликовавшего в 1942 г. статью о паре интегральных преобразований - прямом и обратном, использующих введенную им функцию 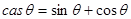. До начала 1980-х годов эти результаты оставались в забвении, пока к ним не привлек внимание исследователей Р. Брейсуэлл, разработавший основы тео­рии как непрерывного, так и дискретного преобразования Хартли, а также один из вариантов его быстрого преобразования.

Непрерывный прогресс в области обработки информации связан с задачами всевозрастающей сложности. Обращение к преобразованию Хартли обусловлено ситуацией, сложившейся в ряде методов обработки информации, в частности использующих вещественные последовательности данных (одномер­ных и двумерных). Обработку таких данных желательно осуществ­лять в области вещественных чисел с помощью взаимно симмет­ричных прямого и обратного преобразований. В отличие от преоб­разования Фурье, отображающего вещественные функции в ком­плексную область и несимметричного по i (происходит изменение знака при переходе от прямого к обратному преобразованию), пре­образование Хартли осуществляет прямое и обратное преобразо­вания только в вещественной области и обладает указанной сим­метрией.

В своём реферате я постараюсь изложить на основе теории и практических примеров некоторые основные аспекты преобразо­вания Хартли.

Эта тема является актуальной, так как в настоящее время преобразование Хартли находит широкое применение при разработке двумерных и трехмерных быстрых пре­образований, быстрых алгоритмов интерполяции и т.д.

Хартли ввел пару формул.

.

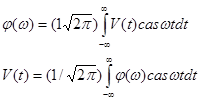В этих соотношениях для функции cas мы будем следовать определению автора, в соответствии с которым эта функция представляет собой сумму косинуса и синуса одного и того же аргумента cas t = cos t+ sin t.

 

2. Преобразование Хартли.

В определение Хартли для преобразования y (w) в явном виде был включен коэффициент 1/ 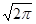 для получения симметричного вы­ражения. Если опустить этот коэффициент, то оба интеграла одновре­менно не могут быть корректными. Однако следует признать не­целесообразным сохранение пары таких специфических коэффициен­тов, особенно при выполнении численных расчетов. Многие авторы отреагировали на подобную ситуацию применительно к преобразо­ванию Фурье рассмотрением функции 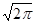S(w) вместо S(w).В результате коэффициент 1/  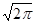исчезает в определении прямого преобразования Фурье, однако в формуле обратного преобразования Фурье появляется коэффициент 1/2p. Таким образом, эти авторы намеренно жертвуют симметрией формул. Справедливо замечание, что это дополнительная нагрузка для памяти, так как приходится запоминать, какая из формул содержит величину 2p .Один способ запоминания состоит в том, что коэффициент 1/2p стоит перед интегралом, в котором фигурирует дифференциал d w , что означает наличие величины вида w/2p , т. е. циклической частоты f. Отсюда естественно возникает вопрос: почему непосредственно не иметь дело с частотой? Именно к этому выводу в течение многих лет склонялось мнение разных исследователей. Приверженцев использования коэф­фициента 1/  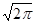в настоящее время практически уже нет, тогда как имеется достаточное количество сторонников правомерности записи d w /2p; но общепринятой практикой является применение множителя 2 p под знаком экспоненты в интегралах для прямого и обратного преобразований. Данная процедура реализуется автоматически при использовании частоты  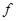вместо угловой частоты w. При этом имеем

 

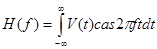
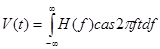
Четная и нечетная составляющие.

Взаимосвязь преобразований Фурье и Хартли базируется на анализе свойства симметрии. Для пояснения этого представим 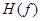 в виде четной и нечетной компонент  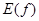и 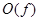 соответственно. Четная компонента определяется как полусумма функции  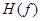и ее зер­кального изображения, т.е. функции 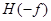. Нечетная компонента определяется как полуразность этих функций и обладает свойством антисимметрии, а именно 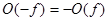. Любая функция может быть представлена однозначно в виде суммы четной и нечетной компонент, и, обратно, при заданных четной и нечетной компонентах однозначно может быть восстановлена исходная функция. Одним из интересных свойств четной и нечетной компонент является равенство суммы их энергий энергии самого процесса.

Для установления связи преобразования 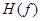с преобразованием Фурье 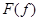функции 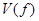примем следующее определение.

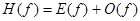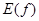Пусть где  и 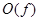 - соответственно четная и нечетная составляющие функции 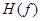. Тогда

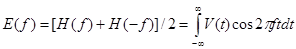
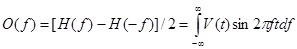
Эти два интеграла известны под названиями соответственно косинус- и синус-преобразование Фурье.

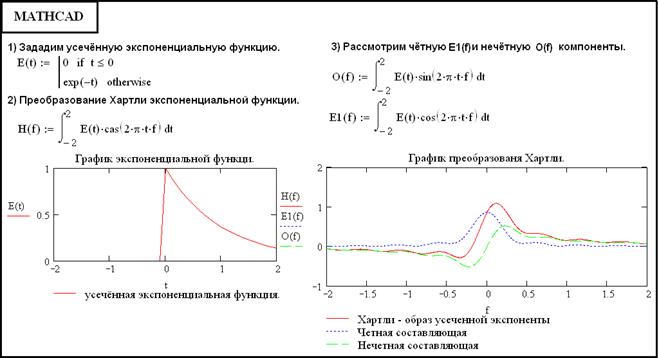
Для иллюстрации чётной и нечётной составляющей рассмотрим ряд примеров:

Пример №1. Рассмотрим функцию вида 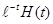, которая в момент времени t = 0 имеет еди­ничный скачок, а затем монотонно убывает по экспоненциальному закону. В данном выражении фигурирует единичная ступенчатая функция Хевисайда H ( t ), которая определяется следующим образом:

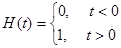
Заметим, что значение функции 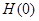, т. е.  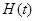при t = 0, не определено. Причина этого заключается в следующем. Рассмотрим две функци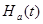и  и 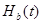, которые совпадают с 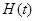при 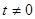, но в отличие от  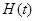определены при t = 0. Пусть Н_а (0) = а и Н_ь (0) = b . Тогда разность 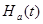- 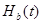представляет собой нулевую функцию. Поскольку рассматриваются интегралы, на их величину не влияет выбор какого-либо определенного конечного значения Н(0).

           Оцениваемый интеграл равен:

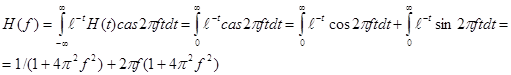
На данном примере №1 можно видеть симметрию чётной компоненты 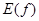 и её относительно быстрое убывание, и симметрию относительно начала координат нечётной составляющей .

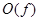Можно заметить, что H ( f ) не является ни четной, ни нечетной функцией. Минимум функции H ( f ) имеет место при 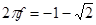,макси­мум при 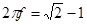, и она обращается в нуль 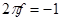при . При 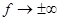 функция убывает как .

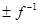Пример №2. Рассмотрим сигнал 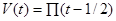,  где 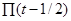- смещенная единичная прямоугольная функция, имею­щая свое начало при t = 0. Стандартная единичная прямоугольная функция, которая часто необходима для стробирования сегментов колебаний, определяется как

 

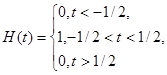
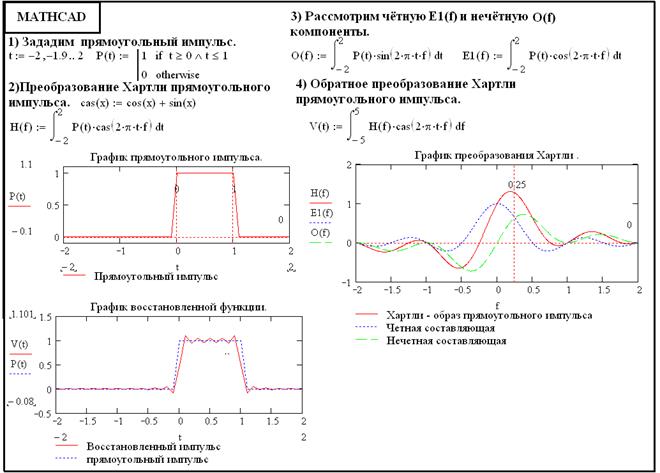
Для данного примера имеем преобразование Хартли

,

 

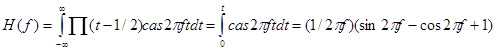Формулы связи.

При заданной функции 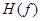 для получения преобразования Фурье 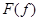можно сформировать сумму :

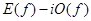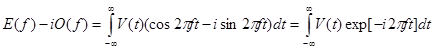
Таким образом, из 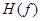легко получить преобразование Фурье ко­лебания V ( t ) путем формирования зеркального изображения вида 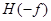и операций суммирования функций. Вещественная часть F ( f ) равна E ( f ), а мнимая часть противоположна по знаку функции :

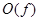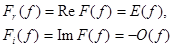
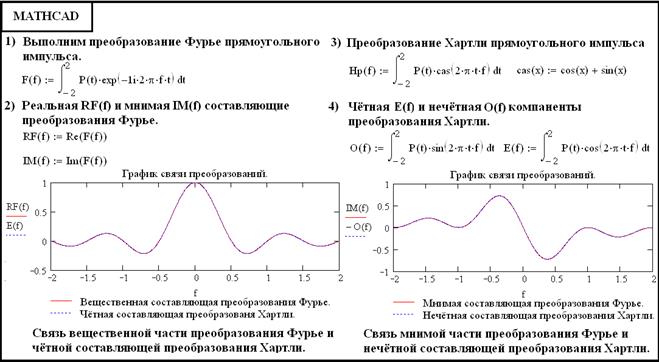
Наглядно связь преобразования Хартли с преобразованием Фурье можно представить на примере (в качестве примера возьмём стробирующую функцию)

 

 

И обратно, из заданного преобразования Фурье F ( f ) можнополучить 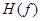, заметив, что

,

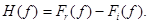т.е., исходя из F ( f ), функция 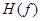 определяется как сумма ве­щественной части преобразования Фурье и ее мнимой части, взятой с обратным знаком.

Помня о том, что мнимая часть комплексной величины сама является вещественной, убеждаемся в том, что 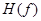представляет собой вещественную функцию, как и должно быть при условии, что исходное колебание  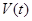вещественно. Если бы 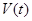не было ве­щественной функцией (в этом случае 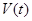не могло бы представлять собой напряжение электрического колебания), то 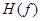, а тем более 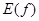и 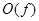также не были бы вещественными. В результате можно резюмировать:

Преобразование Фурье равно разности четной составляющей пре­ образования Хартли и нечетной составляющей, умноженной на i ; напротив, преобразование Хартли определяется как разность ве­щественной и мнимой составляющих преобразования Фурье.