 |
Главная |
Теоремы связанные с ДПХ.
|
из
5.00
|
 Каждой теореме дискретного преобразования Фурье соответствует подобная теорема для дискретного преобразования Хартли. Для полноты представления материала ниже даются все теоремы, в том числе теоремы о свертке и корреляции. Свертка функций непрерывного аргумента, обозначаемая символом
Каждой теореме дискретного преобразования Фурье соответствует подобная теорема для дискретного преобразования Хартли. Для полноты представления материала ниже даются все теоремы, в том числе теоремы о свертке и корреляции. Свертка функций непрерывного аргумента, обозначаемая символом  , отличается от процедуры циклической свертки дискретных последовательностей, для обозначения которой используется символ
, отличается от процедуры циклической свертки дискретных последовательностей, для обозначения которой используется символ  .
.
Можно отметить, что среднее значение последовательности  определяется величиной H(0), а значение ее среднего квадрата равно
определяется величиной H(0), а значение ее среднего квадрата равно  .
.


Некоторые теоремы для двух различных преобразований характеризуются точным соответствием, как, например  и
и  , тогда как в других случаях имеют место различия.
, тогда как в других случаях имеют место различия.
Теорема о зеркальном изображении. Если из последовательности  сформировать ее зеркальное изображение
сформировать ее зеркальное изображение  , то в результате ведущий (нулевой) элемент сохранит неизменное положение, а остальные элементы изменят порядок следования на обратный. Таким образом, вместо элемента f(1) исходной последовательности имеем f(-1), который интерпретируется как f(-1 mod N) и равен f(N-1), т.е. является последним элементом новой последовательности. Следовательно, вместо последовательности {a b c d e f g h}имеем {a h g f e d c b}, что в области преобразования соответствует замене вида {ABCDEFGH}
, то в результате ведущий (нулевой) элемент сохранит неизменное положение, а остальные элементы изменят порядок следования на обратный. Таким образом, вместо элемента f(1) исходной последовательности имеем f(-1), который интерпретируется как f(-1 mod N) и равен f(N-1), т.е. является последним элементом новой последовательности. Следовательно, вместо последовательности {a b c d e f g h}имеем {a h g f e d c b}, что в области преобразования соответствует замене вида {ABCDEFGH}  {AHGFEDСВ}.
{AHGFEDСВ}.
Теорема сложения. Свойство суперпозиции, иллюстрируемое теоремой сложения, просто отражает линейность оператора ДПХ.
Теорема о сдвиге. Сначала рассмотрим пример, в котором реализуется единичный сдвиг последовательности {a0 a1 a2 ... aN-1}, имеющей ДПХ вида {α0 α1 α2 ... αN-1}. В соответствии с теоремой о сдвиге для Т= 1 имеем последовательность {aN-1 а0 а1 аг … aN-2},для которой ДПХ равно
{ α 0 C1α1 C2a2 ... C N-1 αN-1} - { 0 S1α N-1S2αN-2... SN-1α1},
где Cν = cos (2πν/N), Sν = sin(2πν/N).
Для выполнения данной операция сдвига мы перемещаем каждый элемент исходной последовательности на одну позицию вправо. Последний элемент в соответствии с принятым свойством цикличности перемещается на первую позицию.
ДПХ состоит из двух последовательностей, одна из которых содержит косинусные, другая - синусные коэффициенты. ДПФ также представляет собой совокупность двух последовательностей с синусными икосинусными коэффициентами, однако для ДПХ в отличие от ДПФ для синусной компоненты характерно зеркальное отображение - это свойство именуется обратной индексацией. Для доказательства теоремы о сдвиге подставим f(t+T)вформулу, определяющую прямое ДПХ, и получим
 f(τ+T)cas(2πντ/N) =
f(τ+T)cas(2πντ/N) =  f(
f(  )cas[2πν(
)cas[2πν(  -T)/N] =
-T)/N] =
 f(
f(  )[cas (2πν
)[cas (2πν  /N) cos (2πνT/N) + cas'(2πν
/N) cos (2πνT/N) + cas'(2πν  /N) sin(2 πνT/N)] =
/N) sin(2 πνT/N)] =
cos (2πνT/N)  f(
f(  )cas(2πν
)cas(2πν  /N) + sin(2πνT/N)
/N) + sin(2πνT/N)  f(
f(  )cas'(2πνT/N) =
)cas'(2πνT/N) =
cos (2πνT/N) H(ν) - sin(2πνT/N)  f(
f(  )cas(-2πν
)cas(-2πν  /N) =
/N) =
cos(2πνT/N) H(ν) -sin(2πνT/N)H(-ν).
 Теорема о свертке. В общем случае преобразование свертки
Теорема о свертке. В общем случае преобразование свертки  (τ)
(τ)  f2(τ) содержит четыре компоненты. Основными величинами, которые должны быть вычислены, являются прямые произведения Ра(ν)= H1(ν)H2(ν) и смешанные произведения Рb(ν)=H1(ν)H2(-ν). С использованием этих обозначений имеем H(ν)=
f2(τ) содержит четыре компоненты. Основными величинами, которые должны быть вычислены, являются прямые произведения Ра(ν)= H1(ν)H2(ν) и смешанные произведения Рb(ν)=H1(ν)H2(-ν). С использованием этих обозначений имеем H(ν)=  N[Pa(ν)-Ра(-ν)+Рb(ν)+Рb(-ν)].
N[Pa(ν)-Ра(-ν)+Рb(ν)+Рb(-ν)].
Таким образом, данная процедура включает два, а не четыре действия умножения. Теперь если Н2(ν) - четная функция (т. е. Н2(ν)= H2(-ν)), то
H(ν) =  NHl(ν)H2(ν).
NHl(ν)H2(ν).
Рассмотрим пример, когда H2(ν) –чётная функция.

Точно так же простую формулу получим в случае, когда Н2(ν) является нечетной функцией; при этом имеем H(ν)=NHl(-ν)H2(ν).
Вследствие коммутативности Н(ν)=NHl(ν)H2(ν), если либо H1(ν), либо Н2(ν) являются четными функциями. Часто одна либо другая функция обладает свойствами симметрии или антисимметрии, что приводит к более простым соотношениям. Ввиду важности операции свертки мы вернемся к ней в следующей главе.
Теорема о произведении. В теореме о произведении четыре компоненты предполагают выполнение только двух операций свертки, так как две другие просто реализуются путем зеркального отображения двух сомножителей.
Теорема о растяжении. Сходство этой теоремы с соответствующей теоремой для случая непрерывной независимой переменной относится к изменению масштаба по оси абсцисс, когда V(t)преобразуется в V(t/T).Так как величина T может быть либо больше, либо меньше единицы, операция может представлять собой либо растяжение, либо сжатие. В случае дискретной переменной изменения масштаба также имеют практическое значение, например, когда последовательность регулярных измерений должна быть повторена с большей или меньшей скоростью. Функция V(t/T)определена для любого Т при заданной V(t), но это утверждение несправедливо для f(τ/Т) при заданной функции f(τ), где τ=0,1, … ,N-1. Следовательно, применительно к теореме подобия отсутствует строгая аналогия. Теорема о растяжении имеет отношение только к увеличению масштаба времени, что осуществляется добавлением нулей в исходную последовательность. Наиболее просто это можно проиллюстрировать на примере.
Пусть последовательность {abcd}имеет последовательность ДПХ {α β γ δ}. Тогда последовательности {а 0 b 0 с 0 d 0} соответствует последовательность ДПХ вида  {α β γ δ α β γ δ }.
{α β γ δ α β γ δ }.
В правомерности этого результата можно убедиться, анализируя выражение для прямого ДПХ:
 α+
α+  βcas τθ+
βcas τθ+  γcas 2τθ+
γcas 2τθ+  δcas 3τθ+
δcas 3τθ+  αcas 4τθ+
αcas 4τθ+  βcas 5τθ+
βcas 5τθ+  γcas 6τθ+
γcas 6τθ+  δcas7τθ.
δcas7τθ.
Убеждаемся в том, что при τ = 0 имеем f(0) = а. При нечетном τ сумма равна нулю, для четного τ эта сумма сводится к выражению: α+βcasτθ+γcas2τθ+δcas3τθ, для которого обратное преобразование Хартли имеет вид: {a b c d}.
Теорема о второй производной. Рассмотрим данную теорему на примере экспоненциальной функции.

Выводы по ДПХ.
Свойства ДПХ свидетельствуют в пользу использования этого преобразования в численном анализе. Тот факт, что значения преобразования Хартли являются вещественными, создает удобства при выполнении расчетов. Кроме того, полезно свойство симметрии обращения преобразования, так как не требуется запоминать, к какой области представления относится данная последовательность. Более того, ряд теорем для преобразования Фурье имеет различную форму для разных областей представления (временной или частотной); этот недостаток отсутствует у ДПХ. Множитель N зависит от области представления, и от него можно было бы избавиться, однако на практике почти всегда существуют нормирующие или калибровочные факторы, которые должны быть учтены по окончании численных расчетов. Опыт показывает, что последний этап заключается в учете в совокупной форме коэффициентов пропорциональности, поэтому отклонение от точного соответствия между прямым и обратным преобразованиями, заключающееся в появлении коэффициента N,не имеет значения в практике вычислений.
Заключение.
Таким образом, в данном реферате были рассмотрены некоторые основы преобразования Хартли. В результате чего можно сделать следующие выводы.
Во-первых, хотя между интегралами преобразования Хартли

отсутствуют существенные отличия от обычных интегральных формул преобразования Фурье, однако на практике эти различия значительны.
Во-вторых, функция 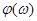 вещественна в отличие от функции преобразования Фурье.
вещественна в отличие от функции преобразования Фурье.
В-третьих, обратное преобразование для его реализации требует точно такой же процедуры интегрирования, как и прямое преобразование.
Наконец, 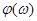 не является обычным преобразованием Фурье, и мы должны быть готовы к нетрадиционным характеру и свойствам этого преобразования. Значительная часть умозрительных построений относительно преобразования Фурье, а, именно спектра колебания, являющегося функцией времени, непосредственно неприменима к
не является обычным преобразованием Фурье, и мы должны быть готовы к нетрадиционным характеру и свойствам этого преобразования. Значительная часть умозрительных построений относительно преобразования Фурье, а, именно спектра колебания, являющегося функцией времени, непосредственно неприменима к 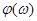 .
.
|
из
5.00
|
Обсуждение в статье: Теоремы связанные с ДПХ. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

