Статистические характеристики интервального ряда

 

1. Исходными данными для расчета статистических характеристик интервального ряда является интервальный ряд, полученный в предыдущей пункте.

2. Для удобства вычислений составим вспомогательную таблицу, содержащую промежуточные данные. Ее можно расположить на новом рабочем листе (см. табл.3.6 рис.2.6). Данные колонок x_SRi, f_i, s_i копируются в новый рабочий лист из предыдущего листа (табл.3.5 рис. 2.1). Для этого необходимо выполнить следующие действия: выделить копируемый блок ячеек из табл.3.5 рис.2.1, выполнить команду /Правка/копировать, перейти на новый лист, указать блок-получатель (левую верхнюю ячейку), выполнить команду /Правка/специальная вставка/значения.

3.

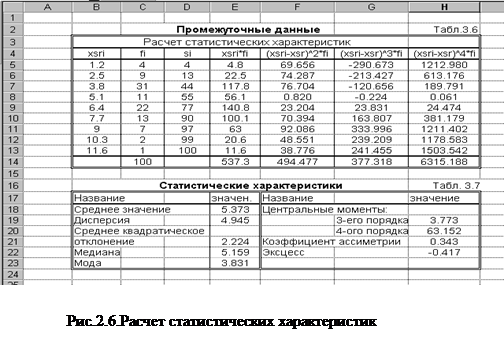Выполнить расчет в колонке x_Sri*f_i.Для этого в первую ячейку колонки E5 ввести формулу [=B5*C5], затем выполнить копирование ее в остальные ячейки колонки.

 

4. Используя функцию СУММ() или нажать кнопку Автосуммирование, определить итоговые суммы в колонках f_i и x_SRi×f_i (ячейки C14, E14).

5. Рассчитать среднее значение 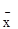. Для этого в ячейку E18 ввести формулу [=E14/C14].

6. В следующих колонках выполнить вычисления: (x_sri -`x )<sup>2</sup>×f<sub>i</sub>, (x<sub>sri</sub> -`x)³×f_i, (x_sri -`x)<sup>4</sup>×f<sub>i</sub>. Необходимо помнить, что `x - средняя арифметическая является скалярной величиной, поэтому ссылка на ячейку, содержащую значения `x должна быть абсолютной. Формулы в ячейках F5, G5, H5 будут такими: [=(B5-$F$18)^2*C5], [=(B5-$F$18)^3*C5], [=(B5-$F$18)^4*C5]. Выполнить копирование формул в остальные ячейки колонок таблицы.

7. Вычислить итоговые суммы в колонках "(x_sri -`x )<sup>2</sup>×f<sub>i</sub>", "(x<sub>sri</sub> -`x)³×f_i", "(x_sri -`x)⁴×f_i". Для этого используется встроенная функция СУММ() или нажать кнопку Автосуммирования.

8. Рассчитать значения дисперсии d², среднего квадратического отклонения d, центральных моментов М₃, М₄, коэффициента асимметрии A_S, показателя эксцесса Е. (2.7, 2.8, 2.9, 2.10). Результаты расчета оформляются в виде табл.3.7 рис.2.6. В соответствующие ячейки колонок "значения" записываются следующие формулы: в E19 – [=F14/C14], в E21 – [=КОРЕНЬ(Е19)], в H19 – [=G14/C14], в H20 – [= H14/C14], в H21 – [=H19/E21^3], в H22 – [=H20/E21^4-3].

9. Рассчитываются значения медианы М_е и моды М_о. (2.11, 2.12). Т.к. значение частоты fi в i-ой строке таблицы соответствует интервалу [x_i-1;x_i], то в качестве начала медианного интервала x_me и модального интервала x_mo берутся значения интервала из предшествующих строк таблицы. В расчетных формулах используются данные x_me, x_moиз табл. 3.5, расположенной на другом рабочем листе (например ЛИСТ1), то для правильной адресации в расчетных формулах используются консолидированные ссылки. Формулы в ячейках для x_me и x_mo будут соответственно выглядеть так: в ячейке E22 – [=Лист1!В33+Лист1!G22*(Лист1!G17/2-D7)/C8], в ячейке E23 – [=ЛИСТ1!В32+ЛИСТ1!G22*(C7-C6)/(2*C7-C6-C8)].

 

Проверка гипотезы о нормальном распределении

Интервального ряда

1. Исходными данными для проверки гипотезы являются интервальный ряд (табл.3.5, рис.2.1.) и статистические характеристики интервального ряда (табл.3.7, рис.2.6).

2. Для удобства вычислений составляется вспомогательная таблица (табл. 3.8), которую можно создать на новом рабочем листе (рис.2.7).

Значения колонок x_SRi и f_i копируются из табл.3.5 (команды: /Правка/копировать и /Правка/специальная вставка/значения).

3. При малых значениях частот (менее 3) рекомендуется объединять интервалы. При объединении интервалов частоты складываются и пересчитывается среднее значение переменной в объединенном интервале. В рассматриваемом примере это касается последнего и предпоследнего интервалов. Полученные при объединении средние значения интервалов и частоты представлены в колонках x^'_SRi и f_i^'. При объединении в ячейках D12 и E12 записываются следующие формулы [=(B12+B13)/2] и [=C12+C13].

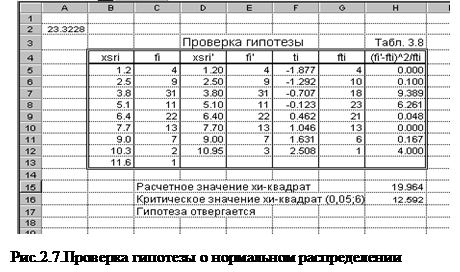
4. Выполнить расчеты в колонках t_i, f_i^t, (f_i^'- f_i^t)²/f_i^t (2.13, 2.14, 2.15]. При расчете f_i^t по формуле (2.13) предварительно в любой свободной ячейке (например в ячейке А2) рассчитаем промежуточную скалярную величину . Формула в ячейке А2 будет иметь вид:

=Лист1!G22*Лист1!G17/Лист2!E21/КОРЕНЬ(2*ПИ())

После этого в ячейки F5, G5, H5 вводим следующие формулы:

в ячейке F5 - =[(D5-Лист1!$E$18)/Лист1!$E$21],

в ячейке G5 - =ОКРУГЛ($A$2*EXP(-0.5*F5^2);0),

в ячейке H5 - =[(E5-G5)^2/G5].

Пояснение: на Лист1 расположены параметры интервального ряда; на Лист2 – статистические характеристики интервального ряда. Теоретическая частота, рассчитываемая по формуле (2.15), является дробной величиной. Она округляется до ближайшего целого с помощью функции ОКРУГЛ().

5. Значение суммы в колонке 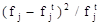 есть искомое значение критерия  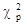Пирсона. Для вычисления суммы используется встроенная функция СУММ() или кнопка "Автосуммирования".

6. Для определения критического значения c²_кр можно воспользоваться встроенной функцией ХИ2ОБР(a,m) при уровне значимости a=0,05 и числе степеней свободы m=k-2. Для данных примера расчетное значение c²_p=19,964, критическое значение c²_kr=12,592. Т.к. c²_p>c²_kr, то гипотеза о нормальном распределении отвергается.

 

Построение графиков

 

1. Исходными данными для построения графиков является интервальный ряд (табл.3.5 рис.2.1).

2. Выполнить команду /Вставка/Диаграмма/ либо нажать кнопку Мастера диаграмм. Это действие раскрывает диалоговое окно Мастер диаграмм. Мастер диаграмм представляет собой серию диалоговых окон для управления режимом построения диаграмм и установки параметров диаграмм. Построение диаграмм осуществляется по шагам - 4 шага. На каждом шаге раскрывается соответствующее диалоговое окно Мастера диаграмм. Диалоговые окна имеют несколько вкладок, которые открываются кнопками, расположенными в верхней части диалоговых окон. В нижней части окон Мастера диаграмм изображены кнопки Отмена, <Назад, Далее>, Готово. Кнопка Отмена прекращает построение диаграмм и закрывает окно Мастера диаграмм. Кнопка Далее> осуществляет переход к следующему шагу построения диаграмм. Кнопка <Назад позволяет вернуться к предыдущему шагу при необходимости исправить установки на предыдущих шагах. Окна имеют одно или несколько строк ввода для установки значений параметров диаграмм.

3. Окно шаг 1 из 4 Мастера диаграмм предлагает выбрать тип диаграммы. Excel имеет возможность выбора 14 различных типов стандартных диаграмм. Каждый тип в свою очередь имеет насколько форматов. Окно имеет две вкладки - стандартные и нестандартные. Открываем вкладку стандартные и выбираем следующие типы диаграмм: для гистограммы - "гистограмма", для полигона частот и кумулятивной кривой - "график".

4. Окно Шаг 2 из 4 Мастера диаграмм предлагает выбрать данные для построения диаграммы, положение данных в таблице (по строкам или столбцам), данные для разметки оси Х. Для выбора данных раскрываем вкладку Диапазон данных, активизируем строку ввода диапазон, открываем лист, содержащий интервальный ряд. Далее выделяем соответствующий блок ячеек: построение гистограммы и полигона частот осуществляется по данным колонки f_i табл.3.5 рис.2.3, кумулятивная кривая строится по данным колонки s_i. Вкладка Ряды позволяет выбрать данные для разметки оси Х. Активизируем в ней строку ввода Подписи оси Х и в табл.3.5 выделяем данные для разметки оси Х: для гистограммы и кумулятивной кривой это будут данные столбца x_i, для полигона - данные столбца x_SRi.

5. Окно Шаг 3 из 4 Мастера диаграмм предлагает установить следующие параметры диаграмм: название диаграммы, названия оси Х и оси У, надписи на осях, установить координатную сетку или ее отменить, изменить размещение легенд. Открываем вкладку Заголовки и поочередно активизируя соответствующие строки ввода, вводим название диаграммы и название осей. Вкладка Оси позволяет установить или убрать разметку осей. Вкладка Подписи данных позволяет установить или убрать подписи значений данных на диаграмме. Вкладка Линии сетки позволяет изменить координатную сетку или убрать ее совсем. Вкладка Таблица данных позволяет поместить таблицу значений признака под диаграммой.

6. Окно Шаг 4 из 4 Мастера диаграмм предлагает поместить диаграмму на отдельном листе или на существующем. Выбираем на существующем. После этого нажать кнопку Готово.

7. При неудовлетворительном выборе параметров диаграмм и графиков можно выполнить редактирование соответствующих элементов (см.п.1.9).

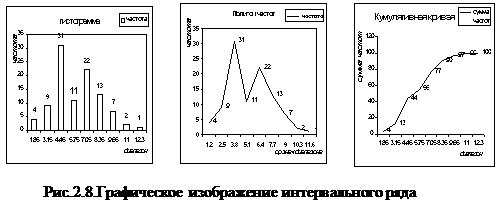8. Гистограмма, полигон частот и кумулятивная кривая изображены на рис.2.8.