 |
Главная |
Математическая статистика
|
из
5.00
|
1. Генеральная совокупность и выборка
В предыдущем разделе нас интересовала распределение признака в некоторой совокупности элементов. Совокупность, которая объединяет все элементы, имеющая этот признак, называется генеральный. Если признак человеческий (национальность, образование, коэффициент IQ т.п.), то генеральная совокупность — все население земли. Это очень большая совокупность, то есть число элементов в совокупности n велико. Число элементов называется объемом совокупности. Совокупности могут быть конечными и бесконечными. Генеральная совокупность – все люди хотя и очень большая, но, естественно, конечная. Генеральная совокупность – все звезды, наверное, бесконечно.
Если исследователь проводит измерение некоторой непрерывной случайной величины X, то каждый результат измерения можно считать элементом некоторой гипотетической неограниченной генеральной совокупности. В этой генеральной совокупности бесчисленная количество результатов распределены по вероятности под влиянием погрешностей в приборах, невнимательности экспериментатора, случайных помех в самом явлении и др.
Если мы проведем n повторных измерений случайной величины Х, то есть получим n конкретных различных численных значений 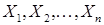 , то этот результат эксперимента можно считать выборкой объема n из гипотетической генеральной совокупности результатов единичных измерений.
, то этот результат эксперимента можно считать выборкой объема n из гипотетической генеральной совокупности результатов единичных измерений.
Естественно считать, что действительным значением измеряемой величины является среднее арифметическое от результатов 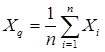 . Эта функция от n результатов измерений называется статистикой, и она сама является случайной величиной, имеющей некоторое распределение называемая выборочным распределением. Определение выборочного распределения той или иной статистики — важнейшая задача статистического анализа. Ясно, что это распределение зависит от объема выборки n и от распределения случайной величины Х гипотетической генеральной совокупности. Выборочное распределение статистики
. Эта функция от n результатов измерений называется статистикой, и она сама является случайной величиной, имеющей некоторое распределение называемая выборочным распределением. Определение выборочного распределения той или иной статистики — важнейшая задача статистического анализа. Ясно, что это распределение зависит от объема выборки n и от распределения случайной величины Х гипотетической генеральной совокупности. Выборочное распределение статистики 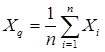 представляет собой распределение Хq в бесконечной совокупности всех возможных выборок объема n из исходной генеральной совокупности.
представляет собой распределение Хq в бесконечной совокупности всех возможных выборок объема n из исходной генеральной совокупности.
Можно проводить измерения и дискретной случайной величины.
Пусть измерение случайной величины Х представляет собой бросание правильной однородной треугольной пирамиды, на гранях которой написаны числа 1, 2, 3, 4. Дискретная, случайная величина Х имеет простое равномерное распределение:

Эксперимент можно производить неограниченное число раз. Гипотетической теоретической генеральной совокупностью является бесконечная совокупность, в которой имеются одинаковые доли (по 0.25) четырех разных элементов, обозначенных цифрами 1, 2, 3, 4. Серия из n повторных бросаний пирамиды или одновременное бросание n одинаковых пирамид можно рассматривать как выборку объема n из этой генеральной совокупности. В результате эксперимента имеем n чисел 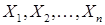 . Можно ввести некоторые функции этих величин
. Можно ввести некоторые функции этих величин 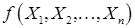 , которые называются статистиками, они могут быть связаны с определенными параметрами генерального распределения.
, которые называются статистиками, они могут быть связаны с определенными параметрами генерального распределения.
Важнейшими числовыми характеристиками распределений являются вероятности Рi, математическое ожидание М, дисперсия D. Статистиками для вероятностей Рi являются относительные частоты 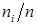 , где ni — частота результата i (i=1,2,3,4) в выборке. Математическому ожиданию М соответствует статистика
, где ni — частота результата i (i=1,2,3,4) в выборке. Математическому ожиданию М соответствует статистика
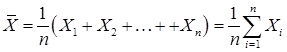 ,
,
которая называется выборочным средним. Выборочная дисперсия
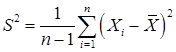 ,
,
соответствует генеральной дисперсии D.
Относительная частота любого события 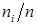 (i=1,2,3,4) в сериях из n повторных испытаний (или в выборках объема n из генеральной совокупности) будет иметь биномиальное распределение.
(i=1,2,3,4) в сериях из n повторных испытаний (или в выборках объема n из генеральной совокупности) будет иметь биномиальное распределение.

У этого распределения математическое ожидание равно 0.25 (не зависит от n), а среднее квадратическое отклонение равно 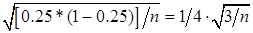 (быстро убывает с ростом n). Распределение является выборочным распределением статистики, относительная частота любого из четырех возможных результатов единичного бросания пирамиды в n повторных испытаниях. Если бы мы выбрали из бесконечной, генеральной совокупности, в которой четыре разных элемента (i=1,2,3,4) имеют равные доли по 0.25, все возможные выборки объемом n (их число также бесконечно), то получили бы так называемую математическую выборку объема n. В этой выборке каждый из элементов (i=1,2,3,4) распределен по биномиальному закону.
(быстро убывает с ростом n). Распределение является выборочным распределением статистики, относительная частота любого из четырех возможных результатов единичного бросания пирамиды в n повторных испытаниях. Если бы мы выбрали из бесконечной, генеральной совокупности, в которой четыре разных элемента (i=1,2,3,4) имеют равные доли по 0.25, все возможные выборки объемом n (их число также бесконечно), то получили бы так называемую математическую выборку объема n. В этой выборке каждый из элементов (i=1,2,3,4) распределен по биномиальному закону.
Допустим, мы выполнили 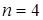 бросания этой пирамиды, и число двойка выпало 3 раза (
бросания этой пирамиды, и число двойка выпало 3 раза ( 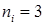 ). Мы можем найти вероятность этого результата, используя выборочное распределение. Она равна
). Мы можем найти вероятность этого результата, используя выборочное распределение. Она равна
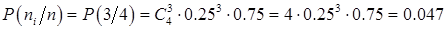 .
.
Наш результат оказался весьма маловероятным; в серии из двадцати четырех кратных бросаний он встречается примерно один раз. В биологии такой результат обычно считается практически невозможным. В этом случае у нас появится сомнение: является пирамида правильной и однородной, справедливо ли при одном бросании равенство 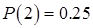 , верно ли распределение и, следовательно, выборочное распределение.
, верно ли распределение и, следовательно, выборочное распределение.
Чтобы разрешить сомнение, надо выполнить еще один раз четырехкратное бросание. Если снова появится результат 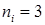 , то вероятность двух результатов с
, то вероятность двух результатов с 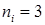 очень мала
очень мала 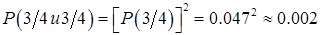 . Ясно, что мы получили практически совершенно невозможный результат. Поэтому исходное распределение неверное. Очевидно, что, если второй результат окажется еще маловероятней
. Ясно, что мы получили практически совершенно невозможный результат. Поэтому исходное распределение неверное. Очевидно, что, если второй результат окажется еще маловероятней 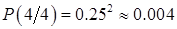 , то имеется еще большее оснований разобраться с этой "правильной" пирамидой. Если же результат повторного эксперимента будет
, то имеется еще большее оснований разобраться с этой "правильной" пирамидой. Если же результат повторного эксперимента будет 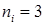 и
и 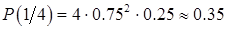 , тогда можно считать, что пирамида правильная, а первый результат (
, тогда можно считать, что пирамида правильная, а первый результат ( 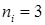 ), тоже верный, но просто маловероятный.
), тоже верный, но просто маловероятный.
Нам можно было и не заниматься проверкой правильности и однородности пирамиды, а считать априори пирамиду правильной и однородной, и, следовательно, правильным выборочное распределение. Далее следует выяснить, что дает знание выборочного распределения для исследования генеральной совокупности. Но поскольку установление выборочного распределения является основной задачей статистического исследования, подробное описание экспериментов с пирамидой можно считать оправданным.
Будем считать, что выборочное распределение верное. Тогда экспериментальные значения относительной частоты 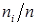 в различных сериях по n бросаний пирамиды будут группироваться около значения 0.25, являющегося центром выборочного распределения и точным значением оцениваемой вероятности. В этом случае говорят, что относительная частота
в различных сериях по n бросаний пирамиды будут группироваться около значения 0.25, являющегося центром выборочного распределения и точным значением оцениваемой вероятности. В этом случае говорят, что относительная частота 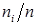 является несмещенной оценкой
является несмещенной оценкой 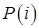 . Поскольку, выборочная дисперсия
. Поскольку, выборочная дисперсия 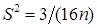 стремиться к нулю с ростом n, то экспериментальные значения относительной частоты будут все теснее группироваться около математического ожидания выборочного распределения с ростом объема выборки. Поэтому
стремиться к нулю с ростом n, то экспериментальные значения относительной частоты будут все теснее группироваться около математического ожидания выборочного распределения с ростом объема выборки. Поэтому 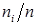 является состоятельной оценкой вероятности
является состоятельной оценкой вероятности 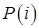 .
.
Если бы пирамида оказалась направильной и неоднородной, то выборочные распределения для различных (i=1,2,3,4) имели бы отличные математические ожидания (разные 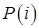 ) и дисперсии.
) и дисперсии.
Отметим, что полученные здесь биномиальные выборочные распределения при больших n ( 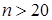 ) хорошо апроксимируются нормальным распределением с параметрами
) хорошо апроксимируются нормальным распределением с параметрами 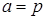 и
и 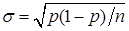 , что значительно упрощает расчеты.
, что значительно упрощает расчеты.
Продолжим случайный эксперимент — бросание правильной, однородной, треугольной пирамиды. Случайная величина Х, связанная с этим опытом, имеет распределение. Математическое ожидание здесь равно
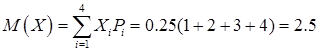 .
.
Проведем n бросаний, что эквивалентно случайной выборке объема n из гипотетической, бесконечной, генеральной совокупности, содержащей равные доли (0.25) четырех разных элементов. Получим n выборочных значений случайной величины Х (  ). Выберем статистику, которая представляет собой выборочное среднее. Величина
). Выберем статистику, которая представляет собой выборочное среднее. Величина 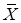 сама является случайной величиной, имеющей некоторое распределение, зависящее от объема выборки и распределения исходной, случайной величины Х. Величина
сама является случайной величиной, имеющей некоторое распределение, зависящее от объема выборки и распределения исходной, случайной величины Х. Величина 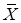 является усредненной суммой n одинаковых, случайных величин (то есть с одинаковым распределением). Ясно, что
является усредненной суммой n одинаковых, случайных величин (то есть с одинаковым распределением). Ясно, что
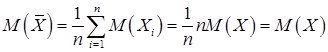 .
.
Поэтому статистика 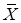 является несмещенной оценкой математического ожидания. Она является также состоятельной оценкой, поскольку
является несмещенной оценкой математического ожидания. Она является также состоятельной оценкой, поскольку
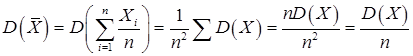 .
.
Таким образом, теоретическое выборочное распределение имеет тоже математическое ожидание, что и у исходного распределения, дисперсия уменьшена в n раз.
Напомним, что 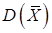 равна
равна
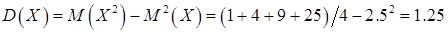 .
.
Математическая, абстрактная бесконечная выборка, связанная с выборкой объема n из генеральной совокупности и с введенной статистикой будет содержать в нашем случае 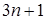 элементов. Например, если
элементов. Например, если 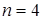 , то в математической выборке будут элементы со значениями статистики
, то в математической выборке будут элементы со значениями статистики 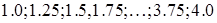 . Всего элементов будет 13. Доля крайних элементов в математической выборке будет минимальной, так как результаты
. Всего элементов будет 13. Доля крайних элементов в математической выборке будет минимальной, так как результаты 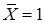 и
и 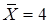 имеют вероятности, равные
имеют вероятности, равные 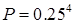 . Среди множества элементарных исходов четырех кратного бросания пирамиды имеются только по одному благоприятному
. Среди множества элементарных исходов четырех кратного бросания пирамиды имеются только по одному благоприятному 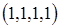 и
и 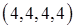 . При приближении статистик к средним значениям, вероятности будут возрастать. Например, значение
. При приближении статистик к средним значениям, вероятности будут возрастать. Например, значение 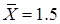 будет реализоваться при элементарных исходах
будет реализоваться при элементарных исходах 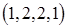 ,
, 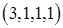 ,
, 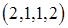 и т. д. Соответственно возрастет и доля элемента 1.5 в математической выборке.
и т. д. Соответственно возрастет и доля элемента 1.5 в математической выборке.
Среднее значение будет иметь максимальную вероятность. С ростом n экспериментальные результаты будут теснее группироваться около среднего значения. То обстоятельство, что среднее выборочного среднего 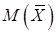 равно среднему исходной совокупности
равно среднему исходной совокупности 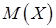 часто используется в статистике.
часто используется в статистике.
Если выполнить расчеты вероятностей в выборочном распределении с 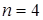 , то можно убедиться, что уже при таком небольшом значении n выборочное распределение будет выглядеть как нормальное. Оно будет симметричным, в котором значение
, то можно убедиться, что уже при таком небольшом значении n выборочное распределение будет выглядеть как нормальное. Оно будет симметричным, в котором значение 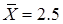 будет медианой, модой и математическим ожиданием. С ростом n оно хорошо апроксимируется соответствующим нормальным даже, если исходное распределение прямоугольное. Если же исходное распределение нормально, то распределение
будет медианой, модой и математическим ожиданием. С ростом n оно хорошо апроксимируется соответствующим нормальным даже, если исходное распределение прямоугольное. Если же исходное распределение нормально, то распределение 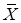 является распределением Стьюдента при любом n.
является распределением Стьюдента при любом n.
Для оценки генеральной дисперсии 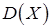 необходимо выбрать более сложную статистику, которая дает несмещенную и состоятельную оценку
необходимо выбрать более сложную статистику, которая дает несмещенную и состоятельную оценку 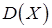 . В выборочном распределении для S2 математическое ожидание равно
. В выборочном распределении для S2 математическое ожидание равно 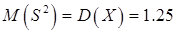 , а дисперсия
, а дисперсия 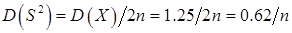 . При больших объемах выборок выборочное распределение можно считать нормальным. При малых n и нормальном исходном распределении выборочное распределение для S2 будет χ2‑распределение.
. При больших объемах выборок выборочное распределение можно считать нормальным. При малых n и нормальном исходном распределении выборочное распределение для S2 будет χ2‑распределение.
Выше мы попытались представить первые шаги исследователя, пытающегося провести простой статистический анализ повторных экспериментов с правильной однородной треугольной призмой (тетраэдром). В этом случае нам известно исходное распределение. Можно в принципе теоретически получить и выборочные распределения относительной частоты, выборочного среднего и выборочной дисперсии в зависимости от числа повторных опытов n. При больших n все эти выборочные распределения будут приближаться к соответствующим нормальным распределениям, так как они представляют собой законы распределения сумм независимых случайных величин (центральная предельная теорема). Таким образом, нам известны ожидаемые результаты.
Повторные эксперименты или выборки дадут оценки параметров выборочных распределений. Мы утверждали, что экспериментальные оценки будут правильными. Мы не выполняли эти эксперименты и даже не приводили результаты опытов, полученные другими исследователями. Можно подчеркнуть, что при определении законов распределений теоретические методы используются чаще, чем прямые эксперименты.
|
из
5.00
|
Обсуждение в статье: Математическая статистика |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

