Интервальный вариационный ряд

 

Как уже отмечалось выше, для непрерывной случайной величины всю область ее возможных значений нужно разделить на интервалы, которые называют классами. Обычно ширины всех классов выбирают одинаковыми. Ширину интервалов ΔX определяют формулой

 

,

 

где X_max и X_min — наибольшее и наименьшее значение признака в выборке, а k — количество классов. Оптимальное число классов зависит от объема выборки. При этом используют таблицу

 

Объем выборки — n	25 ¸ 40	40 ¸ 60	60 ¸ 100	100 ¸ 200	200 ¸ 1000
Число классов — k	5 ¸ 6	6 ¸ 8	7 ¸ 10	8 ¸ 12	10 ¸ 15

 

Количество вариант в классе есть частота попадания в данный класс. Все классы кроме последнего представляют собой полуоткрытые справа интервалы (например ), а последний закрытый . Можно составить таблицу интервальных вариационных рядов; ее общий вид таков:

 

 

Здесь a_i – границы классовых интервалов.

Если на оси абсцисс отложить классовые интервалы и над ними построить прямоугольники с высотами, равными соответствующим плотностям f_i относительной частоты, то площадь каждого прямоугольника будет равна относительной частоте 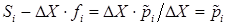. Полученная таким образом ступенчатая фигура называется гистограммой. Площадь под гистограммой равна единице, так как она равна сумме площадей всех прямоугольников . Понятно, что линия, которая идет по оси абсцисс, затем огибает гистограмму и затем снова идет по оси абсцисс является графиком эмпирической функции плотности вероятности.

Интервальный вариационный ряд можно построить и для дискретной случайной величины, если объем выборки достаточно большой. Нужно, чтобы в каждом классе было не менее трех вариант. В этом случае мы как бы совершаем переход от дискретной случайной величины к непрерывной.

Рассмотрим пример. Измерена частота пульса X_i (число сокращений сердца за минуту) у 1060 студентов (  — объем выборки), , . Выборка очень большая, поэтому выберем число классов . Тогда , то есть в интервале содержится четыре значения Х (здесь у нас дискретная случайная величина). Допустим, на основании имеющихся вариант мы построили таблицу интервальных вариационных рядов.

 

№ класса	Классовый интервал	Частота mi	Отн. частота pi	Плотность отн. частоты fi	Комулятивная отн. частота Fi
1	[43;47[	1	0.0008	0.0002	0 ¸ 0.0008
2	[47;51[	3	0.0028	0.0007	0.0008 ¸ 0.0036
3	[51;55[	6	0.0056	0.0014	0.0036 ¸ 0.0092
4	[55;59[	22	0.0208	0.0052	0.0092 ¸ 0.0300
5	[59;63[	52	0.0492	0.0123	0.0300 ¸ 0.0792
6	[63;67[	79	0.0744	0.0186	0.0792 ¸ 0.1536
7	[67;71[	118	0.1112	0.0278	0.1536 ¸ 0.2648
8	[71;75[	165	0.1556	0.0389	0.2648 ¸ 0.4204
9	[75;79[	186	0.1756	0.0439	0.4204 ¸ 0.5960
10	[79;83[	165	0.1556	0.0389	0.5960 ¸ 0.7516
11	[83;87[	103	0.0972	0.0243	0.7516 ¸ 0.8488
12	[87;91[	82	0.0772	0.0193	0.8488 ¸ 0.9260
13	[91;95[	45	0.0424	0.0106	0.9260 ¸ 0.9684
14	[95;97[	19	0.0180	0.0045	0.9684 ¸ 0.9864
15	[99;103[	11	0.0104	0.0026	0.9864 ¸ 0.9970
16	[103;107[	3	0.0021	0.0007	0.9970 ¸ 0.9999
	Сумма	1060	1	0.25	1

 

На основании этих результатов строим гистограмму и эмпирическую функцию распределения. Так как мы перешли от дискретной случайной величины к непрерывной, то мы считаем плотность вероятности постоянной внутри каждого интервала, а функция распределения на каждом интервале будет возрастать линейно от начального до конечного ее значения на интервале.

На рис. представлена гистограмма, которая почти симметрична относительно вертикали . Три центральных класса с наибольшими частотами (модальная группа) оказались точно симметричными (см. таблицу). Поэтому хорошей оценкой моды, медианы и математического ожидания будет значение . Огибающая гистограммы и сама гистограмма с ростом объема выборки будут приближаться к кривой нормального распределения (кривой Гаусса) с параметрами  и , то есть к кривой

 

.

 

Убеждаемся, что центральная предельная теорема выполняется.

На рис. представлена эмпирическая функция распределения — кумулята p_i. Эта функция приближенно выражается через функцию Лапласа (или интеграл вероятностей) :

 

,

 

по формуле

 

.

 

При  функция распределения F имеет точку перегиба ( ) и , то есть точка  является медианой.

 

4. Точечные оценки параметров распределения признака

 

Построение графиков эмпирических функций плотности вероятности гистограммы и функции распределения (кумяляты) дают общее представление о распределении случайной величины. Для уточнения деталей распределения по данным выборки статистики разработаны специальные методы. Очень помогают исследования, если удается определить тип закона распределения признака в генеральной совокупности (нормальный, биноминальный и др.). Очевидно, что благодаря центральной предельной теореме распределение генеральной совокупности часто является нормальным. И, следовательно, для уточнения модели остается точнее определить численные значения математического ожидания и дисперсии. Поэтому были точно рассчитаны распределения различных статистик для выборок из генеральной нормальной совокупности (c², Стьюдента, Фишера). Теория статистики, построена на расположении о нормальности исходного распределения, была первой. Ее можно назвать Гауссовской статистикой.

Раздел статистики, в которой изучается проблема получения информации о генеральной совокупности по выборочным данным, называется статистические выводы. Этот раздел можно разделить на два отдела: оценивания параметров и проверка гипотез.

Для оценивания параметра распределения можно использовать несколько выборочных статистик. Например, оценка генерального среднего может служить и выборное среднее 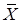, и медиана , и мода. Наилучшая оценка должна обладать такими свойствами как: несмещенность, эффективность и состоятельность. Для несмещенности необходимо, что бы выборочная статистика имела математическое ожидание равное оцениваемому параметру. Если имеется две несмещенные оценки, то из них следует выбирать ту, которая имеет меньшую выборочную дисперсию (она считается более эффективной). Оценка должна также быть состоятельной. Это означает, что с ростом объема выборки, дисперсия оценки должна стремится к нулю.

Иногда становится важным и такое свойство оценки как простота вычислений, малое время обработки. Можно выбрать такую оценку вместо более эффективной, но и более дорогой и длительной.

Обычно оценку случайний величины (статистику) обозначают большими латинскими буквами ( ), значение оценки из данных выборки – соответствующими малыми латинскими буквами ( ), действительное значение параметра генеральной совокупности — малыми буквами греческого алфавита ( ).

Признаки каждого объекта выборки объема n можно считать независимыми случайными величинами Х_i (i=1,2,…,n) имеющими одинаковые законы распределения (одинаковые параметры m и s). Точечной оценкой математического ожидания будет статистика

 

.

 

Случайную величину 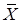 называют усредненным значением признака выборочным средним. Значение  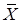для конкретной выборки будет среднее арифметическое из данных выборки

 

.

 

Если данные выборки сгруппировать в вариационный ряд, то  находят по формуле

 

,

 

где x_i — значение варианты для дискретного вариационного ряда или средина классового интервала для интервального вариационного ряда; m_i – частота варианта или классовая частота.

Точечной оценкой дисперсии s² признака, при неизвестной величине математического ожидания m является статистика

 

.

 

Значение этой статистики s² для конкретной выборки равно

 

.

 

Удобно пользоваться формулой

 

,

 

где  или .

Точечной оценкой стандартного отклонения (среднего квадратического отклонения) s является статистика

 

.

Точечной оценкой стандартного отклонения выборочной средней  будет статистика

 

 

Значение этой статистики для конкретной выборки равно

 

.

 

Подчеркнем, что s является характеристикой отдельного измерения, а  — характеристикой совокупности измерений.

Если данные выборки представлены интервальным вариационным рядом, то для большего объема n и малого числа классов k.

Оценка дисперсии признака является завышенной на величину , называемой поправкой Шеппарда с учетом этой поправки имеем

 

,

 

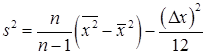где Dx — ширина классового интервала.

Если объем генеральной совокупности N, а объём выборки n соизмерим с N ( 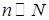), то дисперсия выборочной средней  рассчитывается по формуле

 

.

Рассмотрим пример. Результаты измерения признака Х из элементов выборки объёма  представлены интервальным вариационным рядом с :

 

№ интервала, i	Интервал	Середина интервала, xi	Частота, mi	mixi	mixi2
1	[76;85]	80	2	160	12800
2	[86;95]	90	5	450	40500
3	[96;105]	100	17	1700	170000
4	[106;115]	110	25	2750	302500
5	[116;125]	120	45	5400	648000
6	[126;135]	130	27	3510	456300
7	[136;145]	140	21	2940	411600
8	[146;155]	150	3	450	67500
9	[156;165]	160	1	160	25600
	Сумма		146	17520	2134800

 

По формуле находим выборочное среднее . Среднее от х² равно . Стандартные отклонение S находим с учетом поправки Шеппарда

 

 

Из расчета видно, что поправка Шеппарда незначительна. По формуле определяем стандартное отклонение выборочной средней .

Такие величины как выборочные мода и медиана также могут служить для оценки среднего генеральной совокупности (особенно если генеральное распределение симметрично). Разность выборочного среднего  и выборочной медианы (или моды) может быть оценкой коэффициента асимметрии. Статистики для моды и медианы определяются выборочными значениями. Например, для доли определенных элементов в генеральной совокупности (это вероятность Р случайно выбрать такой элемент) наилучшей точечной оценкой будет статистика  где Х число этих элементов в выборке n, то есть доля тех же элементов в выборке.

Для двухмерной случайной величины выборка объёма n состоит из последовательности n пар чисел . Точечной оценкой корреляционного момента является статистика

 

 

Для коэффициента корреляции точечной оценкой служит выражение

 

.

 

Для нахождения точечной оценки неизвестного параметра используется также метод наибольшего правдоподобия. Он состоит в том, что в качестве наиболее правдоподобного значения параметра Q берут то его значение Q, при котором вероятность получить в n опытах данную выборку  является максимально большой. Каждая из величин X_i имеет плотность вероятности . Функция правдоподобия определяется соотношением

 

.

 

Эта функция имеет максимум при , где  является решением управления

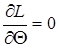 или .

 

Пусть  — выборка из распределения Пуассона . Тогда

 

_,

.

 

Уравнение для определения l имеет вид

 

,

 

решение которого даёт известный результат

математический дисперсия выборка дискретный

.