Интеграция детерминированных фракталов и хаос

Из рассмотренных примеров детерминистских фракталов можно увидеть, что они не проявляют никакого хаотического поведения и что они на самом деле очень даже предсказуемы. Как известно, теория хаоса использует фрактал для того, чтобы воссоздать или найти закономерности с целью предсказания поведения многих систем в природе, таких как, например, проблема миграции птиц.

Теперь давайте посмотрим, как это в действительности происходит. Используя фрактал, называемый Деревом Пифагора, не рассматриваемого здесь (который, кстати, не изобретен Пифагором и никак не связан с теоремой Пифагора) и Броуновского движения (которое хаотично), давайте попытаемся сделать имитацию реального дерева. Упорядочение листьев и веток на дереве довольно сложно и случайно и, вероятно не является чем-то достаточно простым, что может эмулировать короткая программа из 12 строк.

Для начала нужно сгенерировать Дерево Пифагора (Рисунок 4). Результат напоминает те старые детсадовские рисунки… Так что давайте сделаем ствол толще. На этой стадии Броуновское движение не используется. Вместо этого, каждый отрезок линии теперь стал линией симметрии прямоугольника, который становится стволом, и веток снаружи.

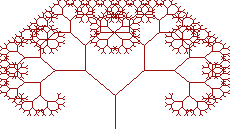
Рисунок 4. Дерево Пифагора

Но результат все еще выглядит слишком формальным и упорядоченным. Дерево еще не смотрится как живое. Попробуем применить некоторые из тех знаний в области детерминированных фракталов, которые мы только что приобрели.

Рисунок 5.

Теперь можно использовать Броуновское движение для создания некоторой случайной беспорядочности, которая изменяет числа, округляя их до двух разрядов. В оригинале были использованы 39 разрядные десятичные числа. Результат (слева) не выглядит как дерево. Вместо этого, он выглядит как хитроумный рыболовный крючок!

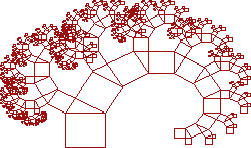
Рисунок 6.

Может быть округление до 2 разрядов было слишком уж много? Снова применяем Броуновское движение, округленное на этот раз до 7 разрядов. Результат по-прежнему выглядит как рыболовный крючок, но на этот раз в форме логарифмической спирали!

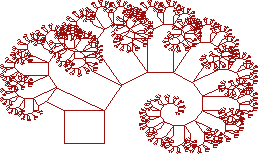
Рисунок 7.

Так как левая сторона (содержащая все нечетные числа) не производит эффект крючка, случайные беспорядочности, произведенные Броуновским движением применяются дважды ко всем числам с левой стороны и только один раз к числам справа. Может быть этого будет достаточно чтобы исключить или уменьшить эффект логарифмической спирали. Итак, числа округляются до 24 разрядов. На этот раз, результат - приятно выглядящая компьютеризированная хаотическая эмуляция реального дерева.

Рисунок 8.

Виды фракталов

Решётка Серпинского.

Это один из фракталов, с которыми экспериментировал Мандельброт, когда разрабатывал концепции фрактальных размерностей и итераций. Треугольники, сформированные соединением средних точек большего треугольника вырезаны из главного треугольника, образовывая треугольник, с большим количеством дырочек. В этом случае инициатор - большой треугольник а шаблон - операция вырезания треугольников, подобных большему. Так же можно получить и трехмерную версию треугольника, используя обыкновенный тетраэдр и вырезая маленькие тетраэдры. Размерность такого фрактала ln3/ln2 = 1.584962501.

Чтобы получить ковер Серпинского, возьмем квадрат, разделим его на девять квадратов, а средний вырежем. То же сделаем и с остальными, меньшими квадратами. В конце концов образуется плоская фрактальная сетка, не имеющая площади, но с бесконечными связями. В своей пространственной форме, губка Серпинского преобразуется в систему сквозных форм, в которой каждый сквозной элемент постоянно заменяется себе подобным. Эта структура очень похожа на разрез костной ткани. Когда-нибудь такие повторяющиеся структуры станут элементом строительных конструкций. Их статика и динамика, считает Мандельброт, заслуживает пристального изучения.

Рисунок 9. Решётка Серпинского.

Рисунок 10. Губка Серпинского.