Матричная игра как модель конкуренции

 и сотрудничества

Теория игр: совокупность математических методов, анализа и оценки поведения в конфликтных ситуациях, когда сталкиваются интересы двух или более сторон, преследующие различные, иногда противоположные цели. Противоречащие друг другу интересы наблюдаются в области экономики, военном деле, спорте, иногда противоречат интересы различных ступеней иерархии в СУ. Теория игр представляет собой математическую теорию конфликтных ситуаций. Ее цель-выработка рекомендаций по разумному поведению участников конфликта.

 

Постановка задачи:

Рассмотрим матричную игру двух лиц с нулевой суммой.

Задана матрица:

Участвуют 2 игрока. 1-ый выбирает номер строки, а 2-ой независимо от 1-го выбирает номер столбца. Если 1-ый загадал 2-ую строку, а второй – 2-ой столбец, то выигрыш второго составляет 8 рублей.

Вначале проведем анализ на доминирование. Так как строки выбирает первый игрок, то мы исключаем из платежной матрицы доминируемые строки. Первая строка доминирует третью. В результате исключения третьей строки получаем:

Первый и четвертый столбец равнозначны. Исключаем четвертый, у нас получается платежная матрица, которую упростить уже невозможно:

Далее проведем анализ игры на седловую точку. Найдем минимумы по строкам   и максимумы по столбцам :

   

 

 

Нижняя цена игры будет равна:   верхняя цена игры равна: .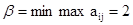

Поскольку , то решения игры в чистых стратегиях нет. Будем искать решение в смешанных стратегиях. Чтобы сделать все элементы платежной матрицы положительными, прибавим к каждому ее элементу константу, равную 10, при этом решение игры не  изменится, а цена игры  возрастет на 10 и будет больше нуля. Матрица игры примет следующий вид:

Решение игры сводится к нахождению решения симметричной пары взаимно двойственных задач линейного программирования. Пусть 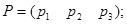 - стратегии игроков. Найдем сначала .

Проигрыш Второго игрока будет не больше, чем цена игры :

Разделим каждое из неравенств на  и введем обозначения , получим:

Поскольку , то переменные x ₁ , x ₂ , x ₃ , x ₄   удовлетворяют условию:

, но v   есть проигрыш второго игрока, который он стремится сделать минимальным. Следовательно, величина   должна быть максимальна. Таким образом, имеем следующую задачу линейного программирования:

Найти вектор , который обеспечивает максимум целевой функции , при следующих линейных ограничениях:

 

Решение:

Найдем ее оптимальное решение симплексным методом.

Итак, , при

Сначала приведем эту задачу к основной задаче линейного программирования:

Превратим неравенства в равенства, ля этого добавим к каждому неравенству дополнительные неотрицательные неизвестные x ₅ , x ₆ , x ₇ . Вспомогательная задача будет иметь вид:

 

, при ограничениях:

 

Откуда: ;

 

Составляем симплексную таблицу:

 

Ć	Б	Н	X1	X2	X3	X4	X5	X6	X7	Пояснения
0	X5	1	10	5	13	9	1	0	0	max ( D j >0)= 31 min (α)=1/17, x 3 в базис, x 6 из базиса
0	X6	1	14	2	17	0	0	1	0
0	X7	1	4	12	1	15	0	0	1
		3- S	28	19	31	13	0	0	0
0	X5	4/17	-12/17	59/17	0	9	1		0	max ( D j >0)= 24 min (α)= , x 4 в базис, x 5     - из
-1	X 3	1/17	14/17	2/17	1	0	0		0
0	X7	16/17	54/17	202/17	0	15	0		1
		20/17 -S	42/17	261/17	0	24	0		0
-1	X 4	4/153	-12/153	59/153	0	1			0	max ( D j >0)= 933/153 min (α)=4/59, x 2 в базис, x 4     - из
-1	X 3	1/17	14/17	2/17	1	0			0
0	X7	84/153	666/153	933/153	0	0			1
		84/153-S	666/153	933/153	0	0			0
-1	X2	4/59	-12/59	1	0	153/59			0	max ( D j >0)= 330/59 min (α)=8/330, x 1 в базис, x 7     - из
-1	X3	3/59	50/59	0	1	-18/59			0
0	X7	8/59	330/59	0	0	-933/59			1
		8/59-S	330/59	0	0	-933/59			0
-1	X2	24/330	0	1	0	666/330
-1	X3	10/330	0	0	1	690/330
-1	X1	8/330	1	0	0	-933/330
		0-S	0	0	0	0

 

;

Вернемся теперь к решению основной задачи, в целевую функцию входят решения:

Ć	Б	Н	X1	X2	X3	X4	Пояснения
-1	X 2	24/330	0	1	0	666/330
-1	X 3	10/330	0	0	1	690/330
-1	X 1	8/330	1	0	0	-933/330
		-42/330- K	0	0	0	-423/330

 

, тогда ;

Цена игры равна ; 

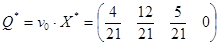
Найдем теперь оптимальную стратегию P ^* первого игрока. Выигрыш первого игрока будет не меньше, чем цена игры:

 

Разделим каждое из этих неравенств на   и введем обозначения . Получим:

           

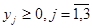
Поскольку , то

Но  есть выигрыш Первого игрока, который стремиться его максимизировать. Следовательно, величина   должна быть минимальна. Таким образом, имеем следующую задачу линейного программирования:

 Найти вектор , который обеспечивает минимум целевой функции 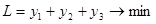, при следующих ограничениях:

           

Эта задача является двойственной по отношению к рассмотренной выше задаче.

Прямая задача:	Двойственная задача:

 

; ;

      ;

Т.к. x ₁ , x ₂ , x ₃ отличны от нуля:

; 

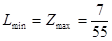, а цена игры по-прежнему равна ;

;

Теперь возвращаемся к исходной матрице игры . Решение игры принимает вид:

; ; ;

 

	q1=4/21	q2=12/21	q3=5/21	q4=0
p1=2/7	0	-5	3	-1
P2=3/14	4	-8	7	-10
P3=7/14	-6	2	-9	5

 

Найдем риск игры при использовании игроками своих оптимальных стратегий:

;

А также риск при использовании одним из игроков своей чистой, а другим – своей оптимальной стратегии (нижний индекс – Первого игрока, верхний – Второго):

; ;

; ;

; ;

; ;

; ;

; ;

; ;

Минимальное значение риска равно 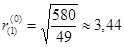  и меньше . Этот риск соответствует ситуации, когда первый игрок играет по своей чистой первой стратегии P ₁, а второй игрок использует оптимальную стратегию Q ^* .  Однако,играть с таким риском можно только с согласия обеих игроков, т.е. при их сотрудничестве друг с другом.

 

7. Анализ доходности и риска финансовых операций

Постановка задачи:

В реальной жизни мы имеем дело с финансовыми операциями. Финансовой называется операция, начальное и конечное состояния которой имеют денежную оценку и цель проведения которой заключается в максимизации дохода - разности между конечной и начальной оценками.

Почти всегда финансовые операции проводятся в условиях неопределенности и потому их результат невозможно предсказать заранее. Поэтому финансовые операции рискованны, т.е. при их проведении возможны как прибыль так и убыток (или не очень большая прибыль по сравнению с той, на что надеялись проводившие эту операцию).

Таким образом, любая финансовая операция должна быть оценена, по крайней мере, по двум показателям, а именно: доход – риск.

Предположим, что имеется несколько таких операций, каждая из которых характеризуется случайным доходом Q .

Средний ожидаемый доход `Q - это математическое ожидание с.в. Q: , где p_i есть вероятность получить доход q_i. А среднее квадратическое отклонение  - это мера разбросанности возможных значений дохода вокруг среднего ожидаемого дохода. Вполне разумно считать s количественной мерой риска операции и обозначить r. Дисперсия

D[Q] = M [(Q - `Q)<sup>2</sup>] = M [Q<sup>2</sup>] - `Q².

Рассмотрим четыре операции Q₁, Q₂, Q₃, Q_,4. Найдем средние ожидаемые доходы ` Q_i и риски r_i операций.

Ряды распределения, средние ожидаемые доходы и риски:

0	8	12	24
1/4	1/4	1/3	1/6

 

 

-6	-2	0	-6
1/4	1/4	1/3	1/6

 

 

0	2	4	16
1/3	1/3	1/6	1/6

 

 

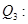
-6	-5	-4	3
1/3	1/3	1/6	1/6

 

; ; ;

 

; ; ;

 

 

; ; ;

 

; ; ;

 

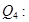
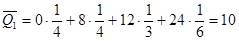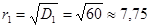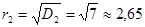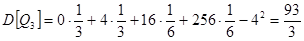Нанесем средние ожидаемые доходы `Q и риски  r на плоскость - доход откладываем по  горизонтали, а риски

r

по вертикали (см. рис.):

                                                                                                      

 

Получили 4 точки. Чем правее точка (`Q, r), тем более доходная операция, чем точка выше - тем более она рисковая. Значит, нужно выбирать точку правее и ниже. Точка (`Q¢, r¢) доминирует точку (`Q, r) если `Q¢ ³Q и r ¢ £ r. В нашем случае точка 2 доминирует точку 4.

Точка, не доминируемая никакой другой, называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Легко видеть, что если из рассмотренных операций надо выбирать лучшую, то ее обязательно надо выбрать из операций, оптимальных по Парето.

Найдем  лучшею операцию по формуле: j (Q)= 2 × Q - r , критерием оптимальности будет являться принцип максимизации результата для этого показателя, получаем:

j (Q₁)=2·10-7,75=12,25;

j (Q₂)=2· (-3)-2,65= -8,65;

j (Q₃)=2·4-5,54=2,46;

j (Q₄)= 2· (-23/6)-3,13≈ -10,8

Видно, что 1-ая операция – лучшая, а 4-ая – худшая. Таким образом точками, оптимальными по Парето являются точки: 1 и 3.