Выдвижение гипотезы о распределении случайной величины.

Министерство образования Российской Федерации

Московский государственный университет печати

Факультет полиграфической технологии

Дисциплина: Математика

Курсовая работа по теме:

«Статистические методы обработки

Экспериментальных данных»

Выполнил: студент

 Курс 2

 Группа ЗТПМ

 форма обучения заочная

Номер зачетной книжки Мз 023 н

Вариант № 13

Допущено к защите

Дата защиты

Результат защиты

Подпись преподавателя

Москва – 2010 год

 

0;3	3;6	6;9	9;12	12;15	15;18	18;21
4	6	9	11	14	18	13

 

21;24	24;27	27;30	30;33
11	7	4	3

 

1. Построение интервального и точечного статистических распределений результатов наблюдений. Построение полигона и гистограммы относительных частот.

 

 

i – порядковый номер;

I_i – интервал разбиения;

x_i – середина интервала I_i;

n_i – частота (количество результатов наблюдений, принадлежащих данному интервалу I_i);

w_i = 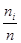 - относительная частота (n = 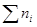- объём выборки);

H_i = 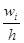 - плотность относительной частоты (h – шаг разбиения, т.е. длина интервала I_i).

 

i	Ii	xi	ni	wi	Hi
1 2 3 4 5 6 7 8 9 10 11	0;3 3;6 6;9 9;12 12;15 15;18 18;21 21;24 24;27 27;30 30;33	1,5 4,5 7,5 10,5 13,5 16,5 19,5 22,5 25,5 28,5 31,5	4 6 9 11 14 18 13 11 7 4 3	0,04 0,06 0,09 0,11 0,14 0,18 0,13 0,11 0,07 0,04 0,03	0,01 0,02 0,03 0,04 0,05 0,06 0,04 0,04 0,02 0,01 0,01

        

     Объём выборки:

         n = 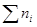=100,

          w_i = n_i/100;                                                                    

контроль: 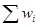=1

    Длина интервала                                                             

     разбиения (шаг):                                                             

              h = 3 ,                                                                  

           H_i =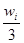

                             

 

                           å : 100 1,00                                                                                                                                                                   

                                                                                  

                                                                                                                                                                    

      Статистическим распределением называется соответствие между результатами наблюдений (измерений) и их частотами и относительными частотами. Интервальное распределение – это наборы троек (I_i ; n_i ; w_i) для всех номеров i, а точечное – наборы троек (x_i ; n_{i ;} w_i). Таким образом, в таблице имеются оба – и интервальное, и точечное - статистическое распределения.   

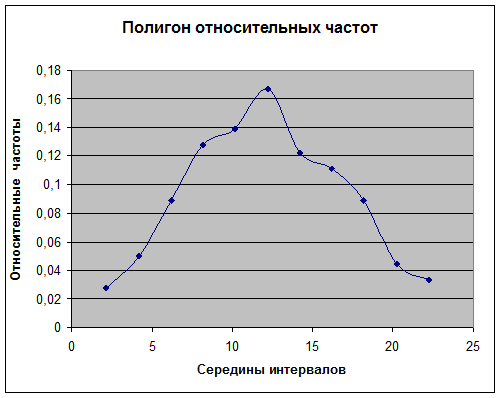
     Далее, строим полигон и гистограмму относительных частот.    

Полигон.

 

 Гистограмма.

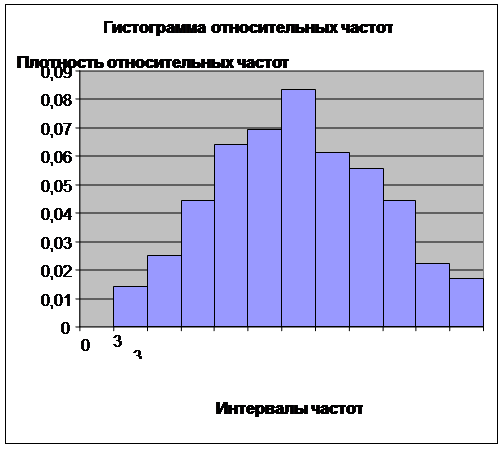
Полигон относительных частот – ломаная, отрезки которой последовательно (в порядке возрастания x_i) соединяют точки (x_i ; w_i). Гистограмма относительных частот – фигура, которая строится следующим образом: на каждом интервале I_i, как на основании, строится прямоугольник, площадь которого равна относительной частоте w_i; отсюда следует, что высота этого прямоугольника равна H_i = w_i/h – плотности относительной частоты. Полигон и гистограмма являются формами графического изображения статистического распределения.

Нахождение точечных оценок математического ожидания и     

дисперсии.

 

 

В качестве точечных оценок числовых характеристик изучаемой случайной величины используются:

- для математического ожидания

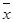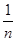
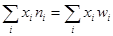                 =   (выборочная средняя),

- для дисперсии

                      s² = 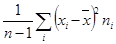 (исправленная выборочная),

где n – объём выборки, n_i – частота значения x_i .

     

Таким образом, в статистических расчетах используют приближенные равенства

 

                          MX » 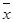   ,      DX » s² .

 

     Нахождение точечных оценок математического ожидания и дисперсии по данным варианта осуществим с помощью расчетной таблицы.

 

i	xi	ni	xi ni	(x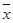i - )2 ni
1 2 3 4 5 6 7 8 9 10 11	1,5 4.5 7,5 10,5 13,5 16,5 19,5 22,5 25,5 28,5 31,5	4 6 9 11 14 18 13 11 7 4 3	6 27 67,5 115,5 189 297 253,5 247,5 178,5 114 94,5	829,44 779,76 635,04 320,76 80,64 6,48 168,48 479,16 645,12 635,04 744,12

                                                                           

                                                                       

  =  =

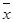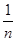
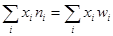х_in_i/100 = 1590/100= 15,9

                                                                            

     s² = =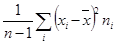

       =  5324,04/99=53,78

                                                                              

                                                              

                              

 

    å : 100   1590                5324,04

                                                             

Выдвижение гипотезы о распределении случайной величины.

 

    При выдвижении гипотезы (предположения) о законе распределения изучаемой случайной величины мы опираемся лишь на внешний вид статистического распределения. Т.е. будем руководствоваться тем, что профиль графика плотности теоретического распределения должен соответствовать профилю гистограммы: если середины верхних сторон прямоугольников, образующих гистограмму, соединить плавной кривой, то эта линия представляет в первом приближении график плотности распределения вероятностей.

     Итак, изобразим график и выпишем формулу плотности нормального (или гауссовского) распределения с параметрами а и 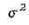, - ¥< а < + ¥,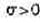

 

       Сравнение построенной гистограммы и графика плотности распределения приводит к следующему заключению о предполагаемом (теоретическом) законе распределения в рассматриваемом варианте исходных данных:

Вариант 13 – нормальное (или гауссовское распределение)