Параллелограммы периодов

Чтобы дать геометрическое истолкование двоякой периодичности, рассмотрим в плоскости комплексного переменного четыре точки

 

 

считая  произвольным комплексным числом.

Так как отношение  есть мнимое число, то эти четыре точки изображают вершины некоторого параллелограмма P.

Полагая

,

 

мы видим, что четыре точки, упомянутые выше, есть вершины параллелограмма , который может быть получен из основного параллелограмма  посредством некоторого сдвига.

Придавая m и n всевозможные целые значения, мы получим сеть параллелограммов , конгруэнтных между собой и покрывающих всю плоскость (рис. 1).

Чтобы любые два параллелограмма нашей сети не имели общих точек, условимся причислять к каждому параллелограмму  лишь часть его границы, а именно стороны

 

,

,

 

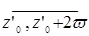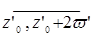за исключением концов

 

 

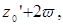
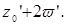
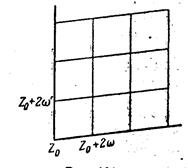
Рисунок 1 – Сеть параллелограммов

Что же касается двух сторон параллелограмма 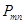, мы их будем рассматривать принадлежащими к смежным параллелограммам с 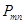. Тогда любая точка плоскости принадлежит одному и только одному из этих параллелограммов, например .

Точки вида

 

,

 

где 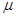 и 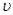 - любые целые числа, называются конгруэнтными или эквивалентными с точкой z; в параллелограммах  они занимают то же положение, что и точка z в .

Среди этих эквивалентных точек имеется одна точка, которая принадлежит основному параллелограмму P (эта точка .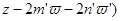

Итак, можно сказать, что всякая точка плоскости эквивалентна некоторой и притом единственной точке основного параллелограмма Р. Будем называть параллелограммы параллелограммами периодов; выбор среди них основного параллелограмма Р, очевидно, произволен. Теперь можно геометрически истолковать соотношение (2). Они выражают, что функция f ( z ) принимает одно и то же значение во всех эквивалентных точках. Следовательно, достаточно изучить эллиптическую функцию в одном из параллелограммов, чтобы знать ее поведение во всей плоскости.

 

Основные теоремы

Теорема 1. Производная эллиптической функции есть также функция эллиптическая. В самом деле, дифференцируя соотношение (1), имеющее место при любом z, получаем

 

Таким образом, производная f ’( z ) имеет те же периоды 2 и 2 , что и первоначальная функция. С другой стороны, будучи однозначной, как и f ( z ), f ’( z ) не может иметь на конечном расстоянии других особых точек, кроме полюсов, так как если f ( z ) голоморфна в некоторой точке, то производная f ’( z ) тоже голоморфна в этой точке, а если f ( z ) имеет полюс в некоторой точке, то и f ’( z ) будет иметь полюс в этой точке. Следовательно, f ’( z ) есть мероморфная функция, допускающая два периода 2 и 2 , и согласно определению она будет эллиптической функцией с теми же периодами, что и первоначальная функция.

Теорема 2. Эллиптическая функция, отличная от постоянного, имеет по крайней мере один полюс в параллелограмме периодов.

Действительно, допуская противное, мы имели бы целую функцию, отличную от постоянного. Ее параллелограмм периодов есть ограниченная часть плоскости и в этой области, включая ее границу, наша функция голоморфна, а значит, и подавно непрерывна, а потому и ограничена. Следовательно, существует такое положительное число М, что во всем основном параллелограмме периодов имеем

 

 

Так как во всех остальных параллелограммах сети значения функции  повторяются, то неравенство |f ( z )|<M будет справедливо для всех точек z плоскости. Итак, мы имеем целую функцию f ( z ) ограниченную во всей плоскости. Согласно теореме Лиувилля отсюда заключаем, что f ( z ) приводится к постоянному. Полученное противоречие убеждает нас в справедливости теоремы.

Следствия

1 Если две эллиптические функции с одинаковыми периодами имеют в параллелограмме периодов одни и те же полюсы с одинаковыми главными частями, то они отличаются лишь постоянным слагаемым.

В самом деле, положим, что  и  две эллиптические функции с одинаковыми периодами 2 и 2 , имеющие в параллелограмме периодов одни и те же полюсы с одинаковыми главными частями. Тогда их разность - будет двоякопериодической функцией с периодами 2 и 2 , без полюсов, а значит, по доказанной теореме эта разность равняется тождественно постоянному.

2 Если две эллиптические функции с одинаковыми периодами имеют в параллелограмме периодов одинаковые нули и полюсы одной и той же кратности, то они отличаются лишь постоянным множителем.

Действительно, положим, что  и  две эллиптические функции с одинаковыми периодами 2 и 2 , имеющие в параллелограмме периодов одинаковые нули и полюсы одной и той же кратности.

Тогда их отношение  представляет двоякопериодическую функцию с периодами 2 и 2 , причем это отношение не имеет полюсов. Следовательно, по доказанной теореме это отношение равно тождественно постоянному.

Теорема 3. Сумма вычетов эллиптической функции относительно всех полюсов, расположенных в параллелограмме периодов, равна нулю.

Прежде всего заметим, что если на границе параллелограмма периодов имеются полюсы эллиптической функции, то мы можем немного сдвинуть этот параллелограмм так, чтобы все полюсы, расположенные на первоначальном параллелограмме периодов, оказались бы внутри сдвинутого параллелограмма. Обозначим вершины этого параллелограмма через

 

 

на его сторонах нет полюсов функции f ( z ). Согласно общей теореме о вычетах мы получим сумму вычетов S относительно всех полюсов, лежащих внутри параллелограмма, если вычислим интеграл , распространив его на периметр этого параллелограмма, проходимый в положительном направлении. Таким образом, имеем

 

 (3)

 

где все интегрирования совершаются по прямолинейным отрезкам, соединяющим указанные точки. Объединяя первый и третий интегралы, делаем в этом последнем подстановку

 

 

и пользуясь периодичностью, находим

 

 

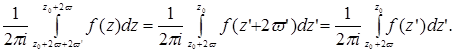
Таким образом, сумма первого и третьего интегралов выражения (3), равная

 

 

есть нуль потому, что интегрирования совершаются по одному и тому же отрезку в противоположных направлениях.

То же самое можно утверждать относительно суммы второго и четвертого интегралов, если в первом интеграле совершить подстановку

 

.

 

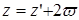Возвращаясь к формуле (3), мы убеждаемся, что S равно нулю.

Теорема 4. Эллиптическая функция принимает в параллелограмме периодов всякое значение (конечное или бесконечность) одинаковое число раз. Пусть  - произвольное комплексное число. Покажем, что число корней уравнения

 

 

 

лежащих в параллелограмме периодов, совпадает с числом полюсов функции f ( z ), расположенных в этом параллелограмме. Само собой разумеется, что при счете числа нулей функции

 

f ( z ) -  

 

или ее полюсов мы каждый нуль или полюс считаем столько раз, какова его кратность. Для доказательства нашего утверждения прежде всего заметим, что если на границе параллелограмма периодов имеются нули или полюсы функции

 

f ( z ) - ,

 

то мы можем немного сдвинуть этот параллелограмм так, чтобы все нули и полюсы, расположенные на первоначальном параллелограмме периодов, оказались бы внутри сдвинутого параллелограмма.

Обозначим вершины этого параллелограмма через

 

 

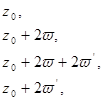
на его сторонах нет нулей и полюсов функции

 

f ( z ) -  .

 

Образуем вспомогательную функцию

 

 

которая будет эллиптической с периодам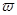и 2 и 2 , причем на сторонах рассматриваемого параллелограмма периодов она не будет иметь полюсов.

Применяя к этой функции предыдущую теорему 3, мы имеем:

 

 (4)

 

где интегрирование распространено в положительном направлении по контуру упомянутого параллелограмма. С другой стороны, как известно, интеграл

 

 

изображает разность между числом нулей и полюсов функции

 

f ( z ) - ,

лежащих внутри контура интегрирования.

Так как согласно формуле (4) этот интеграл равен нулю, то, следовательно, число корней уравнения

 

 

лежащих внутри параллелограмма периодов, совпадает с числом полюсов функции f ( z ), расположенных внутри того же параллелограмма. Таким образом, теорема доказана.

Если f ( z ) принимает в параллелограмме периодов всякое значение s раз, то она называется эллиптической функцией порядка s.

В силу теоремы 3 не может существовать эллиптической функции, имеющей в параллелограмме периодов один простой полюс. Таким образом, s всегда не меньше двух, т. е. не существует эллиптических функций первого порядка. В дальнейшем мы фактически построим эллиптические функции второго порядка. Существуют, конечно, и эллиптические функции более высокого порядка.

Теорема 5. Разность между суммой всех нулей и суммой всех полюсов эллиптической функции, расположенных в параллелограмме периодов, равна некоторому ее периоду, т. е.

 

,

 

где  - нули, а  - полюсы, расположенные в параллелограмме периодов. Само собой понятно, что при образовании суммы нулей или суммы полюсов

каждый нуль или полюс нужно повторить слагаемым столько раз, какова его кратность. Для доказательства прежде всего заметим, что если на границе параллелограмма периодов имеются нули или полюсы эллиптической функции, то путем небольшого сдвига этого параллелограмма мы можем достигнуть того, чтобы все нули и полюсы, расположенные на первоначальном параллелограмме периодов, попали бы внутрь сдвинутого параллелограмма. Обозначим через

 

 

вершины этого параллелограмма. На его сторонах нет нулей и полюсов функции f (z). Тогда, как известно, искомая разность между суммами всех нулей и полюсов, расположенных внутри упомянутого параллелограмма, изображается в виде интеграла

 

где интегрирование совершается по периметру параллелограмма в положительном направлении. Таким образом, имеем

 

 (5)

 

При интегрировании вдоль периметра параллелограмма сумма

 

 

приводится посредством перемены во втором интеграле z на  и

использования периодичности к следующему выражению

 

 

так как

 

,

 

то число в скобке есть нуль или вида

 

 

где  - целое. Таким образом, сумма двух рассматриваемых интегралов вообще равна  Аналогично сумма двух остальных интегралов

 

 

приводится посредством того же рассуждения к  Возвращаясь к формуле (5), перепишем ее в виде

 

 

что и требовалось доказать.

Примечание - применяя доказанную теорему к функции

 

f ( z ) - ,

 

где  - произвольное комплексное число, мы видим, что сумма корней уравнения

 

 

расположенных в параллелограмме периодов, конгруэнтна с суммой полюсов функции f ( z ), лежащих в этом параллелограмме, относительно ее первоначальных периодов 2 и 2 .