Возможные обобщения теоремы

Познакомимся с некоторыми способами обобщения, которые будем иллюстрировать утверждениями и задачами.

1. Обобщение по размерности. Известно следующее утверждение:

Если , то для любой точки  существуют такие числа  и , что

 и .

Пользуясь обобщением по размерности, приходим к утверждению:

Если  лежит в плоскости , то для любой точки  найдутся такие числа , , , 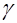что

 и .

2. Обобщение путем отбрасывания условий. Данный способ особенно эффективен при решении задач. В частности, он используется тогда, когда не удается решить какую-либо задачу. С этой целью мы отбрасываем какое-либо условие или заменяем его на более слабое, а потом решаем новую задачу:

Доказать, что при    выполняется неравенство

.

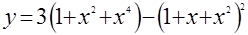Здесь может быть отброшено условие . Тогда, введя функцию  при 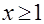 и используя производную, легко устанавливаем, что  при .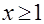

3. Обобщение на основе рассмотрения частных случаев. Этот метод особенно эффективен в том случае, если желательно угадать ответ. Рассмотрим известный пример:

Найти , если .

Обращаемся к частным случаям:

Это позволяет обобщить утверждение, высказав гипотезу, что 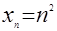, а потом ее и доказать.

4. Обобщение на основе метода доказательства.  В ходе поиска решения задачи или доказательства теоремы мы нашли нужный метод. Анализируя метод, выясним, что он может быть использован в более общей ситуации. Это позволяет сформулировать и доказать обобщение утверждения.

Известна задача: Если в параллелограмме соединить середины смежных сторон, то полученный четырехугольник – параллелограмм.

Анализируя метод доказательства, можно получить известное обобщение.

5. Обобщение путем изменения. Анализируя объекты, которые входят в известное утверждение, заменяем их на другие и пытаемся сформулировать и доказать обобщения.

Обратимся к теореме Виета. В условии речь идет о трехчлене . Что можно менять? Это зависит от человека, который пытается обобщать, а точнее, какие объекты он увидит. Дело это творческое, и не существует единого рецепта. Обратимся к записи, где выделена часть объектов, которые могут быть изменены:

Без труда можно сформулировать возможные обобщения.

6. Обобщение как усиление. Этот метод поясняем на примере доказательства неравенства

.

Введем функцию . Легко убедиться, что при  она возрастает и график является выпуклым вниз (рис. 1).

рис. 1

Рассмотрим криволинейную трапецию . Очевидно, что ее площадь  может быть вычислена по формуле

.

Площадь криволинейного треугольника  находится по формуле

, или .

Отсюда ясно, что в условии предлагается доказать, что

.

Так как площадь квадрата  равна , то достаточно убедиться, что площадь криволинейного треугольника  меньше . Укажем координаты “нужных” точек:

.

Теперь рассмотрим точку . Пользуясь выпуклостью вниз графика функции , легко убедиться, что площадь криволинейного треугольника  меньше площади треугольника . Докажем неравенство  (это больше, чем нам нужно):

.

Отсюда и получаем требуемое неравенство.

7. Обобщение на основе соединения. При данном способе обобщения новые утверждения получаются путем рассмотрения свойств объектов из разных тем (отметим, что этот метод отражен в названии наук – биофизика, биохимия, математическая биология и др.).

Известны следующие утверждения:

1. а) Если  и  - корни трехчлена , то .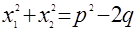

б) Если  и  - любые числа, а , , то  и  - корни уравнения .

2. Пусть  - точка касания вписанной в прямоугольный треугольник окружности с гипотенузой  и ,  (рис. 2). Доказать, что площадь треугольника равна .

рис. 2

Соединяя эти утверждения, можем сформулировать следующие задания:

Если  и  - отрезки, на которые точка касания окружности, вписанной в прямоугольный треугольник, разбивает гипотенузу, то:

а) ;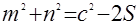

б) ;

в) ,

где  - гипотенуза, а  - площадь треугольника.