 |
Главная |
Урок на тему «Иррациональные уравнения» (10 класс)
|
из
5.00
|
Цель: обобщить и систематизировать способы решения иррациональных уравнений и умения применять их в различных ситуациях.
Основными методами решения иррациональных уравнений являются:
1) метод возведения обеих частей уравнения в одну и ту же степень, т. е. замена уравнения  уравнением
уравнением  ;
;
2) метод введения новой переменной.
Однако зачастую иррациональные уравнения решаются с помощью рассуждений, основанных на анализе структуры уравнения, путем установления множества допустимых значений неизвестного, извлечения корня  -ной степени из степени с показателем
-ной степени из степени с показателем  , на основе теорем равносильности. Отметим и то, что иррациональные уравнения могут содержать один, два и больше корней, причем они могут быть одной степени или разных степеней. Проиллюстрируем сказанное конкретными примерами.
, на основе теорем равносильности. Отметим и то, что иррациональные уравнения могут содержать один, два и больше корней, причем они могут быть одной степени или разных степеней. Проиллюстрируем сказанное конкретными примерами.
1. Решите уравнения:
а)  ;
;
б)  ;
;
в)  .
.
Исследование структуры уравнения а) показывает, что оно не имеет корней, так как  , и потому
, и потому 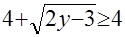 ; в случае б) имеем
; в случае б) имеем  при допустимых значениях
при допустимых значениях  и
и  . Анализ структуры уравнения в) показывает, что его решением является каждое значение
. Анализ структуры уравнения в) показывает, что его решением является каждое значение 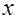 , для которого одновременно
, для которого одновременно  и
и  . Этому требованию удовлетворяет
. Этому требованию удовлетворяет 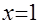 .
.
2. Решите уравнения:
а)  ;
;
б)  .
.
Подкоренные выражения просты, поэтому целесообразно, прежде всего, выявить множество допустимых значений неизвестного. Легко установить, что область определения уравнения а) – пустое множество, а потому уравнение не имеет решений. В случае б) уравнение может иметь решение при  , т. е. при
, т. е. при  . Учитывая, что левая часть уравнения имеет смысл при
. Учитывая, что левая часть уравнения имеет смысл при  , получаем, что уравнение имеет единственный корень:
, получаем, что уравнение имеет единственный корень:  .
.
3. Решите уравнения:
а)  ;
;
б)  .
.
Уравнения а) и б) можно записать соответственно в виде:
а)  ;
;
б)  ,
,
которые, в свою очередь, равносильны уравнениям:
а)  ;
;
б)  .
.
Решим уравнение б), для чего воспользуемся методом интервалов:
1) при  уравнение
уравнение  равносильно уравнению
равносильно уравнению  , корнем которого является
, корнем которого является 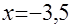 ;
;
2) если  , то исходное уравнение равносильно уравнению
, то исходное уравнение равносильно уравнению  или
или 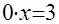 , которое не имеет решений;
, которое не имеет решений;
3) при  уравнение
уравнение  преобразуется в уравнение
преобразуется в уравнение  , или
, или  , откуда
, откуда  .
.
Часто решение иррациональных уравнений основывается на возведении обеих частей уравнения в одну и ту же степень. Рассмотрим, например, решение уравнения  . Запишем данное уравнение в виде
. Запишем данное уравнение в виде  и возведем обе его части в квадрат. Получим
и возведем обе его части в квадрат. Получим
 ,
,
 ,
,  ,
,
 .
.
Так как при возведении обеих частей уравнения в одну и ту же степень возможно появление посторонних корней, то обязательна проверка найденных корней. Число  удовлетворяет исходному уравнению, а число
удовлетворяет исходному уравнению, а число  нет.
нет.
Уравнение  можно решить с применением теорем равносильности. Известно, что уравнение
можно решить с применением теорем равносильности. Известно, что уравнение 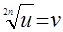 равносильно системе
равносильно системе

Заданное уравнение равносильно системе 
которая имеет единственное решение  .
.
К решению исходного уравнения можно было бы применить и метод введения новой переменной. Запишем данное уравнение в виде 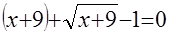 . Положив
. Положив  , получаем
, получаем  . Продолжение решения не вызывает трудностей.
. Продолжение решения не вызывает трудностей.
Рассмотрим еще пример уравнения, содержащего квадратные, кубические и другие корни.
Решите уравнения:
а)  ;
;
б)  .
.
Положив в уравнении а)  и
и  , приходим к системе уравнений
, приходим к системе уравнений  и
и  , откуда
, откуда  ,
,  ;
;  ,
,  ;
;  ,
,  .
.
Подставив в одно из равенств значения  или
или  , получим
, получим  ,
,  ,
,  .
.
Область допустимых значений уравнения б) такова: 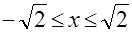 . Если
. Если  - корень уравнения, то
- корень уравнения, то  , или
, или 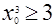 . Но
. Но  , следовательно, уравнение б) не имеет решений.
, следовательно, уравнение б) не имеет решений.
Систематизация и обобщение указанных способов решения иррациональных уравнений и составляет содержание рассматриваемого урока. Осуществляется она в процессе выполнения следующих упражнений:
1. Назовите, какие из данных уравнений иррациональные:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) 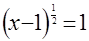 ;
;
е)  .
.
Иррациональные уравнения, содержащие только квадратные корни.
I. Уравнения, решаемые с помощью анализа структуры уравнения.
2. Решите каждое из уравнений:
а)  ;
;
б)  .
.
II. Уравнения, решаемые установлением множества допустимых значений неизвестного.
3. Решите уравнения:
а) 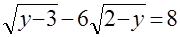 ;
;
б)  .
.
III. Уравнения, решаемые с помощью извлечения квадратного корня.
4. Решите уравнения:
а)  ;
;
б)  .
.
IV. Уравнения, решаемые с помощью теорем равносильности.
5. Дано уравнение  . Почему и где в нижеуказанных в связи с его решением рассуждениях «потерян» корень?
. Почему и где в нижеуказанных в связи с его решением рассуждениях «потерян» корень?
 ,
,
 ,
,
 ,
,  ,
,  ,
,
 ,
,  ,
,
 ,
,  . Решений нет.
. Решений нет.
Найдите «потерянный» корень.
6. Дано уравнение  . Прокомментируйте следующие его решения:
. Прокомментируйте следующие его решения:
а)  ,
, 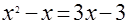 ,
, 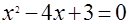 ,
,  ,
,  ;
;
б)  ,
,  ,
,  .
.
а.  ,
,  ,
,  ,
, 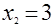 ;
;
б.  ,
,  ,
,  ,
,  .
.
V. Уравнения, содержащие один корень.
7. Решите уравнения:
а)  ;
;
б)  .
.
VI. Уравнения, содержащие два корня.
8. Решите уравнения:
а)  ;
;
б)  .
.
Иррациональные уравнения, содержащие квадратные, кубические и другие корни.
9. Решите уравнения:
а)  ;
;
б)  .
.
Учитывая сложность темы «Иррациональные уравнения», для обобщающего урока целесообразно планировать сдвоенный урок. Формы выполнения упражнений могут быть различны: выполнение упражнений у доски, комментированное решение, самостоятельная работа и т. д.
ЗАКЛЮЧЕНИЕ
Следует отметить, что включение учащихся в деятельность по отысканию обобщений математических фактов играет большую роль в воспитании качеств творческой личности. При этом ученики учатся самостоятельно ставить и решать новые для них задачи, учатся продуктивному умственному труду. Кроме того, такая деятельность способствует лучшему усвоению знаний, обнаружению связей между ними, учит рассматривать определенные факты, закономерности с более общей точки зрения, с позиции общих закономерностей, что чрезвычайно важно при изучении математики.
ЛИТЕРАТУРА.
1. Саранцев Г. И. «Упражнения в обучении математике». – М.: Просвещение, 1995.
2. Саранцев Г. И. «Общая методика преподавания математики» - М.: Просвещение, 1999.
3. Оганесян В. А., Колягин Ю.М., Луканкин Г. Л., Саннинский В. Я. «Методика преподавания математики в средней школе». – М.: Педагогика, 1976.
4. Пойа Д. «Как решать задачу?».
5. Зильберберг Н. И. «Урок математики. Подготовка и проведение». – М.: Просвещение, 1996.
6. Епишева О. Б., Крупич В. И. «Учить школьников учиться математике».
7. Пичурин Л. Ф. «Воспитание учащихся при обучении математике».
|
из
5.00
|
Обсуждение в статье: Урок на тему «Иррациональные уравнения» (10 класс) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

