Периодизации здоровья населения в России с помощью метода корреляционных плеяд.

Как уже рассматривалось в теории метод корреляционных плеяд можно построить как по матрице коэффициентов корреляции ,так и по матрице расстояния. В данном случае этот метод будет выполнятся по матрице расстояний.

В матрице расстояний выбирается минимальное по абсолютной величине расстояние(за исключением диагонального).Минимальное расстояние оказалось между 14 и 15 (0,133). Соединяем эти два элемента - это соответствует шагу 1. Рассматриваем 14 столбец и выбираем в этом столбце минимальное значение кроме 0,133 (14-13(0,386))и рассматриваем 15-й столбец (15-13(0,454)). Из двух этих значений выбираем минимальное(т.е 0,386 и соединяем 13 и 14 ) это соответствует шагу 2. Процесс продолжается до полного исчерпания объектов множества. В данном случае до полного исчерпания 15 объектов. Весь алгоритм представлен в таблице 9.

Таблица 9

шаг	рассматриваемые столбцы	уже выбранные значения	минимальное значение кроме выбранных	соединяем элементы
21	5	0,378 ;0,431; 0,919 ; 0,729	5-10(0,802)	6 и 10
	6	0,648 ;0,639 ;0,729	6-10(0,646)
22	6	0,421; 0,439;0,648 ; 0,639;0,729 ; 0,646	6-11(0,773)	10 и 12
	10	0,182; 0,461 ;0,646	10-12(0,579)
23	10	0,182; 0,461 ;0,646 ; 0,579	10-5(0,802)	12 и 14
	12	0,253 ;0,408 ;0,579	12-14(0,510)
24	12	0,253 ;0,408 ;0,579; 0,510	12-15(0,559)	12 и 15
	14	0,133 ;0,386; 0,510	14-11(0,779)
25	12	0,253 ;0,408 ;0,579; 0,510; 0,559	12-9(0,997)	15 и 13
	15	0,133; 0,559	15-13(0,454)
26	15	0,133; 0,559; 0,454	15-11(0,805)	13 и 11
	13	0,386 ;0,253; 0,454	13-11(0,652)
27	13	0,386 ;0,253; 0,454; 0,652	13-10(0,827)	11 и 6
	11	0,408 ;0,182;0,611; 0,652	11-6(0,773)
28	11	0,408 ;0,182;0,611; 0,652; 0,773	11-14(0,779)	11 и 14
	6	0,648 ;0,639 ;0,729 ; 0,646; 0,773	6-12(1,096)
29	11	0,408 ;0,182;0,611; 0,652; 0,773;0,779	11-15(0,805)	11 и 15
	14	0,133 ;0,386; 0,510; 0,779	14-10(0,956)
30	11	0,408 ;0,182;0,611; 0,652; 0,773;0,779; 0,805	11-5(0,881)	11 и 5
	15	0,133; 0,559; 0,454; 0,805	15-10(0,981)
31	11	0,408 ;0,182;0,611; 0,652; 0,773;0,779; 0,805; 0,881	11-7(0,993)	5 и 10
	5	0,378 ;0,431; 0,919 ; 0,729;0,881	5-10(0,802)
32	5	0,378 ;0,431; 0,919 ; 0,729;0,881;0,802	5-12(1,037)	10 и 13
	10	0,182; 0,461 ;0,646 ; 0,579; 0,802	10-13(0,827)
33	10	0,182; 0,461 ;0,646 ; 0,579; 0,802; 0,827	10-7(0,879)	10 и 7
	13	0,386 ;0,253; 0,454; 0,652;0,827	13-5(1,212)
34	10	0,182; 0,461 ;0,646 ; 0,579; 0,802; 0,827;0,879	10-14(0,956)	10 и 14
	7	0,439 ;0,261 ;0,500;0,879	7-11(0,993)

шаг	рассматриваемые столбцы	уже выбранные значения	минимальное значение кроме выбранных	соединяем элементы
1	14 и 15	-	0,133	14 и 15
2	14	0,133	14-13(0,386)	14 и 13
	15	0,133	15-13(0,454)
3	14	0,133 ;0,386	14-12(0,510)	13 и 12
	13	0,386	13-12(0,253)
4	13	0,386 ;0,253	13-15(0,454)	12 и 11
	12	0,253	12-11(0,408)
5	12	0,253 ;0,408	12-14(0,510)	11 и 10
	11	0,408	11-10(0,182)
6	11	0,408 ;0,182	11-9(0,611)	10 и 9
	10	0,182	10-9(0,461)
7	10	0,182; 0,461	10-12(0,579)	9 и 6
	9	0,461	9-6(0,421)
8	9	0,461; 0,421	9-7(0,500)	6 и 7
	6	0,421	6-7(0,439)
9	6	0,421; 0,439	6-3(0,639)	7 и 8
	7	0,439	7-8(0,261)
10	7	0,439; 0,261	7-9(0,500)	7 и 9
	8	0,261	8-9(0,647)
11	7	0,439 ;0,261 ;0,500	7-10(0,879)	9 и 11
	9	0,461; 0,421;0,500	9-11(0,611)
12	9	0,461; 0,421;0,500 ; 0,611	9-8(0,647)	9и 8
	11	0,408 ;0,182;0,611	11-13(0,652)
13	9	0,461; 0,421;0,500 ; 0,611;0,647	9-3(0,916)	8 и 6
	8	0,261;0,647	8-6(0,648)
14	8	0,261;0,647 ;0,648	8-10(0,992)	6 и 3
	6	0,421; 0,439;0,648	6-3(0,639)
15	6	0,421; 0,439;0,648 ;0,639	6-10(0,646)	3 и 5
	3	0,639	3-5(0,378)
16	3	0,639 ;0,378	3-4(0,700)	5 и 4
	5	0,378	5-4(0,431)
17	5	0,378 ;0,431	5-6(0,729)	4 и 3
	4	0,431	4-3(0,700)
18	4	0,431 ;0,700	4-10(1,068)	3 и 9
	3	0,639 ;0,378;0,700	3-9(0,916)
19	3	0,639 ;0,378;0,700 ; 0,916	3-10(0,972)	9 и 5
	9	0,461; 0,421;0,500 ; 0,611;0,647 ; 0,916	9-5(0,919)
20	9	0,461; 0,421;0,500 ; 0,611;0,647; 0,916; 0,919	9-12(0,997)	5 и 6
	5	0,378 ;0,431; 0,919	5-6(0,729)

Вспомогательная таблица для построения древа .

 

шаг	рассматриваемые столбцы	уже выбранные значения	минимальное значение кроме выбранных	соединяем элементы
41	11	0,408 ;0,182;0,611; 0,652; 0,773;0,779; 0,805; 0,881; 1,104; 0,993	11-8(1,074)	7 и 3
	7	0,439 ;0,261 ;0,500; 0,879; 0,993	7-3(1,032)
42	7	0,439 ;0,261 ;0,500; 0,879; 0,993;1,032	7-5(1,164)	3 и 11
	3	0,639 ;0,378;0,700 ; 0,916; 0,972; 1,032	3-11(1,075)
43	3	0,639 ;0,378;0,700 ; 0,916; 0,972; 1,032;1,075	3-8(1,233)	11 и 8
	11	0,408 ;0,182;0,611; 0,652; 0,773;0,779; 0,805; 0,881; 1,104; 0,993; 1,075	11-8(1,074)
44	11	0,408 ;0,182;0,611; 0,652; 0,773;0,779; 0,805; 0,881; 1,104; 0,993; 1,075; 1,074	11-2(1,964)	8 и 2
	8	0,261;0,647; 0,648; 0,992; 1,074	8-2(1,154)
45	8	0,261;0,647; 0,648; 0,992; 1,074; 1,154	8-3(1,233)	2 и 1
	2	1,154	2-1(0,183)

шаг	рассматриваемые столбцы	уже выбранные значения	минимальное значение кроме выбранных	соединяем элементы
35	10	0,182; 0,461 ;0,646; 0,579; 0,802; 0,827;0,879; 0,956	10-15(0,981)	10 и 14
	14	0,133 ;0,386; 0,510; 0,779;0,956	14-9(1,299)
36	10	0,182; 0,461 ;0,646; 0,579; 0,802;0,827; 0,879; 0,956;0,981	10-3(0,972)	10 и 3
	15	0,133; 0,559; 0,454; 0,805; 0,981	15-9(1,324)
37	10	0,182; 0,461 ;0,646; 0,579; 0,802;0,827; 0,879; 0,956;0,981; 0,972	10-8(0,992)	10 и 8
	3	0,639 ;0,378;0,700 ; 0,916; 0,972	3-7(1,032)
38	10	0,182; 0,461 ;0,646; 0,579; 0,802;0,827; 0,879; 0,956;0,981; 0,972;0,992	10-4(1,068)	10 и 4
	8	0,261;0,647; 0,648; 0,992	8-11(1,074)
39	10	0,182; 0,461 ;0,646; 0,579; 0,802;0,827; 0,879; 0,956;0,981; 0,972;0,992; 1,068	10-2(1,915)	4 и 11
	4	0,431 ;0,700;1,068	4-11(1,104)
40	4	0,431 ;0,700;1,068; 1,104	4-12(1,140)	11 и 7
	11	0,408 ;0,182;0,611; 0,652; 0,773;0,779; 0,805; 0,881; 1,104	11-7(0,993)

 

Результатом этих действий выступает построение древа. Данное древо изображено на рисунке 3,8.

 

 

 

 

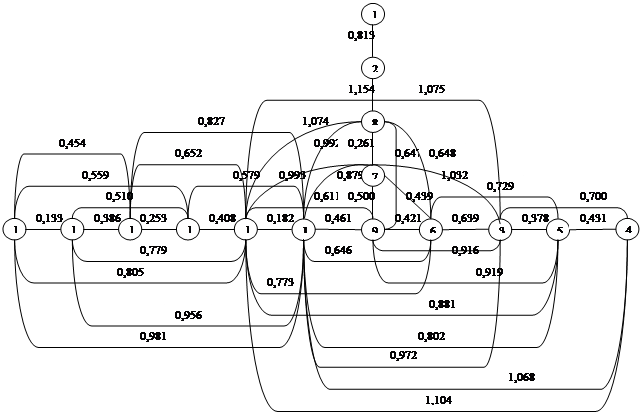
Рис.3,8 Древо взаимосвязей

Из рисунка видно, что этот метод учел все связи объектов, а не отбросил как два предыдущих «ненужную» информацию и больше всего связей имеют объекты 10 и 11(12 связей), а меньше всего 1 и 2(1 и 2 связи соответственно). Что говорит о том, что 1 и 2 объекты аномальны.

Разбиение древа осуществляется путем выбора пороговой величины h. В данном случае она равна 0,435(получаются «нормальные» плеяды). Значит, удаляем все связи больше данного числа. В результате получаем «нормальные» плеяды(рис 3,9):

 

 

Рис.3,9 «Нормальные» плеяды.

Замечание: периодизация с помощью метода корреляционных плеяд выделила точно такие же периоды развития, что и периодизация с помощью метода дендритов.

Тогда названия периодов будут аналогичными:

I период 1997,1998 – выше среднего уровень здоровья

II период 1993-1995  - средний уровень здоровья

III период 1996,1999–ниже среднего уровень здоровья

IV период 2000-2005 –критический или низкий  уровень здоровья

А интерпретация получается следующая I период –это низкое здоровье населения но для России это максимально достигнутое значение за рассматриваемый период(1991-2005) и тому подобное.

 

Заключение.

Периодизация – разбиение динамических рядов на интервалы однокачественного развития.

Периодизация, с одной стороны, дает важную информацию о процессе, с другой- закладывает основы для последующего анализа динамики, так как обеспечивает возможность применения методов многомерной статистики; адекватное их использование возможно лишь в однородных сферах. Однако, в отличие от типологической группировки, периодизация исключительно редко используется в расчетах, соответственно и теория ее применения практически не разработана, нет устоявшихся корректных статистических методов ее реализации. Причин данной ситуации несколько, и основная заключается в противоречивости различных условий применения алгоритмов корреляционно-регрессионного анализа(КРА) в рядах динамики.

Однородными периодами примято считать временной промежуток, соответствующий одной из следующих ситуаций: равенство уровней ряда; равенство абсолютных приростов; равенство вторых абсолютных разностей;

равенство цепных темпов роста.

 

Прежде чем прибегнуть к помощи методов сравнительного анализа, необходимо выполнить определенные преобразования: составить матрицу наблюдений, стандартизовать или нормировать данных, рассчитать матрицу расстояний или матрицу коэффициентов корреляции.

Недостатком метода шаров является то, что существует потенциальная возможность разделить действительно однородные объекты(однородность это структурное сходство).

Положительной чертой методов дендрита и корреляционных плеяд является их относительная простота. Но самым большим достоинством этих двух методов является инвариантность их техники относительно характера исходных данных. Эти методы успешно реализуются как на различных метриках в случае использования метода дендритов, так и на матрицах коэффициентов взаимной сопряженности, либо на теоретико- информационных мер связи в том случае, если будет применен метод корреляционных плеяд. Более того , как техника метода дендритов применима к матрицам связи, так и метод корреляционных плеяд можно реализовать на матрицах расстояний.

Преимуществом также метода корреляционных плеяд является то, что он учитывает все связи он не отбрасывает как два предыдущих метода «не нужную информацию».

Недостатком методов(особенно корреляционных плеяд) является их неформализованность, что затрудняет применение вычислительной техники, т.е он становится очень трудоемким при достаточно большом числе объектов.

Изменение уровня здоровья в России в основном протекает в рамках очень низких показателей, что может  привести к еще более сильному ухудшению здоровья. Стоит надеяться на то, что нацпроект здоровье, принятый 21 декабря 2005 года, изменит эту ситуацию.

Можно также отметить, что все методы периодизации выделили два аномальных, переходных года 1991 и 1992.Метод корреляционных плеяд наглядно показал на сколько сильно взаимосвязаны объекты данной совокупности(древо взаимосвязей).

Используя эти методы, мы всегда можем получить информацию об однородности числовых данных, определенных локальных сгущениях и разреженности. Благодаря этим методам можно выяснить, каким образом размещаются точки объекты в многомерном пространстве их взаимосвязи.

Исследования в данной тематике будут продолжаться , так как данные методы несут эмпирический характер.

 

 

 

Список литературы.

 

1) Плюта В: Сравнительный многомерный анализ в экономических исследованиях: Методы таксономии и факторного анализа/ Пер. с пол. В.В. Иванова; Науч. ред. В.М. Жуковский . – М .: Статистика, 1980. – 151с.

2) Плюта В: Сравнительный многомерный анализ в экономическом моделировании/ Пер. с польск. В.В. Иванова. – М .: Финансы и статистика, 1989. – 175с.

3) Глинский В.В. Статистические методы прогнозирования социально-экономических процессов.- Новосибирск,1992. 42 с.

4) Аркадьев А.Г., Браверман Э.М. Обучение машин классификации объектов. М., Наука,1971,192с.

5) Статистика: учебное пособие/ И.Г. Переяслова, Е.Б. Колбачев, О.Г. Переяслова. – изд.2-е.- Ростов н/Д.:Феникс,2005. -282 с.

6) Афанасьев В.Н., Юзбашев М.М. Анализ временных рядов и прогнозирование: учебник.- М.: Финансы и статистика,2001. -228 с.

7) Глинский В.В., Ионин И.Г. Статистический анализ: учебное пособие. 3-е изд., пепераб. И доп. – М.:ИНФРА-М; Новосибирск: Сибирское соглашение,2002.- 241с.

8) Дубров А.М., Мхиторян В.С., Трошин Л.И. Многомерные статистические методы : Учебник. – М.: Финансы и статистика, 1998. -352с.

9) Статистический словарь 1996г. Москва. Фмнстатинформ. Главный редактор Юрков Ю.А.

10) Российский статистический ежегодник 2006: Стат.сб/ Росстат.-М., 2006. 806 с.

11) Российский статистический ежегодник: Стат.сб/ Госкомстат России.- М.,2001. – 679 с.

12) Россия в цифрах. 2007: Крат. Стат. Сб/ Росстат – М., 2007,-494с.

 

[1]