 |
Главная |
Описание метода Ньютона (метода касательных)
|
из
5.00
|
Пусть корень  уравнения f ( x ) = 0 отделён на отрезке, причем f ’( x ) и f ’’( x ) непрерывны и сохраняют определённые знаки при
уравнения f ( x ) = 0 отделён на отрезке, причем f ’( x ) и f ’’( x ) непрерывны и сохраняют определённые знаки при  . Найдя какое-нибудь n-e приближение корня
. Найдя какое-нибудь n-e приближение корня  n
n  (
(  ), мы можем уточнить его по Методу Ньютона следующим образом. Пусть
), мы можем уточнить его по Методу Ньютона следующим образом. Пусть  , где hn малая величина. Отсюда, применяя формулу Тейлора, получим:
, где hn малая величина. Отсюда, применяя формулу Тейлора, получим:

Следовательно,

Внеся эту поправку в формулу (2), получим следующее по порядку приближение корня:
 (n=0,1,2…).
(n=0,1,2…).
Геометрически метод Ньютона эквивалентен замене небольшой дуги кривой y = f ( x ) касательной, проведенной в некоторой точке кривой. в самом деле, положим для определённости, что f ’’( x )>0 при  и f ( b )>0 (рис. 1).
и f ( b )>0 (рис. 1).
Выберем, например, х0=b, для которого f ( x ) f ’’( x )>0. Проведем касательную к кривой y = f ( x ) в точке B0 (x0, f(x0)).

В качестве 1-го приближения x 1 корня  возьмем абсциссу точки пересечения этой касательной с осью Ox . Через точку B1( x 1, f ( x 1)) снова проведем касательную, абсцисса точки пересечения которой с Ox даст нам 2-е приближение x 2 корня
возьмем абсциссу точки пересечения этой касательной с осью Ox . Через точку B1( x 1, f ( x 1)) снова проведем касательную, абсцисса точки пересечения которой с Ox даст нам 2-е приближение x 2 корня  и т.д. (рис. 1). Очевидно, что уравнение касательной в точке Bn (xn, f ( xn)) (где n=0,1,2…) есть
и т.д. (рис. 1). Очевидно, что уравнение касательной в точке Bn (xn, f ( xn)) (где n=0,1,2…) есть

Полагая, что у=0, x = xn +1,получим формулу (3):
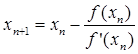 .
.
Заметим, что если в нашем случае положить х0=a и, следовательно, f ( x ) f ’’( x )<0, то, проведя касательную к кривой y = f ( x )в точке A ( a , f ( a )) , мы получили бы точку x1’ (рис. 1), лежащую вне отрезка [а, b], т. е. при этом выборе начального значения метод Ньютона оказывается непрактичным. Таким образом, в данном случае «хорошим» начальным приближением х0 является то, для которого выполнено неравенство
 (4)
(4)
Докажем, что это правило является общим.
Теорема. Если f(a)f(b)<0, причем f'(x) и f" (х) отличны от нуля и сохраняют определенные знаки при  , то, исходя из начального приближения удовлетворяющего неравенству (4), можно вычислить методом Ньютона (формула (3)) единственный корень
, то, исходя из начального приближения удовлетворяющего неравенству (4), можно вычислить методом Ньютона (формула (3)) единственный корень  уравнения (1) с любой степенью точности.
уравнения (1) с любой степенью точности.
Доказательство. Пусть, например, f(a)< 0, f(b)>0, f '(x) >0, f ’’( x )>0 при  (остальные случаи рассматриваются аналогично). Согласно неравенству (4) имеем f(x0) >0 (например, можно принять х0 = b).
(остальные случаи рассматриваются аналогично). Согласно неравенству (4) имеем f(x0) >0 (например, можно принять х0 = b).
Методом математической индукции докажем, что все приближения xn>  (n = 0, 1, 2,...) и, следовательно, f ( xn )>0. В самом деле, прежде всего, x0 >
(n = 0, 1, 2,...) и, следовательно, f ( xn )>0. В самом деле, прежде всего, x0 >  .
.
Пусть теперь xn>  . Положим
. Положим

Применяя формулу Тейлора, получим:

где  <cn<xn.
<cn<xn.
Так как f ’’( x )>0, то имеем:

и, следовательно,

что и требовалось доказать.
Из формулы (3), учитывая знаки f(xn) и f’(х n ), имеем хn+1 < хn (n = 0, 1, ...), т. е. последовательные приближения x0, x1,…, хn, ... образуют ограниченную монотонно убывающую последовательность. Следовательно, существует  .
.
Переходя к пределу в равенстве (3), будем иметь:

т.е. f (  )=0. Следовательно,
)=0. Следовательно,  =
=  , что и требовалось доказать.
, что и требовалось доказать.
Поэтому, применяя метод Ньютона, следует руководствоваться следующим правилом: в качестве исходной точки х0 выбирается тот конец интервала (а, b ), которому отвечает ордината того же знака, что и знак f"(x).
Замечание 1. Если:
1. функция f ( x ) определена и непрерывна при  ;
;
2. f (a)f(b)<0;
3. f’(x)  при
при  ;
;
4. f "(x) существует всюду и сохраняет постоянный знак, то при применении метода Ньютона для нахождения корня уравнения f ( x ) = 0, лежащего в интервале (а, b ), за начальное приближение x0 можно принять любое значение  . В частности, можно взять x 0= a или x 0= b.
. В частности, можно взять x 0= a или x 0= b.
Действительно, пусть, например, f ’( x ) > 0 при  , f"(x )>0 и х0 = с, где
, f"(x )>0 и х0 = с, где 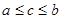 .
.
Если f (с) = 0, то корень  = с и задача, таким образом, решена.
= с и задача, таким образом, решена.
Если f ( c ) > 0, то справедливо приведенное выше рассуждение и процесс Ньютона с начальным значением с сходится к корню  .
.
Наконец, если f (с) <0, то находим значение

Применяя формулу Тейлора, будем иметь:

где  —некоторое промежуточное значение между с и х1. Таким образом, f ( x 1) f ’’( x 1)>0.
—некоторое промежуточное значение между с и х1. Таким образом, f ( x 1) f ’’( x 1)>0.
Кроме того, из условия f"(x) >0 вытекает, что f ’ (х) — возрастающая функция и, значит, f ’( x ) > f ' (а) > 0 при х>а. Следовательно, х1 можно принять за начальное значение для процесса Ньютона, сходящегося к некоторому корню 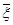 функции f ( x ) такому, что
функции f ( x ) такому, что  > с
> с  а. Так как в силу положительности производной f ' (х) при х > а функция f ( x ) имеет единственный корень на интервале (а, +
а. Так как в силу положительности производной f ' (х) при х > а функция f ( x ) имеет единственный корень на интервале (а, +  ), то
), то 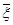 =
=  .
.
Аналогичное рассмотрение можно провести для других комбинаций знаков производных f ’( x )и f"(x).
Замечание 2. Из формулы (3) видно, что чем больше численное значение производной f ’( x ) в окрестности данного корня, тем меньше поправка, которую нужно прибавить к n-му приближению, чтобы получить (n+l)-e приближение. Поэтому метод Ньютона особенно удобно применять тогда, когда в окрестности данного корня график функции имеет большую крутизну. Но если численное значение производной f ’( x ) близ корня мало, то поправки будут велики, и вычисление корня по этому методу может оказаться очень долгим, а иногда и вовсе невозможным. Следовательно, если кривая y = f ( x ) вблизи точки пересечения с осью Ох почти горизонтальна, то применять метод Ньютона для решения уравнения f ( x ) = 0 не рекомендуется.
Оценка погрешности
Для оценки погрешности n-го приближения хn можно воспользоваться общей формулой.
 (6)
(6)
где m1 — наименьшее значение | f ’( x )|на отрезке [а, b].
Выведем еще одну формулу для оценки точности приближения xn. Применяя формулу Тейлора, имеем:
 (7)
(7)
где  . Так как в силу определения приближения хп имеем
. Так как в силу определения приближения хп имеем

то из (7) находим:

где М2 — наибольшее значение | f " (х)|на отрезке [а, b].Следовательно, на основании формулы (6) окончательно получаем:
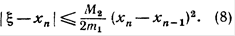
Если процесс Ньютона сходится, то хп- хп-1 0 при п—►  . Поэтому при п
. Поэтому при п  имеем:
имеем:

т.е. «установившиеся» начальные десятичные знаки приближений xn -1 и xn начиная с некоторого приближения, являются верными.
Заметим, что в общем случае совпадение с точностью до е двух последовательных приближений хп-1 и хп вовсе не гарантирует, что с той же точностью совпадает значение хп и точный корень | (рис. 19).
Установим также формулу, связывающую абсолютные погрешности двух последовательных приближений хп и xn +1. Из формулы (5) получаем:

где 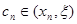 . Отсюда, учитывая формулу (3), будем иметь:
. Отсюда, учитывая формулу (3), будем иметь:

и, следовательно,
 (9)
(9)
Формула (9) обеспечивает быструю сходимость процесса Ньютона, если начальное приближение х0 таково, что

В частности, если

то из формулы (9) получаем:

т.е. в этом случае, если приближение хп имело m верных десятичных знаков после запятой, то следующее приближение хп+1 будет иметь по меньшей мере 2т верных знаков; иными словами, если  , то с помощью метода Ньютона число верных знаков после запятой искомого корня
, то с помощью метода Ньютона число верных знаков после запятой искомого корня  удваивается на каждом шаге.
удваивается на каждом шаге.

|
из
5.00
|
Обсуждение в статье: Описание метода Ньютона (метода касательных) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

