 |
Главная |
Метод хорд (линейной аппроксимации)
|
из
5.00
|
Информация о предыдущих приближениях корня используется для нахождения последующих приближений не только в методе касательных. В качестве примера другого такого метода мы приведём метод, основанный на нахождении xi + 1 по двум предыдущим приближениям xi и xi − 1 с помощью линейной интерполяции, называемый методом хорд.
Идея метода состоит в том, что по двум точкам Mi − 1(xi − 1;f(xi − 1)) и Mi(xi;f(xi)) построить прямую Mi − 1Mi (то есть хорду, соединяющую две точки графика y = f(x)) и взять в качестве следующего приближения xi + 1 абсциссу точки пересечения этой прямой с осью Ox. Иными словами, приближённо заменить на этом шаге функцию f(x) её линейной интерполяцией, найденной по двум значениям : x и xi − 1. (Линейной интерполяцией функции f(x) назовём такую линейную функцию  , значения которой совпадают со значениями f(x) в двух фиксированных точках, в данном случае -- в точках xi − 1 и xi.)
, значения которой совпадают со значениями f(x) в двух фиксированных точках, в данном случае -- в точках xi − 1 и xi.)
Уравнение хорды - это уравнение прямой, проходящей через две точки (a, f(a)) и (b, f(b)).
В зависимости от того, лежат ли точки xi − 1 и xi по разные стороны от корня x * или же по одну и ту же сторону, получаем такие чертежи:

Рис 3. Построение последовательного приближения по методу хорд: два случая.
Итак, очередное последовательное приближение будет зависеть от двух предыдущих:  . Найдём выражение для функции
. Найдём выражение для функции  .
.
Интерполяционную линейную функцию  будем искать как функцию с угловым коэффициентом, равным разностному отношению
будем искать как функцию с угловым коэффициентом, равным разностному отношению

построенному для отрезка между xi − 1 и xi, график которой проходит через точку Mi:

Решая уравнение  , находим
, находим
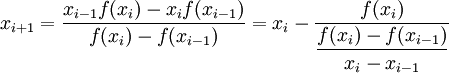
то есть
 (1)
(1)
Заметим, что величина ki может рассматриваться как разностное приближение для производной f'(x) в точке xi. Тем самым полученная формула (1) -- это разностный аналог итерационной формулы метода Ньютона. Вычисление по формуле (1) гораздо предпочтительнее вычисления по другой полученной нами формуле

хотя эти две формулы математически тождественны, поскольку при использовании формулы (1) в случае вычислений с округлениями (например, на компьютере) достигается меньшая потеря значащих цифр.
Погрешность
Имеются две разновидности применения формулы (1). Первая разновидность: вычисления ведутся непосредственно по формуле (1) при 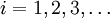 , начиная с двух приближений x0 и x1, взятых, по возможности, поближе к корню x * . При этом не предполагается, что x * лежит между x0 и x1 (и что значения функции f в точках x0 и x1 имеют разные знаки). При этом не гарантируется, что корень попадёт на отрезок между xi − 1 и xi на каком-либо следующем шаге (хотя это и исключено). В таком случае затруднительно дать оценку погрешности, с которой xi + 1 приближает истинное значение корня x * , и поэтому довольствуются таким эмпирическим правилом: вычисления прекращают, когда будет выполнено неравенство
, начиная с двух приближений x0 и x1, взятых, по возможности, поближе к корню x * . При этом не предполагается, что x * лежит между x0 и x1 (и что значения функции f в точках x0 и x1 имеют разные знаки). При этом не гарантируется, что корень попадёт на отрезок между xi − 1 и xi на каком-либо следующем шаге (хотя это и исключено). В таком случае затруднительно дать оценку погрешности, с которой xi + 1 приближает истинное значение корня x * , и поэтому довольствуются таким эмпирическим правилом: вычисления прекращают, когда будет выполнено неравенство  , где
, где  - желаемая точность нахождения корня. При этом полагают приближённое значение корня равным
- желаемая точность нахождения корня. При этом полагают приближённое значение корня равным  .
.
Условие сходимости
Достаточное условие сходимости, таково: 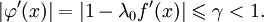 Это неравенство может быть переписано в виде
Это неравенство может быть переписано в виде 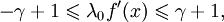 откуда получаем, что сходимость гарантируется, когда, во-первых,
откуда получаем, что сходимость гарантируется, когда, во-первых,  так как
так как  (тем самым проясняется смысл выбора знака числа
(тем самым проясняется смысл выбора знака числа  ), а во-вторых, когда
), а во-вторых, когда  при всех X на всём рассматриваемом отрезке, окружающем корень. Это второе неравенство заведомо выполнено, если
при всех X на всём рассматриваемом отрезке, окружающем корень. Это второе неравенство заведомо выполнено, если

где  . Таким образом, угловой коэффициент K не должен быть слишком мал по абсолютной величине: при малом угловом коэффициенте уже на первом шаге точка X[1] может выскочить из рассматриваемой окрестности корня X[*] , и сходимость итераций к корню может быть нарушена.
. Таким образом, угловой коэффициент K не должен быть слишком мал по абсолютной величине: при малом угловом коэффициенте уже на первом шаге точка X[1] может выскочить из рассматриваемой окрестности корня X[*] , и сходимость итераций к корню может быть нарушена.
|
из
5.00
|
Обсуждение в статье: Метод хорд (линейной аппроксимации) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

