 |
Главная |
К решению номера 4 контрольной работы номер 1 .
|
из
5.00
|
.
Определение . Если в линейном пространстве 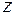 существует
существует 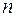 линейно независимых векторов, а любые
линейно независимых векторов, а любые 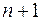 векторов линейно зависимы, то линейное пространство
векторов линейно зависимы, то линейное пространство 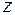 называется
называется 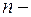 мерным. Число
мерным. Число 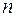 называется размерностью пространства и обозначается
называется размерностью пространства и обозначается 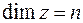 .
.
Определение. Если 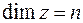 , то система из
, то система из 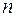 линейно независимых векторов
линейно независимых векторов 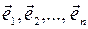 , заданных в определенном порядке, называется базисом пространства
, заданных в определенном порядке, называется базисом пространства 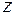 .
.
Теорема. Если 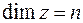 ,
, 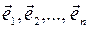 - базис в
- базис в 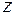 , то любой вектор
, то любой вектор 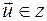 можно единственным образом разложить по базису, т.е. представить в виде линейной комбинации базисных векторов:
можно единственным образом разложить по базису, т.е. представить в виде линейной комбинации базисных векторов: 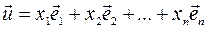 ,
, 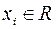 .
.
Определение . Будем говорить, что три вектора 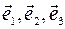 в трехмерном пространстве
в трехмерном пространстве 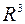 образуют ортонормированный базис, если длина каждого из них равна единице и они попарно ортогональны,
образуют ортонормированный базис, если длина каждого из них равна единице и они попарно ортогональны,
Т.е. 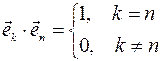 ,
, 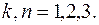

К решению номера 5 контрольной работы номер 1(вариант 1)
Ненулевой вектор 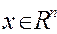 называется собственным вектором линейного оператора
называется собственным вектором линейного оператора  , если существует такое число
, если существует такое число 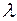 , что выполняется равенство:
, что выполняется равенство: 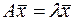 . Число
. Число 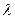 называется собственным значением оператора
называется собственным значением оператора 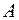 , отвечающим собственному вектору
, отвечающим собственному вектору 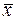 .
.
Множество собственных значений линейного оператора называется его спектром.
Рассмотрим матрицу оператора в некотором базисе:
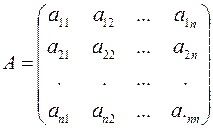
Тогда соотношение 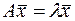 или (
или ( 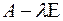 ),
), 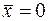 эквивалентно следующему:
эквивалентно следующему:
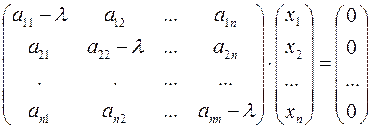

Это есть однородная система 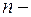 ого порядка, всегда имеющая нулевое решение
ого порядка, всегда имеющая нулевое решение 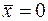 . По правилу Крамера она будет иметь ненулевые решения тогда и только тогда, когда ее определитель равен нулю, т.е.
. По правилу Крамера она будет иметь ненулевые решения тогда и только тогда, когда ее определитель равен нулю, т.е.
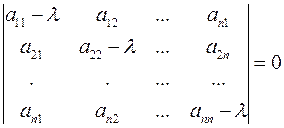 (1)
(1)
Итак, собственные числа 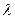 являются корнями алгебраического уравнения
являются корнями алгебраического уравнения 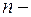 ого порядка (1), которое называется характеристическими уравнением, а его левая часть - характеристическим многочленом.
ого порядка (1), которое называется характеристическими уравнением, а его левая часть - характеристическим многочленом.
Заметим, что собственные значения не зависят от выбора базиса, в котором записывается матрица оператора 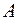 .
.
Пусть 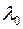 - собственное значение, т.е. решение характеристического уравнения (1). Тогда собственный вектор
- собственное значение, т.е. решение характеристического уравнения (1). Тогда собственный вектор 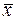 , отвечающий этому собственному значению, будет решением однородной системы
, отвечающий этому собственному значению, будет решением однородной системы
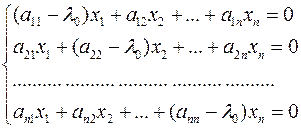 (2)
(2)
Так как множество решений линейной однородной системы является линейным пространством, то для нахождения собственных векторов  , отвечающих собственному значению
, отвечающих собственному значению 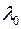 , достаточно найти базис этого пространства.
, достаточно найти базис этого пространства.
Пример. Найти собственные векторы и собственные значения линейного оператора 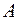 с матрицей
с матрицей
A= 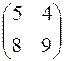
Решение. Составим характеристическое уравнение (1):
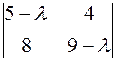 =0 или
=0 или 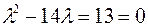
Собственные значения: 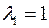 ;
; 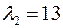 . Для
. Для 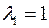 составим систему (2):
составим систему (2):
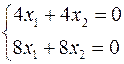 ~
~ 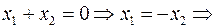

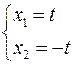
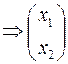 =
= 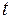
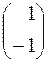 -одномерное линейное пространство собственных векторов с базисом
-одномерное линейное пространство собственных векторов с базисом 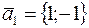 .
.
Для 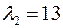
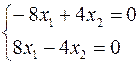 ~
~ 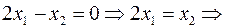
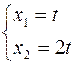
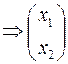 =
= 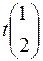 -одномерное линейное пространство
-одномерное линейное пространство
собственных векторов с базисом 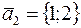 .
.
Отметим, что векторы 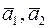 в
в 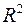 образуют базис
образуют базис 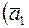 не параллельно
не параллельно  . Так как
. Так как 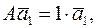
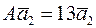 , то матрица линейного оператора в том базисе будет диагональной:
, то матрица линейного оператора в том базисе будет диагональной:
А= 
К решению номера 5.(вариант 2)
Приведение квадратичной формы к каноническому виду.
Если квадратичная форма такова, что все 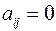 при
при 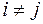 , то она называется квадратичной формой канонического вида. Очевидно, что матрица квадратичной формы является диагональной; будем квадратичную форму канонического вида записывать так:
, то она называется квадратичной формой канонического вида. Очевидно, что матрица квадратичной формы является диагональной; будем квадратичную форму канонического вида записывать так:
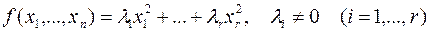
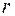 - ранг квадратичной формы;
- ранг квадратичной формы; 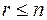 .
.
Теорема. Пусть 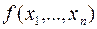 - произвольная квадратичная форма от
- произвольная квадратичная форма от 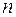 переменных. Тогда найдется такое линейное невырожденное преобразование переменных, которое эту форму приведет к каноническому виду.
переменных. Тогда найдется такое линейное невырожденное преобразование переменных, которое эту форму приведет к каноническому виду.
Сформулируем правило приведения квадратичной формы к каноническому виду. Рассмотри два возможных случая.
1) Существует хотя бы одно  . Пусть, например,
. Пусть, например, 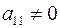 . Выделим в квадратичной форме группу членов, содержащих
. Выделим в квадратичной форме группу членов, содержащих 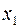 и дополним ее до полного квадрата, тогда получим:
и дополним ее до полного квадрата, тогда получим:
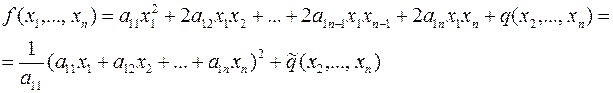
Здесь 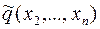 есть квадратичная форма, полученная в результате приведения подобных членов из
есть квадратичная форма, полученная в результате приведения подобных членов из 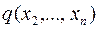 и членов, появившихся в результате выделения полного квадрата;
и членов, появившихся в результате выделения полного квадрата; 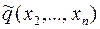 уже не зависит от
уже не зависит от 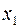 . Можно применить линейное преобразование:
. Можно применить линейное преобразование: 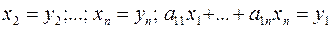 ,
,
Получим: 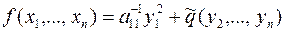 .
.
Если при этом квадратичная форма содержит хотя бы один квадрат, с ней поступают аналогично; в итоге получим сумму квадратов (канонический вид). Каждому выделению полного квадрата будет соответствовать невырожденное линейное преобразование переменных. Произведение всех этих преобразований, приводящим данную квадратичную форму к каноническому виду.
2) Пусть теперь все 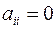 ; значит хотя бы один из
; значит хотя бы один из 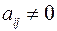 при
при 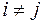 . Пусть
. Пусть 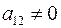 . Тогда нужно сделать преобразование переменных
. Тогда нужно сделать преобразование переменных 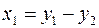 ;
; 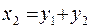 ;
; 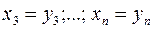 , в результате которого получим квадратичную форму, содержащую квадрат переменного, т.е. первый случай.
, в результате которого получим квадратичную форму, содержащую квадрат переменного, т.е. первый случай.
Пример. Привести квадратичную форму к каноническому виду 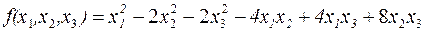 .
.
Решение. Группу подчеркнутых членов можно записать в виде:

Подставляя их в данную квадратичную форму и приводя подобные слагаемые, получаем
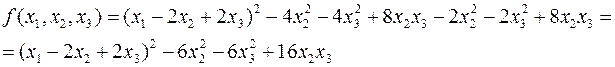
Теперь рассмотрим группу членов 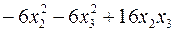
Проведем в ней выкладки, аналогичные выше приведенным, т.е.
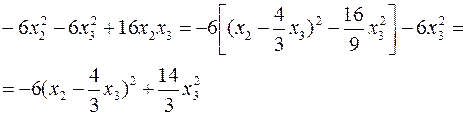
Таким образом, данную квадратичную форму можно записать в виде:
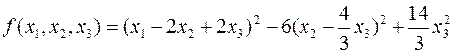
Введем новые переменные:
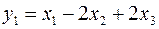 ;
; 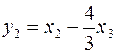 ;
; 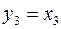 или
или
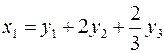 ;
; 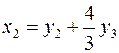 ;
; 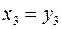
Последние равенства задают линейное преобразование переменных, которое приводит данную квадратичную форму к каноническому виду:
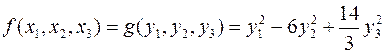 .
.
Приведение действительной квадратичной формы к каноническому виду.
Будем рассматривать только действительные квадратичные формы. Действительное линейное преобразование неизвестных (2) называется ортогональным, если оно сумму квадратов неизвестных 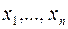 переводит в сумму квадратов
переводит в сумму квадратов 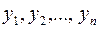 . Матрица
. Матрица 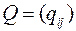 этого преобразования называется ортогональной.
этого преобразования называется ортогональной.
Для приведения действительной квадратичной формы к каноническому виду можно использовать теоремы:
1. Всякая действительная квадратичная форма 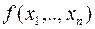 некоторым ортогональным преобразованием неизвестных может быть приведена к каноническому виду.
некоторым ортогональным преобразованием неизвестных может быть приведена к каноническому виду.
2. Каково бы ни было ортогональное преобразование неизвестных, приводящее к каноническому виду квадратичную форму 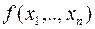 с матрицей
с матрицей 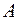 , коэффициентами этого канонического вида являются характеристические корни матрицы
, коэффициентами этого канонического вида являются характеристические корни матрицы 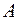 , взятые с их кратностями.
, взятые с их кратностями.
Таким образом, чтобы записать канонический вид квадратичной формы 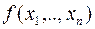 с матрицей
с матрицей 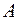 , к которому она приводится посредством ортогонального преобразования неизвестных, согласно теореме 2 достаточно найти корни многочлена
, к которому она приводится посредством ортогонального преобразования неизвестных, согласно теореме 2 достаточно найти корни многочлена 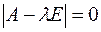
Если
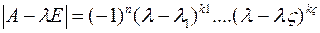
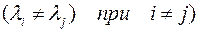 , то ее канонический вид с точностью до нумерации неизвестных следующий:
, то ее канонический вид с точностью до нумерации неизвестных следующий:
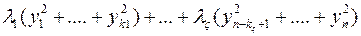
Пример. Найти канонический вид, к которому приводится квадратичная форма  посредствам ортогонального преобразования неизвестных, не находя этого преобразования.
посредствам ортогонального преобразования неизвестных, не находя этого преобразования.
Решение. 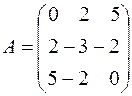
ее характеристический многочлен
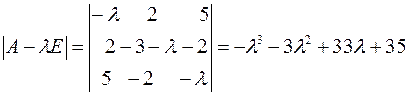
Имеет корни: 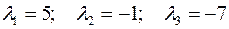 . Тогда запишем канонический вид квадратичной формы:
. Тогда запишем канонический вид квадратичной формы: 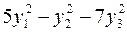 .
.
Чтобы найти матрицу 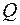 - матрицу искомого ортогонального преобразования, необходимо относительно
- матрицу искомого ортогонального преобразования, необходимо относительно 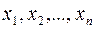 решить систему для каждого корня
решить систему для каждого корня 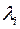 :
:
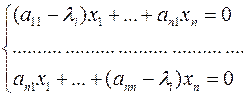 (5)
(5)
Получим систему решений, подвергнем ее процессу ортогонализации и нормирования, получим систему координатных строк, которые составляют матрицу 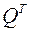 , по ней находим
, по ней находим 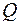 .
.
Пример. Для квадратичной формы 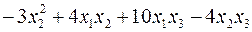 найти ортогональное преобразование, приводящее ее каноническому виду.
найти ортогональное преобразование, приводящее ее каноническому виду.
Решение. Канонический вид этой формы найден выше; собственные значения имеют вид: 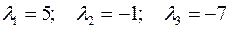 .
.
Составляем систему (5):
1) 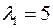
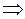
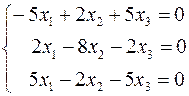
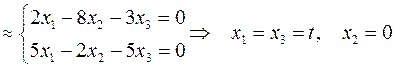
Т.е. получился вектор 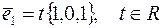 .
.
2) 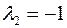
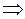
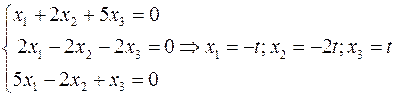
Т.е. получился вектор 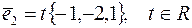 .
.
3) 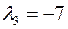
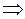
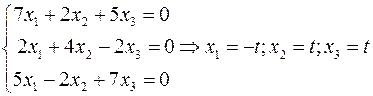
Т.е. получился вектор 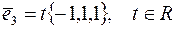 .
.
Векторы 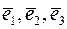 взаимно ортогональны при любых
взаимно ортогональны при любых 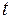 . Нормируем эти векторы при
. Нормируем эти векторы при 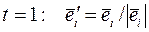
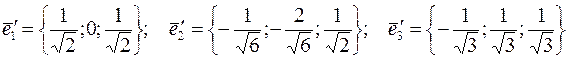
Следовательно,
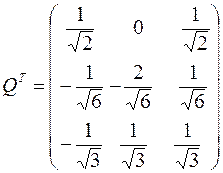
Тогда

Искомое преобразование неизвестных имеет вид:
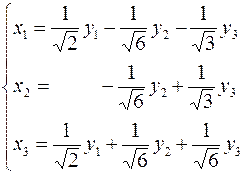
|
из
5.00
|
Обсуждение в статье: К решению номера 4 контрольной работы номер 1 . |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

