 |
Главная |
Ранг матрицы и его вычисление.
|
из
5.00
|
Тульский филиал
Кафедра «Математика и информатика»
УЧЕБНО-МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ
Для решения контрольной работы номер 2
По дисциплине
МАТЕМАТИКА
Для студентов 1 курса, обучающихся по
Направлению 38.03.01 «Экономика»
(программа подготовки бакалавра)
К.ф.-м.н., доцент
Васина М.В.
К.ф.-м.н., доцент
Манохин Е.В.
Утвержден на заседании
Кафедры «Математика и информатика»
Протокол 1 от 28.08.2015 г.
Тула 2015

К решению номера 1 контрольной работы номер 1 .
Произведение матриц.
Определение 5. Произведением матрицы  на матрицу
на матрицу  называется матрица
называется матрица 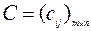 размера
размера  , элементы которой определяются равенствами
, элементы которой определяются равенствами  .
.
Число столбцов в первой матрице должно совпадать с числом строк во второй.
Например.
 ;
; 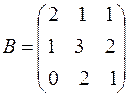 ;
;  ,
,
Т.к.

Т.е. произведение матриц не обладает коммутативностью.
Транспонирование матрицы.
Определение . Транспонированием матрицы  называется замена строк этой матрицы ее столбцами с сохранением их номера.
называется замена строк этой матрицы ее столбцами с сохранением их номера.
Полученная матрица обозначается  .
.
Например.
 .
.
Определитель (число) квадратной матрицы порядка 
 обозначается символами:
обозначается символами:
 .
.
Определение . Алгебраическим дополнением  элемента
элемента  называется определитель
называется определитель  порядка, полученный из
порядка, полученный из  вычеркиванием
вычеркиванием  строки и
строки и  столбца, на пересечении которых стоит элемент
столбца, на пересечении которых стоит элемент  , взятый со знаком
, взятый со знаком 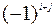 .
.
Например.

Определитель 
 - го порядка равен
- го порядка равен  .
.
Такое разложение называется разложением по элементам первой строки. Оно сводит вычисление  - го порядка к вычислению определителей
- го порядка к вычислению определителей  - го порядка и т.д., до определителей 2-го порядка.
- го порядка и т.д., до определителей 2-го порядка.
Можно доказать, что определитель можно вычислить путем разложения по любой строке или столбцу. Например, разлагая по 1-ой строке, получим:
 .
.
Определение . Минором 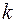 - ого порядка матрицы
- ого порядка матрицы  называется определитель, составленный из элементов, расположенных на пересечении каких – либо
называется определитель, составленный из элементов, расположенных на пересечении каких – либо 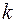 строк и
строк и 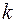 столбцов (
столбцов (  ).
).
Обратная матрица.
Определение 10. Если  - квадратная матрица и матрица
- квадратная матрица и матрица  такая, что
такая, что  (
(  - единичная), то она называется обратной для
- единичная), то она называется обратной для  и обозначается
и обозначается  .
.
Таким образом, по определению,  .
.
Теорема. Для того, чтобы квадратная матрица  имела обратную, необходимо и достаточно, чтобы
имела обратную, необходимо и достаточно, чтобы  .
.
Алгоритм нахождения  сводится к следующему:
сводится к следующему:
1) составляется вспомогательная матрица  из алгебраических дополнений
из алгебраических дополнений  и определителя
и определителя  :
:

2) полученная матрица транспонируется:

Используя разложение определителя по строке, легко убедится, что  - обратная для
- обратная для  .
.
Пример. Найти обратную матрицу для 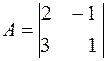 .
.
Решение.
 ;
;
 =
= 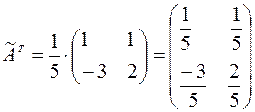 .
.
Ранг матрицы и его вычисление.
Рангом матрицы  называется наибольший порядок минора этой матрицы, отличного от нуля. Всякий отличный от нуля минор, порядок которого равен рангу этой матрицы, называется базисным минором. Ранг матрицы будем обозначать через
называется наибольший порядок минора этой матрицы, отличного от нуля. Всякий отличный от нуля минор, порядок которого равен рангу этой матрицы, называется базисным минором. Ранг матрицы будем обозначать через  ;
;  означает, что матрица имеет минор порядка
означает, что матрица имеет минор порядка  , отличный от нуля, а все миноры порядка
, отличный от нуля, а все миноры порядка  или равны нулю или не существуют.
или равны нулю или не существуют.
При вычислении ранга матрицы полезно пользоваться элементарными преобразованиями как над строками, так и над столбцами.
Пример. Определить ранг матрицы
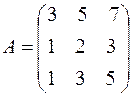
Поменять местами первую и вторую строки:

 .
.
Ко второй строке прибавим первую, умноженную на (-3), и к первой прибавим третью, умноженную на (-1):


Вычтем из третьей строки вторую:

Ранг последней матрицы равен 2, т.к.

 .
.
|
из
5.00
|
Обсуждение в статье: Ранг матрицы и его вычисление. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

